Question Number 41461 by rahul 19 last updated on 07/Aug/18
$$\mathrm{Find}\:\mathrm{area}\:\mathrm{of}\:\mathrm{square}\:\mathrm{inserted}\:\mathrm{in}\:\mathrm{curve} \\ $$$$\mathrm{f}\left({x}\right)=\:\mathrm{3}{x}−{x}^{\mathrm{3}} . \\ $$
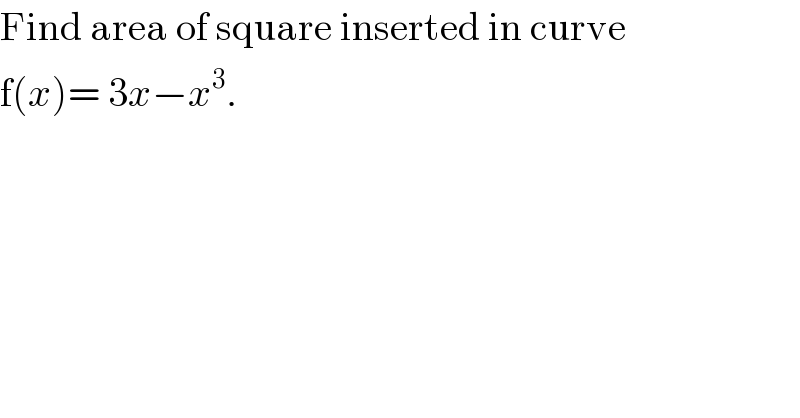
Commented by rahul 19 last updated on 07/Aug/18
Commented by rahul 19 last updated on 07/Aug/18
$$\mathrm{Ans}:\:\left(\mathrm{216}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(−\mathrm{108}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} . \\ $$
Commented by MJS last updated on 07/Aug/18
$$\mathrm{216}^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{6} \\ $$$$\left(−\mathrm{108}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =−\mathrm{108}^{\frac{\mathrm{1}}{\mathrm{3}}} =−\left(\mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} =−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{answer}=\mathrm{6}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$
Answered by MJS last updated on 07/Aug/18
![idea: intersect y=d with f(x) we don′t need x_1 <0 solve x_3 −x_2 =d for d 3x−x^3 =d x^3 −3x+d=0 [f′(x)=3−3x^2 ⇒ max(f(x))= ((1),(2) ) ⇒ ⇒ 0<d<2 ⇔ x_1 , x_2 , x_3 ∈R ⇒ ⇒ we need the trigonometric method] x_1 =−2sin((1/3)(π+arcsin (d/2))) x_2 =2sin((1/3)arcsin (d/2)) x_3 =2cos((1/3)((π/2)+arcsin (d/2))) x_3 −x_2 =d 2(√3)cos((1/3)(π+arcsin (d/2)))=d (1/3)(π+arcsin (d/2))=arccos (d(√3)/6) π+arcsin (d/2)=3arccos (d(√3)/6) tan(π+arcsin (d/2))=tan(3arccos (d(√3)/6)) (d/(√(4−d^2 )))=(((d^2 −3)(√(12−d^2 )))/(d(d^2 −9))) this leads to d^6 −18d^4 +108d^2 −108=0 d=(√u) u^3 −18u^2 +108u−108=0 u=v+6 v^3 +108=0 v=−3(4)^(1/3) u=6−3(4)^(1/3) d=(√(6−3(4)^(1/3) ))≈1.11256 area of square=d^2 =6−3(4)^(1/3) ≈1.23780](Q41469.png)
$$\mathrm{idea}:\:\mathrm{intersect}\:{y}={d}\:\mathrm{with}\:{f}\left({x}\right) \\ $$$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:{x}_{\mathrm{1}} <\mathrm{0} \\ $$$$\mathrm{solve}\:{x}_{\mathrm{3}} −{x}_{\mathrm{2}} ={d}\:\mathrm{for}\:{d} \\ $$$$ \\ $$$$\mathrm{3}{x}−{x}^{\mathrm{3}} ={d} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}+{d}=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{f}'\left({x}\right)=\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{max}\left({f}\left({x}\right)\right)=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{pmatrix}\:\Rightarrow\right. \\ $$$$\:\:\:\:\:\:\Rightarrow\:\mathrm{0}<{d}<\mathrm{2}\:\Leftrightarrow\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} \:\in\mathbb{R}\:\Rightarrow \\ $$$$\left.\:\:\:\:\:\:\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method}\right] \\ $$$${x}_{\mathrm{1}} =−\mathrm{2sin}\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right)\right) \\ $$$${x}_{\mathrm{2}} =\mathrm{2sin}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right) \\ $$$${x}_{\mathrm{3}} =\mathrm{2cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{2}}+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right)\right) \\ $$$${x}_{\mathrm{3}} −{x}_{\mathrm{2}} ={d} \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right)\right)={d} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right)=\mathrm{arccos}\:\frac{{d}\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\pi+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}=\mathrm{3arccos}\:\frac{{d}\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\mathrm{tan}\left(\pi+\mathrm{arcsin}\:\frac{{d}}{\mathrm{2}}\right)=\mathrm{tan}\left(\mathrm{3arccos}\:\frac{{d}\sqrt{\mathrm{3}}}{\mathrm{6}}\right) \\ $$$$\frac{{d}}{\sqrt{\mathrm{4}−{d}^{\mathrm{2}} }}=\frac{\left({d}^{\mathrm{2}} −\mathrm{3}\right)\sqrt{\mathrm{12}−{d}^{\mathrm{2}} }}{{d}\left({d}^{\mathrm{2}} −\mathrm{9}\right)} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${d}^{\mathrm{6}} −\mathrm{18}{d}^{\mathrm{4}} +\mathrm{108}{d}^{\mathrm{2}} −\mathrm{108}=\mathrm{0} \\ $$$${d}=\sqrt{{u}} \\ $$$${u}^{\mathrm{3}} −\mathrm{18}{u}^{\mathrm{2}} +\mathrm{108}{u}−\mathrm{108}=\mathrm{0} \\ $$$${u}={v}+\mathrm{6} \\ $$$${v}^{\mathrm{3}} +\mathrm{108}=\mathrm{0} \\ $$$${v}=−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$$${u}=\mathrm{6}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$$${d}=\sqrt{\mathrm{6}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}}\approx\mathrm{1}.\mathrm{11256} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{square}={d}^{\mathrm{2}} =\mathrm{6}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}\approx\mathrm{1}.\mathrm{23780} \\ $$