Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 41487 by behi83417@gmail.com last updated on 08/Aug/18

Commented by maxmathsup by imad last updated on 08/Aug/18

2) we have I = ∫ (dx/((1+x)(√((x+(1/2))^2 +(3/4))))) changement x+(1/2) =((√3)/2)sh(t) give I = ∫ (1/((1+((√3)/2)sh(t)−(1/2))((√3)/2)ch(t)))((√3)/2)ch(t)dt =∫ (dt/((1/2) +((√3)/2)sh(t))) = ∫ ((2dt)/((√3)((e^t −e^(−t) )/2) +(1/2))) = ∫ ((4dt)/((√3)e^t −(√3)e^(−t) +1)) =_(e^t =u) ∫ (4/((√3)u−(√3)(1/u)+1)) (du/u) = ∫ ((4du)/((√3)u^2 −(√3) +u)) let decompose F(u) = (4/((√3)u^2 +u−(√3))) we have Δ =1−4(−3)=13 ⇒ u_1 =((−1+(√(13)))/(2(√3))) and u_2 =((−1−(√(13)))/(2(√3))) ⇒F(u) =(4/((√3)(u−u_1 )(u−u_2 ))) =(a/(u−u_1 )) +(b/(u−u_2 )) a = (4/((√3)(u_1 −u_2 ))) = (4/((√3)((√(13))/(√3)))) = (4/(√3)) b = (4/((√3)(u_2 −u_1 ))) =−(4/(√3)) ⇒ F(u) = (4/((√3)(u−u_1 )))−(4/((√3)(u−u_2 ))) ⇒ ∫ F(u)du = (4/(√3))ln∣u−u_1 ∣ −(4/(√3))ln∣u−u_2 ∣ +c =(4/(√3))ln∣ e^t −u_1 ∣ −(4/(√3))ln∣e^t −u_2 ∣ +c but t =argsh(((2x+1)/(√3))) =ln( ((2x+1)/(√3)) +(√(1+(((2x+1)/(√3)))^2 )) ⇒ I = (4/(√3))ln∣ ((2x+1)/(√3)) +(√(1+(((2x+1)/2))^2 ))−u_1 ∣ −(4/(√3))ln∣((2x+1)/(√3)) +(√(1+(((2x+1)/(√3)))^2 )) −u_2 ∣ +c

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{I}\:=\:\int\:\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}}\:\:{changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\int\:\:\:\:\:\:\:\:\:\:\:\frac{{dt}}{\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)}\:=\:\int\:\:\:\frac{\mathrm{2}{dt}}{\sqrt{\mathrm{3}}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}}\:=\:\int\:\:\:\:\frac{\mathrm{4}{dt}}{\sqrt{\mathrm{3}}{e}^{{t}} \:−\sqrt{\mathrm{3}}{e}^{−{t}} \:+\mathrm{1}} \\ $$$$=_{{e}^{{t}} \:={u}} \:\:\:\:\int\:\:\:\:\:\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}{u}−\sqrt{\mathrm{3}}\frac{\mathrm{1}}{{u}}+\mathrm{1}}\:\frac{{du}}{{u}}\:\:=\:\int\:\:\:\:\:\frac{\mathrm{4}{du}}{\sqrt{\mathrm{3}}{u}^{\mathrm{2}} −\sqrt{\mathrm{3}}\:+{u}}\:\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:+{u}−\sqrt{\mathrm{3}}}\:\:\:\:\:{we}\:{have}\:\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{3}\right)=\mathrm{13}\:\Rightarrow \\ $$$${u}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{and}\:{u}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{13}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\:\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)} \\ $$$$=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} } \\ $$$${a}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\left({u}_{\mathrm{1}} −{u}_{\mathrm{2}} \right)}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\frac{\sqrt{\mathrm{13}}}{\sqrt{\mathrm{3}}}}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}} \\ $$$${b}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\left({u}_{\mathrm{2}} −{u}_{\mathrm{1}} \right)}\:=−\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}\:\Rightarrow\:{F}\left({u}\right)\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\left({u}−{u}_{\mathrm{1}} \right)}−\frac{\mathrm{4}}{\sqrt{\mathrm{3}}\left({u}−{u}_{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\int\:\:{F}\left({u}\right){du}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid{u}−{u}_{\mathrm{1}} \mid\:−\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid{u}−{u}_{\mathrm{2}} \mid\:+{c} \\ $$$$=\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\:{e}^{{t}} −{u}_{\mathrm{1}} \mid\:−\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid{e}^{{t}} −{u}_{\mathrm{2}} \mid\:+{c}\:\:{but}\:{t}\:={argsh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$={ln}\left(\:\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:\:\Rightarrow\right. \\ $$$${I}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\:\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−{u}_{\mathrm{1}} \mid\:−\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:−{u}_{\mathrm{2}} \mid\:+{c} \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 08/Aug/18

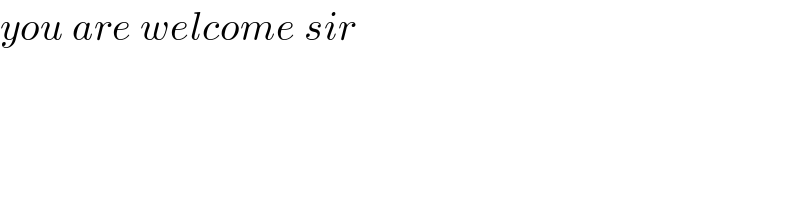
you are welcome sir

$${you}\:{are}\:{welcome}\:{sir} \\ $$

Commented by behi83417@gmail.com last updated on 08/Aug/18

thank you dear proph. abdo.

$${thank}\:{you}\:{dear}\:{proph}.\:{abdo}. \\ $$

Commented by math khazana by abdo last updated on 10/Aug/18

1) let use the changement (√((1+x^2 )/(1−x^2 )))=t ⇒ ((1+x^2 )/(1−x^2 )) =t^2 ⇒ 1+x^2 =t^2 −t^2 x^2 ⇒(1+t^2 )x^2 =t^2 −1⇒ x^2 =((t^2 −1)/(t^2 +1)) ⇒2xdx = ((2t(t^2 +1)−2t(t^2 −1))/((t^2 +1)^2 )) = ((4t)/((t^2 +1)^2 )) dt ⇒ ∫ (1/x)(√((1+x^2 )/(1−x^2 )))dx = ∫ (1/(2x^2 ))(√((1+x^2 )/(1−x^2 ))) (2x)dx = (1/2) ∫ ((t^2 +1)/(t^2 −1)) .t. ((4t)/((t^2 +1)^2 )) dt = ∫ ((2t^2 )/((t^2 −1)(t^2 +1))) dt let decompose F(t) = ((2t^2 )/((t^2 −1)(t^2 +1))) =((2t^2 )/((t−1)(t+1)(t^2 +1))) F(t) = (a/(t−1)) +(b/(t+1)) +((ct +d)/(t^2 +1)) a =lim_(t→1) (t−1)F(t) = (2/4) =(1/2) b =lim_(t→−1) (t+1)F(t) = (2/(−4)) =−(1/2) ⇒ F(t)= (1/(2(t−1))) −(1/(2(t+1))) +((ct +d)/(t^2 +1)) lim_(t→+∞) t F(t) =0 =c ⇒ F(t) =(1/(2(t−1))) −(1/(2(t+1))) +(d/(t^2 +1)) F(0) =−(1/2) −(1/2) +d =0 ⇒d=1 ⇒ F(t)=(1/(2(t−1))) −(1/(2(t+1))) +(1/(t^2 +1)) I =∫ F(t)dt = (1/2)ln∣((t−1)/(t+1))∣ +arctan(t)+c =(1/2)ln∣ (((√((1+x^2 )/(1−x^2 )))−1)/((√((1+x^2 )/(1−x^2 )))+1))∣ +arctan((√((1+x^2 )/(1−x^2 )))) +c .

$$\left.\mathrm{1}\right)\:{let}\:{use}\:{the}\:{changement}\:\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}={t}\:\Rightarrow \\ $$$$\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:\:={t}^{\mathrm{2}} \:\Rightarrow\:\mathrm{1}+{x}^{\mathrm{2}} ={t}^{\mathrm{2}} \:−{t}^{\mathrm{2}} {x}^{\mathrm{2}} \:\:\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}^{\mathrm{2}} ={t}^{\mathrm{2}} \:−\mathrm{1}\Rightarrow \\ $$$${x}^{\mathrm{2}} \:=\frac{{t}^{\mathrm{2}} \:−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:\Rightarrow\mathrm{2}{xdx}\:=\:\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{2}{t}\left({t}^{\mathrm{2}} \:−\mathrm{1}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\Rightarrow \\ $$$$\:\int\:\:\:\frac{\mathrm{1}}{{x}}\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:=\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:\left(\mathrm{2}{x}\right){dx} \\ $$$$=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\int\:\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{2}} \:−\mathrm{1}}\:.{t}.\:\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{dt} \\ $$$$=\:\int\:\:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} \:−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{dt}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{2}{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{2}{t}^{\mathrm{2}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)\:=\:\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{b}}{{t}+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{1}} \left({t}−\mathrm{1}\right){F}\left({t}\right)\:=\:\frac{\mathrm{2}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\:\frac{\mathrm{2}}{−\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}\:={c}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:+\frac{{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:+{d}\:=\mathrm{0}\:\Rightarrow{d}=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${I}\:\:=\int\:\:{F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+{arctan}\left({t}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\:\:\frac{\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}−\mathrm{1}}{\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}+\mathrm{1}}\mid\:+{arctan}\left(\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\:+{c}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 08/Aug/18

2)1+x=(1/t) dx=−(1/t^2 )dt ∫((−dt)/(t^2 ×(1/t)×(√(1+((1/t)−1)+((1/t)−1)^2 )))) ∫((−dt)/(t×(√((1/t)+(1/t^2 )−(2/t)+1)))) ∫((−dt)/(t×(√((t+1−2t+t^2 )/t^2 )))) ∫((−dt)/(√(t^2 −t+1))) ∫((−dt)/(√(t^2 −2.t.(1/2)+(1/4)+1−(1/4)))) ∫((−dt)/(√((t−(1/2))^2 +(((√3)/2))^2 ))) =−ln{(t−(1/2))+(√((t−(1/2))^2 +(((√3)/2))^2 )) =−ln{(1+x−(1/2))+(√((1+x−(1/2))^2 +(3/4))) =−ln{(x+(1/2))+(√(x^2 +x+1)) }+c

$$\left.\mathrm{2}\right)\mathrm{1}+{x}=\frac{\mathrm{1}}{{t}}\:\:{dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}×\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)+\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\int\frac{−{dt}}{{t}×\sqrt{\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{2}}{{t}}+\mathrm{1}}} \\ $$$$\int\frac{−{dt}}{{t}×\sqrt{\frac{{t}+\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} }}} \\ $$$$\int\frac{−{dt}}{\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{1}}} \\ $$$$\int\frac{−{dt}}{\sqrt{{t}^{\mathrm{2}} −\mathrm{2}.{t}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$$\int\frac{−{dt}}{\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=−{ln}\left\{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:}\right. \\ $$$$=−{ln}\left\{\left(\mathrm{1}+{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left(\mathrm{1}+{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\right. \\ $$$$=−{ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\:\right\}+{c} \\ $$$$ \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 08/Aug/18

thank you very much dear tanmay sir.

$${thank}\:{you}\:{very}\:{much}\:{dear}\:{tanmay}\:{sir}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 08/Aug/18

thank you sir...for keeping our mind busy...

$${thank}\:{you}\:{sir}...{for}\:{keeping}\:{our}\:{mind}\:{busy}... \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 08/Aug/18

thanks.I enjoy to see different questions ,iedas, and solutions. I alwyes have good sense and time when being in this forum. thanks to all my best friends and colleagues here. God bless all of you.

$${thanks}.{I}\:{enjoy}\:{to}\:{see}\:{different} \\ $$$${questions}\:,{iedas},\:{and}\:{solutions}. \\ $$$${I}\:{alwyes}\:{have}\:{good}\:{sense}\:{and}\:{time} \\ $$$${when}\:{being}\:{in}\:{this}\:{forum}. \\ $$$${thanks}\:{to}\:{all}\:{my}\:{best}\:{friends}\: \\ $$$${and}\:{colleagues}\:{here}. \\ $$$${God}\:{bless}\:{all}\:{of}\:{you}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 08/Aug/18

1)∫(1/x).(√((1+x^2 )/(1−x^2 ))) dx ∫(1/x).(√((1+x^2 )/(1−x^2 ))) dx t^2 =((1+x^2 )/(1−x^2 )) 1+x^2 =t^2 −t^2 x^2 x^2 (1+t^2 )=t^2 −1 x^2 =((t^2 −1)/(t^2 +1)) 2xdx=(((t^2 +1)2t−(t^2 −1)(2t))/((t^2 +1)^2 ))dt 2xdx=((2t^3 +2t−2t^3 +2t)/((t^2 +1)^2 ))dt xdx=((2tdt)/((t^2 +1)^2 )) ∫(1/x).(√((1+x^2 )/(1−x^2 ))) dx ∫(√((1+x^2 )/(1−x^2 ))) .((xdx)/x^2 ) ∫t.((2tdt)/((t^2 +1)^2 )).((t^2 +1)/(t^2 −1)) ∫((2t^2 )/((t^2 +1)(t^2 −1)))dt ∫((t^2 +1+t^2 −1)/((t^2 +1)(t^2 −1)))dt ∫(dt/(t^2 −1))+∫(dt/(t^2 +1)) =(1/2)∫(((t+1)−(t−1))/((t+1)(t−1)))dt+∫(dt/(t^2 +1)) =(1/2)[∫(dt/(t−1))−∫(dt/(t+1))]−∫(dt/(t^2 +1)) =(1/2)ln(((t−1)/(t+1)))−tan^(−1) (t)+c =(1/2)ln((((√((1+x^2 )/(1−x^2 ))) −1)/((√((1+x^2 )/(1−x^2 ))) +1)))−tan^(−1) ((√((1+x^2 )/(1−x^(2 ) ))) )+c =(1/2)ln((((√(1+x^2 )) −(√(1−x^2 )) )/((√(1+x^2 )) +(√(1−x^2 )) )))−tan^(−1) ((√((1+x^2 )/(1−x^2 ))) )+c

$$\left.\mathrm{1}\right)\int\frac{\mathrm{1}}{{x}}.\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\int\frac{\mathrm{1}}{{x}}.\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:{dx} \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} ={t}^{\mathrm{2}} −{t}^{\mathrm{2}} {x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)={t}^{\mathrm{2}} −\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{2}{xdx}=\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{2}{t}−\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{t}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$\mathrm{2}{xdx}=\frac{\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$${xdx}=\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{1}}{{x}}.\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\int\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:.\frac{{xdx}}{{x}^{\mathrm{2}} } \\ $$$$\int{t}.\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }.\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\int\frac{\mathrm{2}{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$$\int\frac{{t}^{\mathrm{2}} +\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}+\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}+\mathrm{1}\right)−\left({t}−\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)}{dt}+\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{dt}}{{t}−\mathrm{1}}−\int\frac{{dt}}{{t}+\mathrm{1}}\right]−\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)−{tan}^{−\mathrm{1}} \left({t}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:−\mathrm{1}}{\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:+\mathrm{1}}\right)−{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}\:} }}\:\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:}\right)−{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:\right)+{c} \\ $$

Commented by behi83417@gmail.com last updated on 08/Aug/18

nice work.thanks in advance sir.

$${nice}\:{work}.{thanks}\:{in}\:{advance}\:{sir}. \\ $$

Commented by behi83417@gmail.com last updated on 09/Aug/18

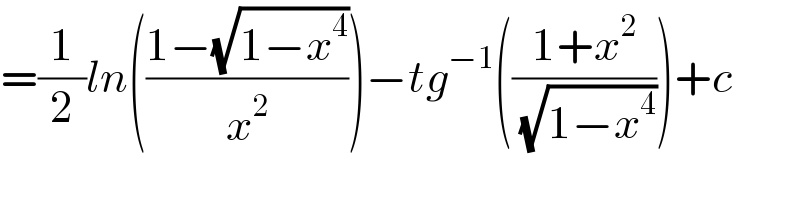
=(1/2)ln(((1−(√(1−x^4 )))/x^2 ))−tg^(−1) (((1+x^2 )/(√(1−x^4 ))))+c

$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{{x}^{\mathrm{2}} }\right)−{tg}^{−\mathrm{1}} \left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\right)+{c} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18

thank you sir...

$${thank}\:{you}\:{sir}... \\ $$

Answered by Ar Brandon last updated on 28/Jul/20

I=∫(dx/((1+x)(√(1+x+x^2 ))))=∫(dx/((x+(1/2)+(1/2))(√((x+(1/2))^2 +(3/4))))) x+(1/2)=((√3)/2)tanθ ⇒dx=((√3)/2)sec^2 θdθ ⇒I=∫((((√3)/2)sec^2 θ dθ)/((((√3)/2)tanθ+(1/2))(√((3/4)tan^2 θ+(3/4))))) =∫((secθ dθ)/(((√3)/2)tanθ+(1/2)))=∫(dθ/(((√3)/2)sinθ+(1/2)cosθ)) =∫(dθ/(sin(π/3)sinθ+cos(π/3)cosθ))=∫(dθ/(cos(θ−(π/3)))) =∫sec(θ−(π/3))dθ=ln∣sec(θ−(π/3))+tan(θ−(π/3))∣+lnA

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}\theta\:\Rightarrow\mathrm{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\Rightarrow\mathcal{I}=\int\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \theta\:\mathrm{d}\theta}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}\theta+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{3}}{\mathrm{4}}\mathrm{tan}^{\mathrm{2}} \theta+\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$$\:\:\:\:\:\:\:\:=\int\frac{\mathrm{sec}\theta\:\mathrm{d}\theta}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}\theta+\frac{\mathrm{1}}{\mathrm{2}}}=\int\frac{\mathrm{d}\theta}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\theta} \\ $$$$\:\:\:\:\:\:\:\:=\int\frac{\mathrm{d}\theta}{\mathrm{sin}\frac{\pi}{\mathrm{3}}\mathrm{sin}\theta+\mathrm{cos}\frac{\pi}{\mathrm{3}}\mathrm{cos}\theta}=\int\frac{\mathrm{d}\theta}{\mathrm{cos}\left(\theta−\frac{\pi}{\mathrm{3}}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\int\mathrm{sec}\left(\theta−\frac{\pi}{\mathrm{3}}\right)\mathrm{d}\theta=\mathrm{ln}\mid\mathrm{sec}\left(\theta−\frac{\pi}{\mathrm{3}}\right)+\mathrm{tan}\left(\theta−\frac{\pi}{\mathrm{3}}\right)\mid+\mathrm{lnA} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com