Question Number 41515 by maxmathsup by imad last updated on 08/Aug/18
![let f_n (x) =((sin(2(n+1)x))/(sinx)) if x∈]0,(π/2)] and f_n (0)=2(n+1) let u_n = ∫_0 ^(π/2) f_n (x)dx 1) prove that ∀n fromN u_(n+1) −u_n =2(((−1)^(n+1) )/(2n+3)) 2)find lim_(n→+∞) u_n](Q41515.png)
$$\left.{l}\left.{et}\:\:{f}_{{n}} \left({x}\right)\:=\frac{{sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)}{{sinx}}\:{if}\:\:{x}\in\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:{and}\:{f}_{{n}} \left(\mathrm{0}\right)=\mathrm{2}\left({n}+\mathrm{1}\right)\:\:{let} \\ $$$${u}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{f}_{{n}} \left({x}\right){dx} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\:\forall{n}\:{fromN}\:\:{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\mathrm{2}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}} \\ $$$$\left.\mathrm{2}\right){find}\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 12/Aug/18
![1) u_(n+1) −u_n =∫_0 ^(π/2) ((sin(2(n+2)x)−sin(2(n+1)x))/(sinx))dx but sinp−sinq =cos((π/2)−p) +cos((π/2)+q) =2 cos(((π−p+q)/2))cos(((−p−q)/2)) = 2cos((π/2) −((p−q)/2))cos(((p+q)/2))=2sin(((p−q)/2))cos(((p+q)/2)) ⇒ sin(2(n+2)x)−sin(2(n+1)x)=2sin(x)cos((((4n+6)x)/2))⇒ u_(n+1) −u_n =2∫_0 ^(π/2) sin(x)cos((2n+3)x) .(1/(sinx)) dx = 2∫_0 ^(π/2) cos{(2n+3)x}dx =2[(1/(2n +3)) sin{(2n+3)x}]_0 ^(π/2) =(2/(2n+3))sin{(2n+3)(π/2)} =(2/(2n+3)) sin(nπ +2π−(π/2)) =−(2/(2n +3)) sin((π/2) −nπ) =−(2/(2n+3))cos(nπ) =2((−(−1)^n )/(2n+3)) =2(((−1)^(n+1) )/(2n+3)) ⇒ u_(n+1) −u_n =2(((−1)^(n+1) )/(2n+3))](Q41792.png)
$$\left.\mathrm{1}\right)\:{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left(\mathrm{2}\left({n}+\mathrm{2}\right){x}\right)−{sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)}{{sinx}}{dx}\:{but} \\ $$$${sinp}−{sinq}\:={cos}\left(\frac{\pi}{\mathrm{2}}−{p}\right)\:\:+{cos}\left(\frac{\pi}{\mathrm{2}}+{q}\right)\:=\mathrm{2}\:{cos}\left(\frac{\pi−{p}+{q}}{\mathrm{2}}\right){cos}\left(\frac{−{p}−{q}}{\mathrm{2}}\right) \\ $$$$=\:\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{2}}\:−\frac{{p}−{q}}{\mathrm{2}}\right){cos}\left(\frac{{p}+{q}}{\mathrm{2}}\right)=\mathrm{2}{sin}\left(\frac{{p}−{q}}{\mathrm{2}}\right){cos}\left(\frac{{p}+{q}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${sin}\left(\mathrm{2}\left({n}+\mathrm{2}\right){x}\right)−{sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)=\mathrm{2}{sin}\left({x}\right){cos}\left(\frac{\left(\mathrm{4}{n}+\mathrm{6}\right){x}}{\mathrm{2}}\right)\Rightarrow \\ $$$${u}_{{n}+\mathrm{1}} −{u}_{{n}} =\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{sin}\left({x}\right){cos}\left(\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right)\:.\frac{\mathrm{1}}{{sinx}}\:{dx} \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left\{\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right\}{dx}\:=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}{n}\:+\mathrm{3}}\:{sin}\left\{\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right\}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{3}}{sin}\left\{\left(\mathrm{2}{n}+\mathrm{3}\right)\frac{\pi}{\mathrm{2}}\right\}\:=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{3}}\:{sin}\left({n}\pi\:+\mathrm{2}\pi−\frac{\pi}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2}{n}\:+\mathrm{3}}\:{sin}\left(\frac{\pi}{\mathrm{2}}\:−{n}\pi\right)\:=−\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{3}}{cos}\left({n}\pi\right)\:=\mathrm{2}\frac{−\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{3}}\:=\mathrm{2}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}}\:\Rightarrow \\ $$$${u}_{{n}+\mathrm{1}} \:−{u}_{{n}} =\mathrm{2}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 12/Aug/18
$$\left.\mathrm{2}\right)\:{we}\:{have}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({u}_{{k}+\mathrm{1}} \:−{u}_{{k}} \right)\:=\mathrm{2}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{3}}\:\Rightarrow \\ $$$${u}_{{n}} −{u}_{\mathrm{0}} =\:\mathrm{2}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{3}}\:\:\:\left(\:\:\:{j}={k}+\mathrm{1}\right) \\ $$$$=\mathrm{2}\:\sum_{{j}=\mathrm{1}} ^{{n}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{j}} }{\mathrm{2}{j}+\mathrm{1}}\:\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} ={u}_{\mathrm{0}} \:\:+\mathrm{2}\:\sum_{{j}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{j}} }{\mathrm{2}{j}+\mathrm{1}} \\ $$$$=\:{u}_{\mathrm{0}} \:\:+\:\mathrm{2}\sum_{{j}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{j}} }{\mathrm{2}{j}+\mathrm{1}}\:−\mathrm{2}\:={u}_{\mathrm{0}} \:−\mathrm{2}\:+\:\mathrm{2}\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{2}}\:+{u}_{\mathrm{0}} \:−\mathrm{2}\:\:{but} \\ $$$${u}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}\:{dx}\:=\pi\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:\:{u}_{{n}} =\frac{\mathrm{3}\pi}{\mathrm{2}}\:−\mathrm{2}\:. \\ $$
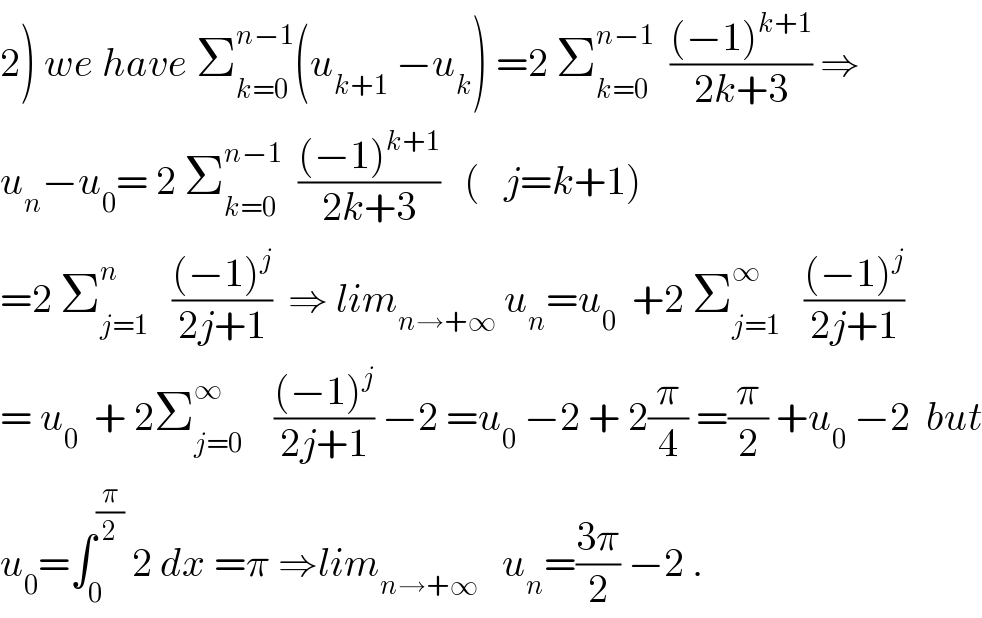
Commented by math khazana by abdo last updated on 13/Aug/18
$${u}_{\mathrm{0}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{{sinx}}\:{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cosx}\:{dx}=\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:\:{u}_{{n}} =\mathrm{2}−\mathrm{2}\:+\frac{\mathrm{2}\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {u}_{{n}} =\frac{\pi}{\mathrm{2}}\:. \\ $$
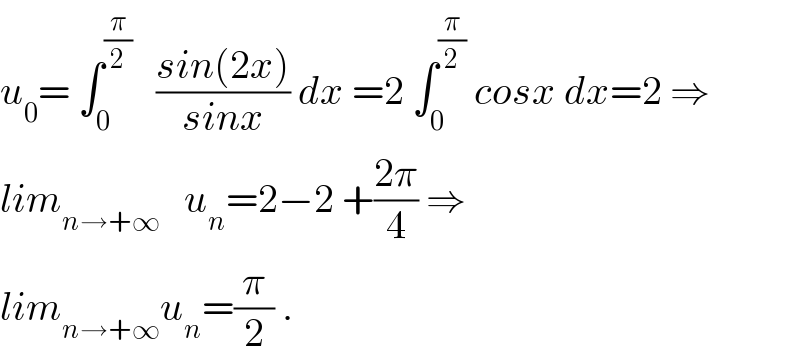
Answered by alex041103 last updated on 10/Aug/18
![We know that: sin(2(n+2)x)=sin(2(n+1)x+2x)= =cos(2x)sin(2(n+1)x)+sin(2x)cos(2(n+1)x) cos(2x)=1−2sin^2 x sin(2x)=2sin(x)cos(x) ⇒u_(n+1) =∫_0 ^(π/2) (((1−2sin^2 x)sin(2(n+1)x))/(sin(x)))dx+∫_0 ^(π/2) ((2sin(x)cos(x)cos(2(n+1)x))/(sin(x)))dx =u_n +2∫_0 ^(π/2) (cos(x)cos(2(n+1)x)−sin(x)sin(2(n+1)x))dx= ⇒u_(n+1) −u_n =2∫cos((2n+3)x)dx= =(2/(2n+3))∫cos((2n+3)x)d((2n+3)x)= =(2/(2n+1))[sin((2n+3)(π/2))−sin(0)] sin((2n+3)(π/2))=sin((n+1)π + (π/2)) sin(t+π)=cos(π)sin(t)+sin(π)cos(t)= =−sin(t) ⇒sin((n+1)π + (π/2))=(−1)^(n+1) sin(π/2)=(−1)^(n+1) ⇒u_(n+1) −u_n =((2(−1)^(n+1) )/(2n+3)) ⇒Σ_(k=0) ^n u_(k+1) −u_k =u_(n+1) −u_0 =2Σ_(k=0) ^n (((−1)^(k+1) )/(2k+3)) u_0 =∫_0 ^(π/2) ((sin(2x))/(sin(x)))dx=2∫_0 ^(π/2) cos(x)dx=2 ⇒u_n =2Σ_(k=−1) ^(n−1) (((−1)^(k+1) )/(2k+3))=2Σ_(k=0−1) ^(n−1) (((−1)^(k+1) )/(2(k+1)+1)) ⇒u_n =Σ_(k=0) ^n ((2(−1)^k )/(2k+1)) lim_(n→∞) u_n =2Σ_(k=0) ^∞ (((−1)^k )/(2k+1))=2(π/4)=(π/2) Ans. u_∞ =π/2](Q41605.png)
$${We}\:{know}\:{that}: \\ $$$${sin}\left(\mathrm{2}\left({n}+\mathrm{2}\right){x}\right)={sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}+\mathrm{2}{x}\right)= \\ $$$$={cos}\left(\mathrm{2}{x}\right){sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)+{sin}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right) \\ $$$${cos}\left(\mathrm{2}{x}\right)=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x} \\ $$$${sin}\left(\mathrm{2}{x}\right)=\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right) \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right){sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)}{{sin}\left({x}\right)}{dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right){cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$={u}_{{n}} +\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cos}\left({x}\right){cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)−{sin}\left({x}\right){sin}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)\right){dx}= \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\mathrm{2}\int{cos}\left(\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right){dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{3}}\int{cos}\left(\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right){d}\left(\left(\mathrm{2}{n}+\mathrm{3}\right){x}\right)= \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\left[{sin}\left(\left(\mathrm{2}{n}+\mathrm{3}\right)\frac{\pi}{\mathrm{2}}\right)−{sin}\left(\mathrm{0}\right)\right] \\ $$$${sin}\left(\left(\mathrm{2}{n}+\mathrm{3}\right)\frac{\pi}{\mathrm{2}}\right)={sin}\left(\left({n}+\mathrm{1}\right)\pi\:+\:\frac{\pi}{\mathrm{2}}\right) \\ $$$${sin}\left({t}+\pi\right)={cos}\left(\pi\right){sin}\left({t}\right)+{sin}\left(\pi\right){cos}\left({t}\right)= \\ $$$$=−{sin}\left({t}\right) \\ $$$$\Rightarrow{sin}\left(\left({n}+\mathrm{1}\right)\pi\:+\:\frac{\pi}{\mathrm{2}}\right)=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {sin}\left(\pi/\mathrm{2}\right)=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{k}+\mathrm{1}} −{u}_{{k}} ={u}_{{n}+\mathrm{1}} −{u}_{\mathrm{0}} =\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{3}} \\ $$$${u}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sin}\left(\mathrm{2}{x}\right)}{{sin}\left({x}\right)}{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {cos}\left({x}\right){dx}=\mathrm{2} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{2}\underset{{k}=−\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{3}}=\mathrm{2}\underset{{k}=\mathrm{0}−\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}\left({k}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$\Rightarrow{u}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\infty} {{lim}u}_{{n}} =\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}=\mathrm{2}\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$$${Ans}.\:{u}_{\infty} =\pi/\mathrm{2} \\ $$