
Question and Answers Forum
Question Number 41516 by maxmathsup by imad last updated on 08/Aug/18
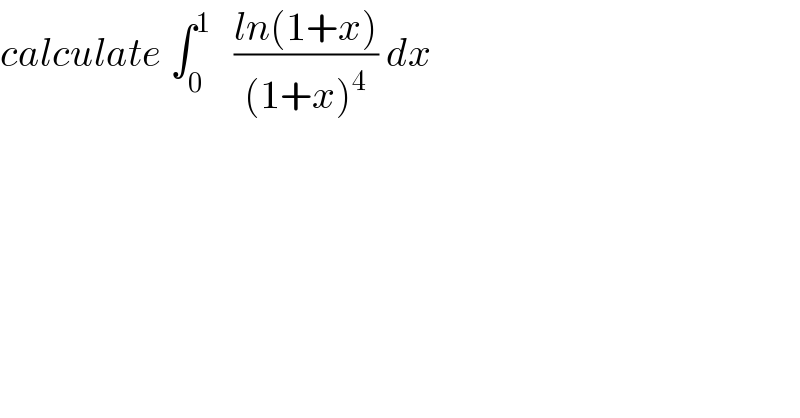
Commented by turbo msup by abdo last updated on 12/Aug/18
![let A =∫_0 ^1 ((ln(1+x))/((1+x)^4 ))dx changement 1+x =t give A = ∫_1 ^2 ((ln(t))/t^4 )dt and by parts u^′ =t^(−4) and v=ln(t) ⇒ A =[−(1/3)t^(−3) ln(t)]_1 ^2 +∫_1 ^2 (1/3) t^(−3) (dt/t) =−(1/3)((ln(2))/8) +(1/3) ∫_1 ^2 t^(−4) dt =−((ln(2))/(24)) +(1/3)[−(1/3)t^(−3) ]_1 ^2 =−((ln(2))/(24)) −(1/9)( (1/8) −1) =−((ln(2))/(24)) −(1/9)(((−7)/8)) =(7/(72)) −((ln(2))/(24))](Q41774.png)
Answered by alex041103 last updated on 09/Aug/18
![∫_0 ^1 ((ln(1+x))/((1+x)^4 )) dx=∫_0 ^1 ((ln(1+x))/((1+x)^4 )) d(x+1)= =∫_1 ^2 ((ln(x))/x^4 ) dx=I let x=e^u ⇒dx=e^u du ⇒I=∫_0 ^( ln(2)) (u/e^(4u) )e^u du=∫_0 ^(ln(2)) ue^(−3u) du= =−(1/3)∫_0 ^(ln(2)) ud(e^(−3u) ) We integrate by parts: −3I=ue^(−3u) ]_0 ^(ln(2)) −∫_0 ^(ln(2)) e^(−3u) du= =((ln(2))/8)−(7/(24)) ⇒I=(7/(72))−((ln(2))/(24))≈0.0683411](Q41548.png)
| ||
Question and Answers Forum | ||
Question Number 41516 by maxmathsup by imad last updated on 08/Aug/18 | ||
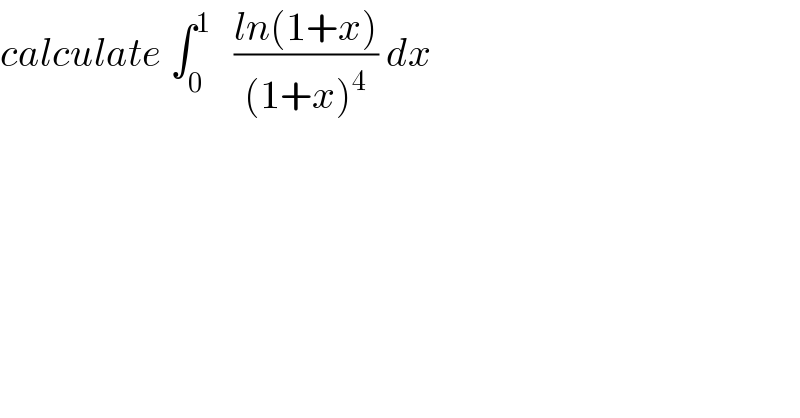 | ||
Commented by turbo msup by abdo last updated on 12/Aug/18 | ||
![let A =∫_0 ^1 ((ln(1+x))/((1+x)^4 ))dx changement 1+x =t give A = ∫_1 ^2 ((ln(t))/t^4 )dt and by parts u^′ =t^(−4) and v=ln(t) ⇒ A =[−(1/3)t^(−3) ln(t)]_1 ^2 +∫_1 ^2 (1/3) t^(−3) (dt/t) =−(1/3)((ln(2))/8) +(1/3) ∫_1 ^2 t^(−4) dt =−((ln(2))/(24)) +(1/3)[−(1/3)t^(−3) ]_1 ^2 =−((ln(2))/(24)) −(1/9)( (1/8) −1) =−((ln(2))/(24)) −(1/9)(((−7)/8)) =(7/(72)) −((ln(2))/(24))](Q41774.png) | ||
Answered by alex041103 last updated on 09/Aug/18 | ||
![∫_0 ^1 ((ln(1+x))/((1+x)^4 )) dx=∫_0 ^1 ((ln(1+x))/((1+x)^4 )) d(x+1)= =∫_1 ^2 ((ln(x))/x^4 ) dx=I let x=e^u ⇒dx=e^u du ⇒I=∫_0 ^( ln(2)) (u/e^(4u) )e^u du=∫_0 ^(ln(2)) ue^(−3u) du= =−(1/3)∫_0 ^(ln(2)) ud(e^(−3u) ) We integrate by parts: −3I=ue^(−3u) ]_0 ^(ln(2)) −∫_0 ^(ln(2)) e^(−3u) du= =((ln(2))/8)−(7/(24)) ⇒I=(7/(72))−((ln(2))/(24))≈0.0683411](Q41548.png) | ||
| ||