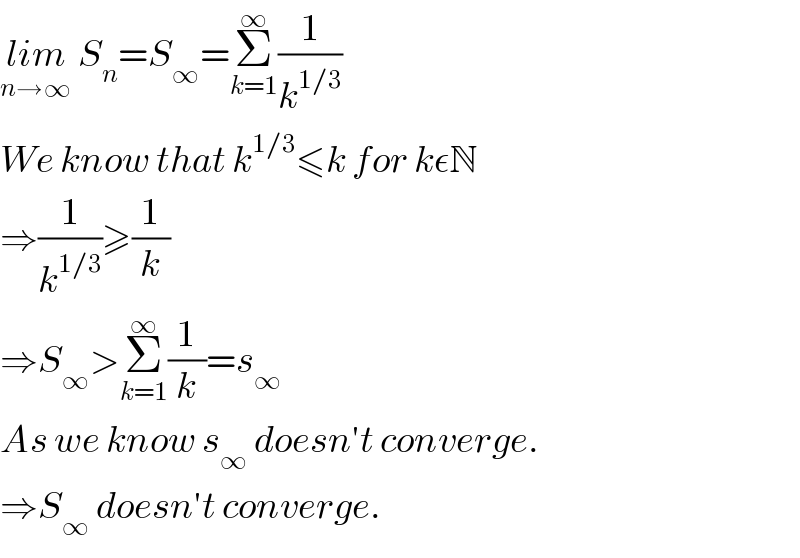let S_n = 1 +(1/((^3 (√2)))) + (1/((^3 (√3)))) + ....+(1/((^3 (√n)))) calculate lim _(n→+∞) S


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 41517 by maxmathsup by imad last updated on 08/Aug/18

$l e t S_{n} = 1 + \frac{1}{(^{3} \sqrt{2})} + \frac{1}{(^{3} \sqrt{3})} + . . . . + \frac{1}{(^{3} \sqrt{n})}$ $c a l c u l a t e l i m_{n \to + \infty} S_{n}$
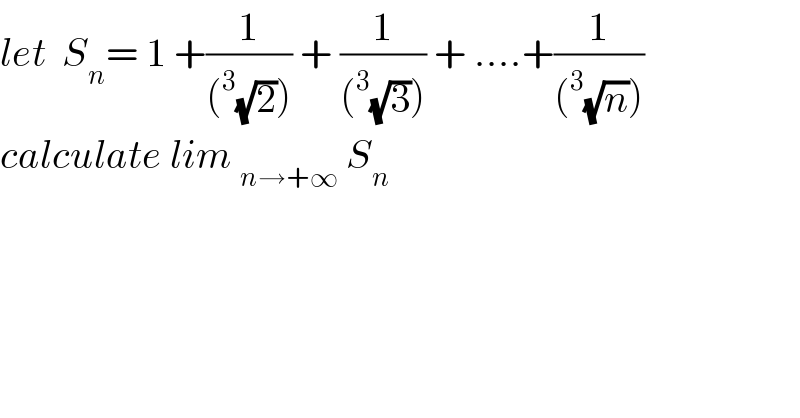
Commented by maxmathsup by imad last updated on 10/Aug/18
$we have S_n =Σ_(k=1) ^n (1/k^(1/3) ) the function t→(1/x^(1/3) ) is decreasing so ∫_k ^(k+1) (dt/t^(1/3) ) ≤ (1/k^(1/3) ) ≤ ∫_(k−1) ^k (dt/t^(1/3) ) ⇒ Σ_(k=2) ^n ∫_k ^(k+1) (dt/t^(1/3) ) ≤ Σ_(k=2) ^n (1/k^(1/3) ) ≤ Σ_(k=2) ^n ∫_(k−1) ^k (dt/t^(1/3) ) ⇒ ∫_2 ^(n+1) t^(−(1/3)) dt ≤ S_n −1 ≤ ∫_1 ^n t^(−(1/3)) dt ⇒ [ (3/2) t^(2/3) ]_2 ^(n+1) ≤ S_n −1 ≤ [ (3/2) t^(2/3) ]_1 ^n ⇒(3/2){ (n+1)^(2/3) −2^(2/3) }≤ S_n −1 ≤ (3/2){ n^(2/3) −1}⇒ S_n ≥ 1 +(3/2)(n+1)^(2/3) −(3/2) 2^(2/3) →+∞(n→+∞) ⇒ lim_(n→+∞) S_n =+∞ .$
$w e h a v e S_{n} = \sum_{k = 1}^{n} \frac{1}{k^{\frac{1}{3}}} t h e f u n c t i o n t \to \frac{1}{x^{\frac{1}{3}}} i s d e c r e a s i n g s o$ $\int_{k}^{k + 1} \frac{d t}{t^{\frac{1}{3}}} ⩽ \frac{1}{k^{\frac{1}{3}}} ⩽ \int_{k - 1}^{k} \frac{d t}{t^{\frac{1}{3}}} \Rightarrow \sum_{k = 2}^{n} \int_{k}^{k + 1} \frac{d t}{t^{\frac{1}{3}}} ⩽ \sum_{k = 2}^{n} \frac{1}{k^{\frac{1}{3}}} ⩽ \sum_{k = 2}^{n} \int_{k - 1}^{k} \frac{d t}{t^{\frac{1}{3}}}$ $\Rightarrow \int_{2}^{n + 1} t^{- \frac{1}{3}} d t ⩽ S_{n} - 1 ⩽ \int_{1}^{n} t^{- \frac{1}{3}} d t \Rightarrow$ ${[\frac{3}{2} t^{\frac{2}{3}}]}_{2}^{n + 1} ⩽ S_{n} - 1 ⩽ {[\frac{3}{2} t^{\frac{2}{3}}]}_{1}^{n} \Rightarrow \frac{3}{2} {{(n + 1)}^{\frac{2}{3}} - 2^{\frac{2}{3}}} ⩽ S_{n} - 1$ $⩽ \frac{3}{2} {n^{\frac{2}{3}} - 1} \Rightarrow S_{n} ⩾ 1 + \frac{3}{2} {(n + 1)}^{\frac{2}{3}} - \frac{3}{2} 2^{\frac{2}{3}} \to + \infty (n \to + \infty) \Rightarrow$ ${l i m}_{n \to + \infty} S_{n} = + \infty .$
	Answered by alex041103 last updated on 09/Aug/18

	$\underset{n \to \infty}{l i m} S_{n} = S_{\infty} = \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{1 / 3}}$ $W e k n o w t h a t k^{1 / 3} ⩽ k f o r k ϵ N$ $\Rightarrow \frac{1}{k^{1 / 3}} ⩾ \frac{1}{k}$ $\Rightarrow S_{\infty} > \underset{k = 1}{\sum^{\infty}} \frac{1}{k} = s_{\infty}$ $A s w e k n o w s_{\infty} {d o e s n}^{'} t c o n v e r g e .$ $\Rightarrow S_{\infty} {d o e s n}^{'} t c o n v e r g e .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum