Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 41627 by alex041103 last updated on 10/Aug/18

Commented by alex041103 last updated on 10/Aug/18

Just for fun! I have already posted this Q. around a year ago. The result is beautiful and worths giving it a try. Can you prove something interesting. Hint: Calculate the result.

$${Just}\:{for}\:{fun}!\:{I}\:{have}\:{already}\:{posted} \\ $$$${this}\:{Q}.\:{around}\:{a}\:{year}\:{ago}.\:{The}\:{result} \\ $$$${is}\:{beautiful}\:{and}\:{worths}\:{giving}\:{it}\:{a}\:{try}. \\ $$$${Can}\:{you}\:{prove}\:{something}\:{interesting}. \\ $$$${Hint}:\:{Calculate}\:{the}\:{result}. \\ $$

Commented by maxmathsup by imad last updated on 10/Aug/18

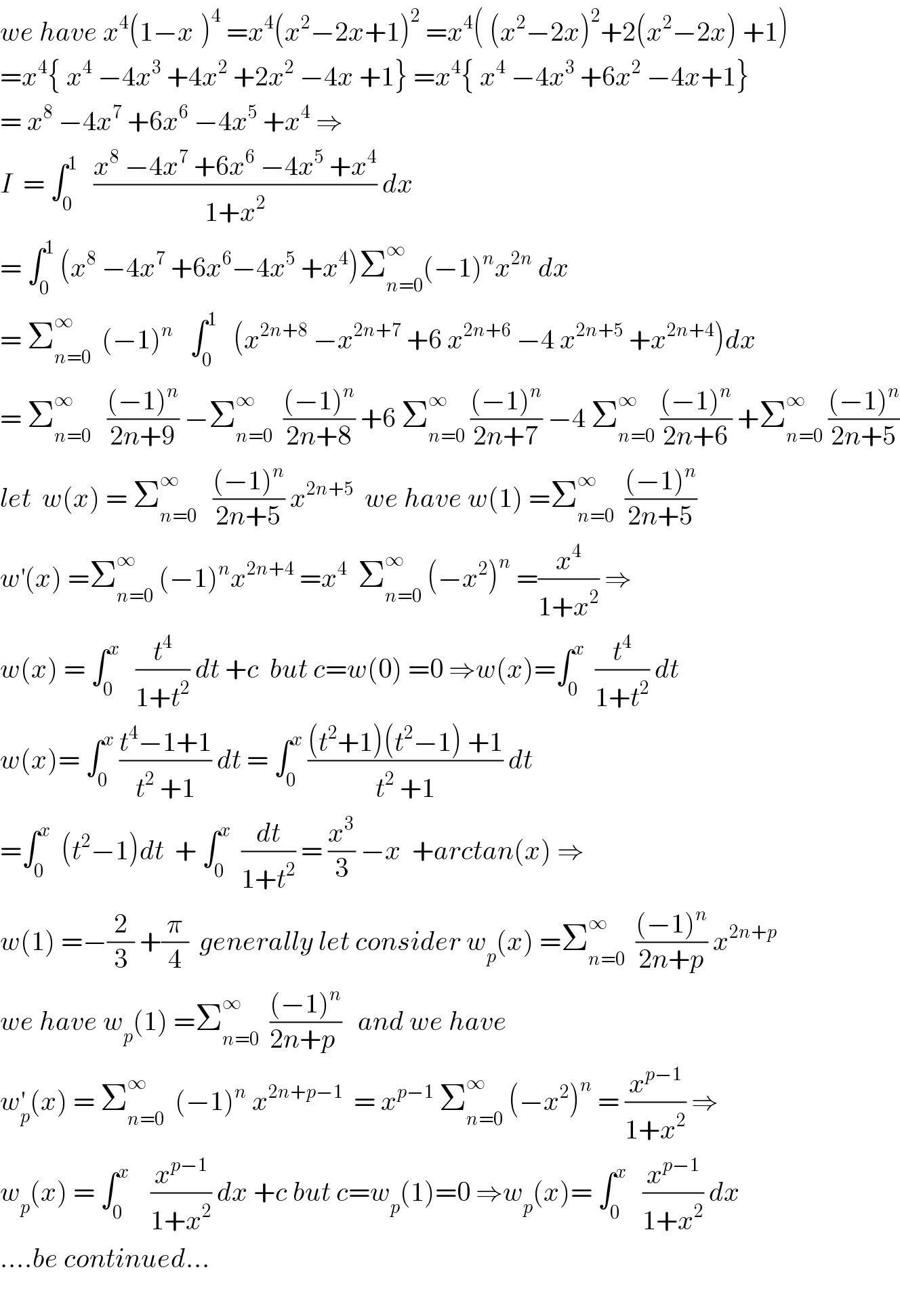
we have x^4 (1−x^ )^4 =x^4 (x^2 −2x+1)^2 =x^4 ( (x^2 −2x)^2 +2(x^2 −2x) +1) =x^4 { x^4 −4x^3 +4x^2 +2x^2 −4x +1} =x^4 { x^4 −4x^3 +6x^2 −4x+1} = x^8 −4x^7 +6x^6 −4x^5 +x^4 ⇒ I = ∫_0 ^1 ((x^8 −4x^7 +6x^6 −4x^5 +x^4 )/(1+x^2 )) dx = ∫_0 ^1 (x^8 −4x^7 +6x^6 −4x^5 +x^4 )Σ_(n=0) ^∞ (−1)^n x^(2n) dx = Σ_(n=0) ^∞ (−1)^(n ) ∫_0 ^1 (x^(2n+8) −x^(2n+7) +6 x^(2n+6) −4 x^(2n+5) +x^(2n+4) )dx = Σ_(n=0) ^∞ (((−1)^n )/(2n+9)) −Σ_(n=0) ^∞ (((−1)^n )/(2n+8)) +6 Σ_(n=0) ^∞ (((−1)^n )/(2n+7)) −4 Σ_(n=0) ^∞ (((−1)^n )/(2n+6)) +Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) let w(x) = Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) x^(2n+5) we have w(1) =Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) w^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(2n+4) =x^4 Σ_(n=0) ^∞ (−x^2 )^n =(x^4 /(1+x^2 )) ⇒ w(x) = ∫_0 ^x (t^4 /(1+t^2 )) dt +c but c=w(0) =0 ⇒w(x)=∫_0 ^x (t^4 /(1+t^2 )) dt w(x)= ∫_0 ^x ((t^4 −1+1)/(t^2 +1)) dt = ∫_0 ^x (((t^2 +1)(t^2 −1) +1)/(t^2 +1)) dt =∫_0 ^x (t^2 −1)dt + ∫_0 ^x (dt/(1+t^2 )) = (x^3 /3) −x +arctan(x) ⇒ w(1) =−(2/3) +(π/4) generally let consider w_p (x) =Σ_(n=0) ^∞ (((−1)^n )/(2n+p)) x^(2n+p) we have w_p (1) =Σ_(n=0) ^∞ (((−1)^n )/(2n+p )) and we have w_p ^′ (x) = Σ_(n=0) ^∞ (−1)^n x^(2n+p−1) = x^(p−1) Σ_(n=0) ^∞ (−x^2 )^n = (x^(p−1) /(1+x^2 )) ⇒ w_p (x) = ∫_0 ^x (x^(p−1) /(1+x^2 )) dx +c but c=w_p (1)=0 ⇒w_p (x)= ∫_0 ^x (x^(p−1) /(1+x^2 )) dx ....be continued...

$${we}\:{have}\:{x}^{\mathrm{4}} \left(\mathrm{1}−{x}^{} \right)^{\mathrm{4}} \:={x}^{\mathrm{4}} \left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:={x}^{\mathrm{4}} \left(\:\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)\:+\mathrm{1}\right) \\ $$$$={x}^{\mathrm{4}} \left\{\:{x}^{\mathrm{4}} \:−\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{2}{x}^{\mathrm{2}} \:−\mathrm{4}{x}\:+\mathrm{1}\right\}\:={x}^{\mathrm{4}} \left\{\:{x}^{\mathrm{4}} \:−\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:−\mathrm{4}{x}+\mathrm{1}\right\} \\ $$$$=\:{x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} \:−\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} \:\Rightarrow \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} \:−\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\: \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} \right)\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \:{dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}\:\:} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\left({x}^{\mathrm{2}{n}+\mathrm{8}} \:−{x}^{\mathrm{2}{n}+\mathrm{7}} \:+\mathrm{6}\:{x}^{\mathrm{2}{n}+\mathrm{6}} \:−\mathrm{4}\:{x}^{\mathrm{2}{n}+\mathrm{5}} \:+{x}^{\mathrm{2}{n}+\mathrm{4}} \right){dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{9}}\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{8}}\:+\mathrm{6}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{7}}\:−\mathrm{4}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{6}}\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}} \\ $$$${let}\:\:{w}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}}\:{x}^{\mathrm{2}{n}+\mathrm{5}} \:\:{we}\:{have}\:{w}\left(\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}} \\ $$$${w}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{4}} \:={x}^{\mathrm{4}} \:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{4}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:+{c}\:\:{but}\:{c}={w}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow{w}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}^{\mathrm{4}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${w}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\frac{{t}^{\mathrm{4}} −\mathrm{1}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\:\int_{\mathrm{0}} ^{{x}} \:\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{{x}} \:\:\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}\:\:+\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−{x}\:\:+{arctan}\left({x}\right)\:\Rightarrow \\ $$$${w}\left(\mathrm{1}\right)\:=−\frac{\mathrm{2}}{\mathrm{3}}\:+\frac{\pi}{\mathrm{4}}\:\:{generally}\:{let}\:{consider}\:{w}_{{p}} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+{p}}\:{x}^{\mathrm{2}{n}+{p}} \\ $$$${we}\:{have}\:{w}_{{p}} \left(\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+{p}\:}\:\:\:{and}\:{we}\:{have} \\ $$$${w}_{{p}} ^{'} \left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}+{p}−\mathrm{1}} \:\:=\:{x}^{{p}−\mathrm{1}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}_{{p}} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:+{c}\:{but}\:{c}={w}_{{p}} \left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{w}_{{p}} \left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$....{be}\:{continued}... \\ $$$$ \\ $$

Answered by rahul 19 last updated on 10/Aug/18

Commented by rahul 19 last updated on 10/Aug/18

≠ 0 ����

Commented by alex041103 last updated on 10/Aug/18

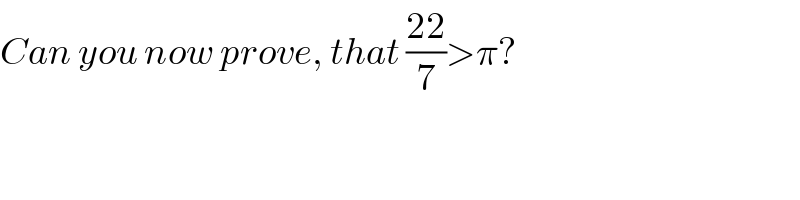
Can you now prove, that ((22)/7)>π?

$${Can}\:{you}\:{now}\:{prove},\:{that}\:\frac{\mathrm{22}}{\mathrm{7}}>\pi? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18

bah darun excellent...

$${bah}\:{darun}\:{excellent}... \\ $$

Commented by rahul 19 last updated on 10/Aug/18

Since integrand is non−negative & continous everywhere, it must be strictly positive in [0,1]. 0< ((22)/7)−π ⇒ ((22)/7)>π.

$$\mathrm{Since}\:\mathrm{integrand}\:\mathrm{is}\:\mathrm{non}−\mathrm{negative}\:\& \\ $$$$\mathrm{continous}\:\mathrm{everywhere},\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{strictly} \\ $$$$\mathrm{positive}\:\mathrm{in}\:\left[\mathrm{0},\mathrm{1}\right]. \\ $$$$\mathrm{0}<\:\frac{\mathrm{22}}{\mathrm{7}}−\pi\: \\ $$$$\Rightarrow\:\frac{\mathrm{22}}{\mathrm{7}}>\pi. \\ $$

Commented by alex041103 last updated on 10/Aug/18

Exactly. Also you can see thatfor 0<x<1 the integrand is small... this implies that ((22)/7) is good rational approximation for π.

$${Exactly}. \\ $$$${Also}\:{you}\:{can}\:{see}\:{thatfor}\:\mathrm{0}<{x}<\mathrm{1}\:{the} \\ $$$${integrand}\:{is}\:{small}...\:{this}\:{implies}\:{that} \\ $$$$\frac{\mathrm{22}}{\mathrm{7}}\:{is}\:\:{good}\:{rational}\:{approximation} \\ $$$${for}\:\pi. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com