
Question and Answers Forum
Question Number 41675 by Raj Singh last updated on 11/Aug/18

Commented by math khazana by abdo last updated on 12/Aug/18
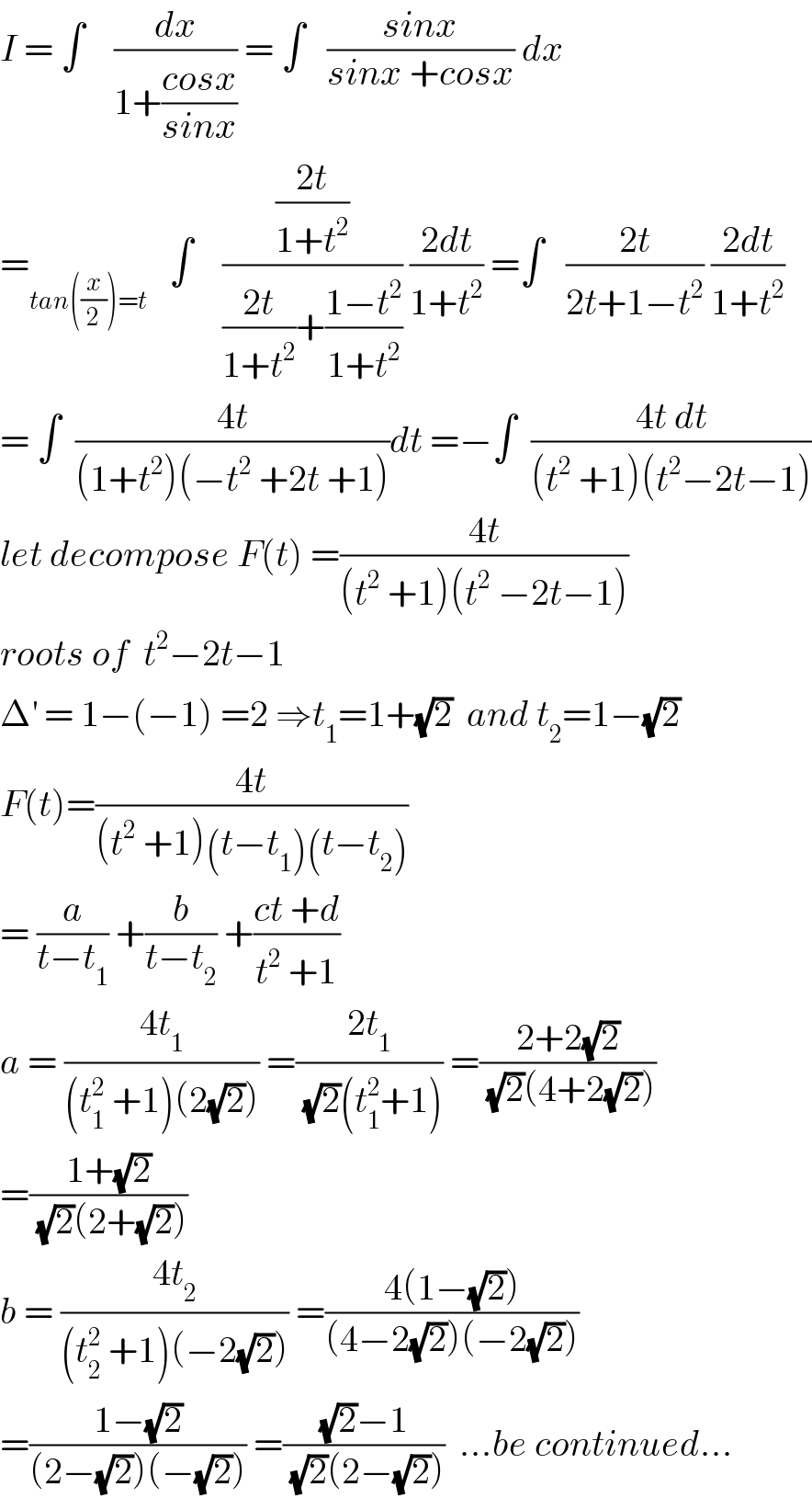
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18
![∫(dx/(1+cotx)) ∫((sinx)/(sinx+cosx))dx =(1/2)∫((cosx+sinx−(cosx−sinx))/(sinx+cosx))dx =(1/2)[∫dx−∫((cosx−sinx)/(sinx+cosx))dx =(1/2)[∫dx−∫((d(sinx+cosx))/(sinx+cosx))] =(1/2)[x−ln(sinx+cosx)]+c](Q41676.png)
| ||
Question and Answers Forum | ||
Question Number 41675 by Raj Singh last updated on 11/Aug/18 | ||
 | ||
Commented by math khazana by abdo last updated on 12/Aug/18 | ||
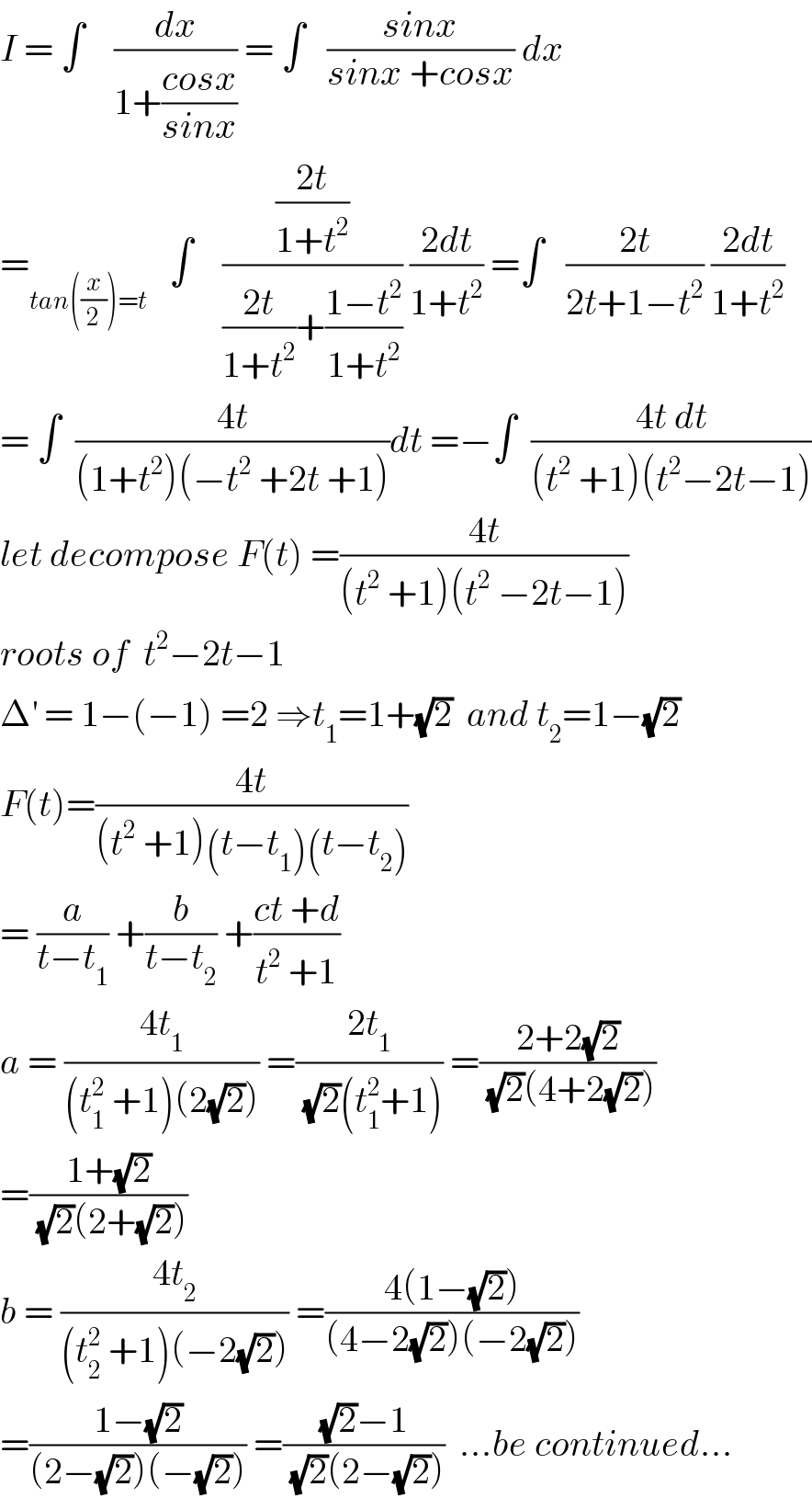 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18 | ||
![∫(dx/(1+cotx)) ∫((sinx)/(sinx+cosx))dx =(1/2)∫((cosx+sinx−(cosx−sinx))/(sinx+cosx))dx =(1/2)[∫dx−∫((cosx−sinx)/(sinx+cosx))dx =(1/2)[∫dx−∫((d(sinx+cosx))/(sinx+cosx))] =(1/2)[x−ln(sinx+cosx)]+c](Q41676.png) | ||
| ||