find radius of curvature to y=sin x at x=π/6 .


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 41682 by ajfour last updated on 11/Aug/18

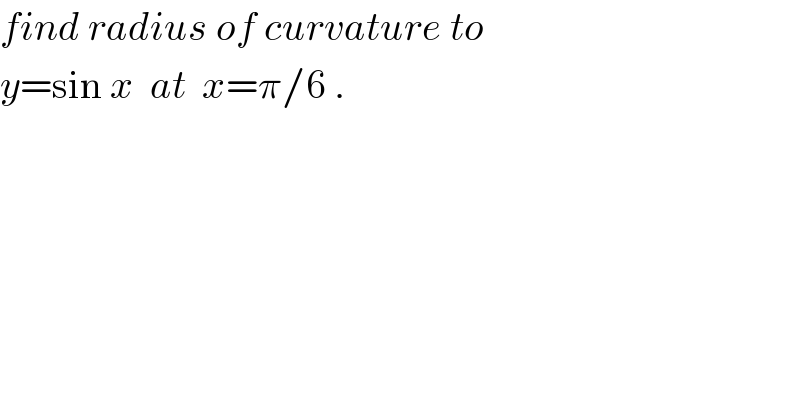
$f i n d r a d i u s o f c u r v a t u r e t o$ $y = \sin x a t x = π / 6 .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18
	$ds=rdθ ds=(√((dy)^2 +(dx)^2 )) (ds/dx)=(√(1+((dy/dx))^2 )) tanθ=(dy/dx) θ=tan^(−1) ((dy/dx)) (dθ/dx)=((d^2 y/dx^2 )/(1+((dy/dx))^2 )) r=(ds/dθ)=((ds/dx)/(dθ/dx))=∣(({1+((dy/dx))^2 }^(3/2) )/(d^2 y/dx^2 ))∣ y=sinx (dy/dx)=cosx so ((dy/dx))_(x=(Π/6)) =((√3)/2) (d^2 y/dx^2 )=−sinx so ((d^2 y/dx^2 ))_(x=(Π/6)) =−(1/2) r=∣(({1+(3/4)}^(3/2) )/(−(1/2)))∣.=2.((7/4))^(3/2)$
	$d s = r d θ$ $d s = \sqrt{{(d y)}^{2} + {(d x)}^{2}}$ $\frac{d s}{d x} = \sqrt{1 + {(\frac{d y}{d x})}^{2}}$ $t a n θ = \frac{d y}{d x}$ $θ = {t a n}^{- 1} (\frac{d y}{d x})$ $\frac{d θ}{d x} = \frac{\frac{d^{2} y}{{d x}^{2}}}{1 + {(\frac{d y}{d x})}^{2}}$ $r = \frac{d s}{d θ} = \frac{\frac{d s}{d x}}{\frac{d θ}{d x}} =∣ \frac{{1 + {(\frac{d y}{d x})}^{2}}^{\frac{3}{2}}}{\frac{d^{2} y}{{d x}^{2}}} ∣$ $y = s i n x$ $\frac{d y}{d x} = c o s x s o {(\frac{d y}{d x})}_{x = \frac{Π}{6}} = \frac{\sqrt{3}}{2}$ $\frac{d^{2} y}{{d x}^{2}} = - s i n x s o {(\frac{d^{2} y}{{d x}^{2}})}_{x = \frac{Π}{6}} = - \frac{1}{2}$ $r =∣ \frac{{1 + \frac{3}{4}}^{\frac{3}{2}}}{- \frac{1}{2}} ∣ . = 2 . {(\frac{7}{4})}^{\frac{3}{2}}$
	Commented by ajfour last updated on 11/Aug/18

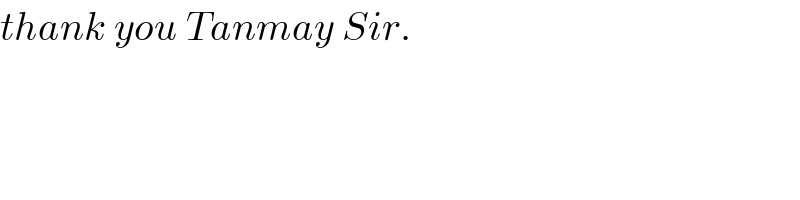
	$t h a n k y o u T a n m a y S i r .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18

	$t h a n k y o u a l s o f o r p o s t i n g v a r i e t y o f p r o b l e m$ $o f d i f f e r e n t t a s t e . . .$
	Answered by ajfour last updated on 11/Aug/18

	${[x - (\frac{π}{6} + r \sin θ)]}^{2} + {[y - (\frac{1}{2} + r \cos θ)]}^{2} = r^{2}$ $2 [x - (\frac{π}{6} + r \sin θ)] + 2 [y - (\frac{1}{2} + r \cos θ)] \frac{d y}{d x} = 0$ $1 + {(\frac{d y}{d x})}^{2} + [y - \frac{1}{2} - r \cos θ] \frac{d^{2} y}{{d x}^{2}} = 0$ $. . . . . . (i)$ $a n d \frac{d^{2} (\sin x)}{{d x}^{2}} ∣_{x = \frac{π}{6}} = - \frac{1}{2}$ $\frac{d y}{d x} ∣_{x = \frac{π}{6}} = \frac{\sqrt{3}}{2} = \tan θ$ $u s i n g t h e s e i n (i)$ $\Rightarrow 1 + \frac{3}{4} + (\frac{1}{2} - \frac{1}{2} - \frac{2 r}{\sqrt{7}}) (- \frac{1}{2}) = 0$ $\Rightarrow ∣ r ∣ = \frac{7 \sqrt{7}}{4} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum