
Question and Answers Forum
Question Number 41703 by abdo.msup.com last updated on 11/Aug/18
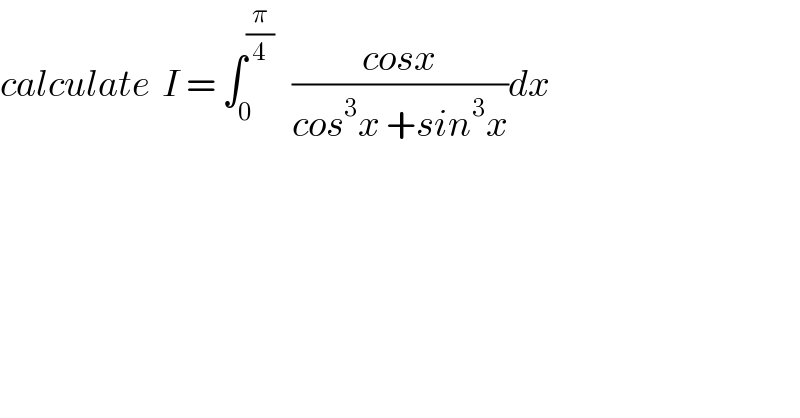
Commented by math khazana by abdo last updated on 12/Aug/18
![I = ∫_0 ^(π/4) (((cosx)/(cos^3 x))/((cos^3 x +sin^3 x)/(cos^3 x))) dx =∫_0 ^(π/4) (1/(cos^2 x(1+tan^3 x)))dx =∫_0 ^(π/4) ((1+tan^2 x)/(1+tan^3 x)) dx =_(tanx=t) ∫_0 ^1 ((1+t^2 )/(1+t^3 )) (dt/(1+t^2 )) = ∫_0 ^1 (dt/(1+t^3 )) let decompose F(t)= (1/(t^3 +1)) =(1/((t+1)(t^2 −t +1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t) =(1/3) lim_(t→+∞) tF(t)=0=a +b ⇒b=−(1/3) ⇒ F(t) = (1/(3(t+1))) +((−(1/3)t +c)/(t^2 −t +1)) F(0) =1 =(1/3) +c ⇒c=(2/3) ⇒ F(t) = (1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t +1)) ⇒ ∫_0 ^1 F(t)dt =(1/3)[ln∣t+1∣]_0 ^1 −(1/3) ∫_0 ^1 ((t−2)/(t^2 −t +1))dt =((ln(2))/3) −(1/6) ∫_0 ^1 ((2t−1−3)/(t^2 −t +1)) dt =((ln(2))/3) −[(1/6)ln∣t^2 −t+1∣ ]_0 ^1 +(1/2) ∫_0 ^1 (dt/(t^2 −t +1)) =((ln(2))/3) +(1/2) ∫_0 ^1 (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) ((ln(2))/3) +(1/2) (4/3) ∫_(−(1/(√3))) ^(1/(√3)) (1/(1+u^2 )) ((√3)/2) du =((ln(2))/3) + ((√3)/3) [ arctanu]_(−(1/(√3))) ^(1/(√3)) =((ln(2))/3) + (1/(√3)){ 2 arctan((1/(√3)))} =((ln(2))/3) +(2/(√3)) (π/6) ⇒ I = ((ln(2))/3) +(π/(3(√3))) .](Q41758.png)
| ||
Question and Answers Forum | ||
Question Number 41703 by abdo.msup.com last updated on 11/Aug/18 | ||
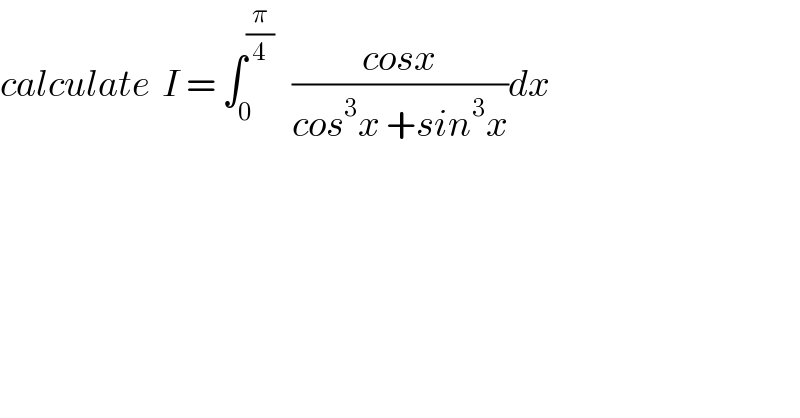 | ||
Commented by math khazana by abdo last updated on 12/Aug/18 | ||
![I = ∫_0 ^(π/4) (((cosx)/(cos^3 x))/((cos^3 x +sin^3 x)/(cos^3 x))) dx =∫_0 ^(π/4) (1/(cos^2 x(1+tan^3 x)))dx =∫_0 ^(π/4) ((1+tan^2 x)/(1+tan^3 x)) dx =_(tanx=t) ∫_0 ^1 ((1+t^2 )/(1+t^3 )) (dt/(1+t^2 )) = ∫_0 ^1 (dt/(1+t^3 )) let decompose F(t)= (1/(t^3 +1)) =(1/((t+1)(t^2 −t +1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t) =(1/3) lim_(t→+∞) tF(t)=0=a +b ⇒b=−(1/3) ⇒ F(t) = (1/(3(t+1))) +((−(1/3)t +c)/(t^2 −t +1)) F(0) =1 =(1/3) +c ⇒c=(2/3) ⇒ F(t) = (1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t +1)) ⇒ ∫_0 ^1 F(t)dt =(1/3)[ln∣t+1∣]_0 ^1 −(1/3) ∫_0 ^1 ((t−2)/(t^2 −t +1))dt =((ln(2))/3) −(1/6) ∫_0 ^1 ((2t−1−3)/(t^2 −t +1)) dt =((ln(2))/3) −[(1/6)ln∣t^2 −t+1∣ ]_0 ^1 +(1/2) ∫_0 ^1 (dt/(t^2 −t +1)) =((ln(2))/3) +(1/2) ∫_0 ^1 (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) ((ln(2))/3) +(1/2) (4/3) ∫_(−(1/(√3))) ^(1/(√3)) (1/(1+u^2 )) ((√3)/2) du =((ln(2))/3) + ((√3)/3) [ arctanu]_(−(1/(√3))) ^(1/(√3)) =((ln(2))/3) + (1/(√3)){ 2 arctan((1/(√3)))} =((ln(2))/3) +(2/(√3)) (π/6) ⇒ I = ((ln(2))/3) +(π/(3(√3))) .](Q41758.png) | ||