Previous in Relation and Functions Next in Relation and Functions
Question Number 41706 by abdo.msup.com last updated on 11/Aug/18
$${study}\:{the}\:{convergence}\:{of}\: \\ $$$${u}_{{n}} =\sum_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\mathrm{1}}{{kln}\left({k}\right)}\:−{ln}\left({ln}\left({n}\right)\right. \\ $$
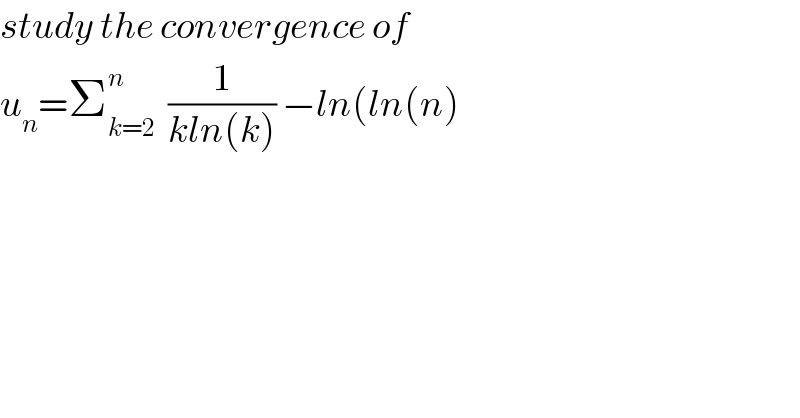
Commented by math khazana by abdo last updated on 13/Aug/18
![the function f(x) =(1/(xln(x))) is decreasing on [2,+∞[ so ∫_k ^(k+1) f(x)dx≤ f(k)≤ ∫_(k−1) ^k f(x)dx⇒ ∫_k ^(k+1) (dx/(xln(x))) ≤ f(k)≤ ∫_(k−1) ^k f(x)dx but ∫_k ^(k+1) (dx/(xln(x))) =[ln(lnx)]_k ^(k+1) =ln(ln(k+1))−ln(ln(k)) ⇒ Σ_(k=3) ^n ∫_k ^(k+1) (dx/(xln(x)))=Σ_(k=3) ^n {ln(ln(k+1))−ln(ln(k))} =ln(ln(n+1))−ln(ln(3)) also Σ_(k=3) ^n ∫_(k−1) ^k (dx/(xln(x))) =∫_2 ^n (dx/(xln(x))) =[ln(ln(x))]_2 ^n ln(ln(n))−ln(ln(2)) ⇒ ln(ln(n+1))−ln(ln(3))≤ Σ_(k=3) ^n f(k) ≤ ln(ln(n))−ln(ln(2))⇒ ln(ln(n+1))−ln(ln(3)) +(1/(2ln(2))) −lnln(n)≤ u_n ≤−ln(ln(2)) +(1/(2ln(2))) ⇒ ln(((ln(n+1))/(ln(n))))−ln(ln(3))+(1/(2ln(2))) ≤ u_n ≤(1/(2ln(2)))−ln(ln(2)) so u_n is convergente and (1/(2ln(2))) −ln(ln(3))≤ lim_(n→+∞) u_n ≤ (1/(2ln(2))) −ln(ln2)](Q41800.png)
$${the}\:{function}\:{f}\left({x}\right)\:=\frac{\mathrm{1}}{{xln}\left({x}\right)}\:{is}\:{decreasing}\:{on} \\ $$$$\left[\mathrm{2},+\infty\left[\:\:{so}\:\:\:\:\:\:\int_{{k}} ^{{k}+\mathrm{1}} {f}\left({x}\right){dx}\leqslant\:{f}\left({k}\right)\leqslant\:\int_{{k}−\mathrm{1}} ^{{k}} {f}\left({x}\right){dx}\Rightarrow\right.\right. \\ $$$$\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{dx}}{{xln}\left({x}\right)}\:\leqslant\:{f}\left({k}\right)\leqslant\:\int_{{k}−\mathrm{1}} ^{{k}} \:{f}\left({x}\right){dx}\:\:{but} \\ $$$$\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{{dx}}{{xln}\left({x}\right)}\:=\left[{ln}\left({lnx}\right)\right]_{{k}} ^{{k}+\mathrm{1}} ={ln}\left({ln}\left({k}+\mathrm{1}\right)\right)−{ln}\left({ln}\left({k}\right)\right) \\ $$$$\Rightarrow\:\sum_{{k}=\mathrm{3}} ^{{n}} \:\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{{dx}}{{xln}\left({x}\right)}=\sum_{{k}=\mathrm{3}} ^{{n}} \left\{{ln}\left({ln}\left({k}+\mathrm{1}\right)\right)−{ln}\left({ln}\left({k}\right)\right)\right\} \\ $$$$={ln}\left({ln}\left({n}+\mathrm{1}\right)\right)−{ln}\left({ln}\left(\mathrm{3}\right)\right)\:{also} \\ $$$$\sum_{{k}=\mathrm{3}} ^{{n}} \:\int_{{k}−\mathrm{1}} ^{{k}} \:\frac{{dx}}{{xln}\left({x}\right)}\:=\int_{\mathrm{2}} ^{{n}} \:\:\:\frac{{dx}}{{xln}\left({x}\right)}\:=\left[{ln}\left({ln}\left({x}\right)\right)\right]_{\mathrm{2}} ^{{n}} \\ $$$${ln}\left({ln}\left({n}\right)\right)−{ln}\left({ln}\left(\mathrm{2}\right)\right)\:\Rightarrow \\ $$$${ln}\left({ln}\left({n}+\mathrm{1}\right)\right)−{ln}\left({ln}\left(\mathrm{3}\right)\right)\leqslant\:\sum_{{k}=\mathrm{3}} ^{{n}} \:{f}\left({k}\right) \\ $$$$\leqslant\:\:{ln}\left({ln}\left({n}\right)\right)−{ln}\left({ln}\left(\mathrm{2}\right)\right)\Rightarrow\: \\ $$$${ln}\left({ln}\left({n}+\mathrm{1}\right)\right)−{ln}\left({ln}\left(\mathrm{3}\right)\right)\:+\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:−{lnln}\left({n}\right)\leqslant \\ $$$${u}_{{n}} \leqslant−{ln}\left({ln}\left(\mathrm{2}\right)\right)\:+\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:\Rightarrow \\ $$$${ln}\left(\frac{{ln}\left({n}+\mathrm{1}\right)}{{ln}\left({n}\right)}\right)−{ln}\left({ln}\left(\mathrm{3}\right)\right)+\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:\leqslant\:{u}_{{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}−{ln}\left({ln}\left(\mathrm{2}\right)\right) \\ $$$${so}\:{u}_{{n}} \:{is}\:{convergente}\:{and}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:−{ln}\left({ln}\left(\mathrm{3}\right)\right)\leqslant\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} \leqslant\:\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:−{ln}\left({ln}\mathrm{2}\right) \\ $$
Answered by alex041103 last updated on 12/Aug/18
![We clearly see that (d/dk)((1/(kln(k))))<0 We apply the integral test: u_∞ ≈lim_(n→∞) [∫_2 ^n (dk/(kln(k))) − ln(ln(n))]= =lim_(n→∞) [∫_2 ^n ((d(ln(k)))/(ln(k))) − ln(ln(n))]= =lim_(n→∞) [ln(ln(n))−ln(ln(2))−ln(ln(n))] =−ln(ln(2)) As we know ln≡log_e and e≈2.718 ⇒Since 1<2<e 0<ln(2)<1 Since ln(2)>0 then ln(ln(2)) exists. ⇒u_n converges](Q41759.png)
$${We}\:{clearly}\:{see}\:{that}\:\frac{{d}}{{dk}}\left(\frac{\mathrm{1}}{{kln}\left({k}\right)}\right)<\mathrm{0} \\ $$$${We}\:{apply}\:{the}\:{integral}\:{test}: \\ $$$${u}_{\infty} \approx\underset{{n}\rightarrow\infty} {{lim}}\left[\int_{\mathrm{2}} ^{{n}} \frac{{dk}}{{kln}\left({k}\right)}\:−\:{ln}\left({ln}\left({n}\right)\right)\right]= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left[\int_{\mathrm{2}} ^{{n}} \frac{{d}\left({ln}\left({k}\right)\right)}{{ln}\left({k}\right)}\:−\:{ln}\left({ln}\left({n}\right)\right)\right]= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left({ln}\left({n}\right)\right)−{ln}\left({ln}\left(\mathrm{2}\right)\right)−{ln}\left({ln}\left({n}\right)\right)\right] \\ $$$$=−{ln}\left({ln}\left(\mathrm{2}\right)\right) \\ $$$${As}\:{we}\:{know}\:{ln}\equiv{log}_{{e}} \:{and}\:{e}\approx\mathrm{2}.\mathrm{718} \\ $$$$\Rightarrow{Since}\:\mathrm{1}<\mathrm{2}<{e}\:\mathrm{0}<{ln}\left(\mathrm{2}\right)<\mathrm{1} \\ $$$${Since}\:{ln}\left(\mathrm{2}\right)>\mathrm{0}\:{then}\:{ln}\left({ln}\left(\mathrm{2}\right)\right)\:{exists}. \\ $$$$\Rightarrow{u}_{{n}} \:{converges} \\ $$