Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 41806 by Raj Singh last updated on 13/Aug/18

Commented by prof Abdo imad last updated on 13/Aug/18

let A = ∫ ((arcsin(.(√x))−arccos((√x)))/(arcsin(√x) +arccos(√x))) dx arcosx +arcsinx)^′ =−(1/(√(1−x^2 ))) +(1/(√(1−x^2 ))) for −1<x<1 ⇒arcoss+arcsinx =c c=(π/2) ⇒A = ∫ ((arcsin(√x)−((π/2)−arcsin(√x)))/(arcsin(√x)+(π/2) −arcsin(√x)))dx =(2/π) ∫ (2arcsin(√x) −(π/2))dx =(4/π) ∫ arcsin((√x))dx −x +c but ∫ arcsin((√x))dx =_((√x)=t) ∫ 2 arcsin(t)t dt =2 ∫ t arcsin(t)dt (by parts) =2{ (t^2 /2) arcsint −∫ (t^2 /(2(√(1−t^2 ))))dt} =t^2 arcsint − ∫ (t^2 /(√(1−t^2 ))) dt but ∫ (t^2 /(√(1−t^2 ))) dt =_(t=sinκ) ∫ ((sin^2 α)/(cosα)) cosα dα =∫ ((1−cos(2α))/2) dα =(1/2) α −(1/4)sin(2α) =(1/2)α −(1/2) cosαsinα =(1/2) arcsint−(1/2)t(√(1−t^2 )) =(1/2) arcsin((√x))−(1/2)(√x)(√(1−x)) ⇒ A =(4/π){x arcsin((√x))−(1/2)arcsin((√x))+(1/2)(√x)(√(1−x))}−x +c A =(4/π){(x−(1/2))arcsin((√x)) +(((√x)(√(1−x)))/2)}−x +c .

$${let}\:{A}\:=\:\int\:\:\frac{{arcsin}\left(.\sqrt{{x}}\right)−{arccos}\left(\sqrt{{x}}\right)}{{arcsin}\sqrt{{x}}\:+{arccos}\sqrt{{x}}}\:{dx} \\ $$$$\left.{arcosx}\:+{arcsinx}\right)^{'} =−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{for} \\ $$$$−\mathrm{1}<{x}<\mathrm{1}\:\Rightarrow{arcoss}+{arcsinx}\:={c} \\ $$$${c}=\frac{\pi}{\mathrm{2}}\:\Rightarrow{A}\:=\:\int\:\frac{{arcsin}\sqrt{{x}}−\left(\frac{\pi}{\mathrm{2}}−{arcsin}\sqrt{{x}}\right)}{{arcsin}\sqrt{{x}}+\frac{\pi}{\mathrm{2}}\:−{arcsin}\sqrt{{x}}}{dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\:\int\:\:\left(\mathrm{2}{arcsin}\sqrt{{x}}\:−\frac{\pi}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{4}}{\pi}\:\int\:\:{arcsin}\left(\sqrt{{x}}\right){dx}\:−{x}\:+{c}\:\:\:{but} \\ $$$$\int\:\:\:{arcsin}\left(\sqrt{{x}}\right){dx}\:=_{\sqrt{{x}}={t}} \:\:\:\int\:\:\mathrm{2}\:{arcsin}\left({t}\right){t}\:{dt} \\ $$$$=\mathrm{2}\:\int\:\:{t}\:{arcsin}\left({t}\right){dt}\:\:\:\left({by}\:{parts}\right) \\ $$$$=\mathrm{2}\left\{\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:{arcsint}\:\:−\int\:\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}\right\} \\ $$$$={t}^{\mathrm{2}} \:{arcsint}\:−\:\int\:\:\frac{{t}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:{dt}\:{but} \\ $$$$\int\:\:\:\frac{{t}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:{dt}\:=_{{t}={sin}\kappa} \:\:\:\:\int\:\:\:\:\frac{{sin}^{\mathrm{2}} \alpha}{{cos}\alpha}\:{cos}\alpha\:{d}\alpha \\ $$$$=\int\:\:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}\:{d}\alpha\:=\frac{\mathrm{1}}{\mathrm{2}}\:\alpha\:−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\alpha\:−\frac{\mathrm{1}}{\mathrm{2}}\:{cos}\alpha{sin}\alpha\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arcsint}−\frac{\mathrm{1}}{\mathrm{2}}{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{arcsin}\left(\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}\:\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{4}}{\pi}\left\{{x}\:{arcsin}\left(\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}\right\}−{x}\:+{c} \\ $$$${A}\:=\frac{\mathrm{4}}{\pi}\left\{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right){arcsin}\left(\sqrt{{x}}\right)\:+\frac{\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}{\mathrm{2}}\right\}−{x}\:+{c}\:. \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Aug/18

x=sin^2 ∝ dx=2sin∝cos∝d∝ sin^(−1) (sin∝)+cos^(−1) (sin∝) sin^(−1) (sin∝)+cos^(−1) {cos((Π/2)−∝)} =(Π/2) sin^(−1) (sin∝)−cos^(−1) (sin∝) =2∝−(Π/2) ∫(((2∝−(Π/2))sin2∝.d∝)/(Π/2)) (2/Π)[∫2∝sin2∝d∝−(Π/2)∫sin2∝ d∝] (4/Π)∫∝sin2∝d∝−∫sin2∝d∝ (4/Π)[∝.(((−cos2∝)/2))−∫1.(((−cos2∝)/2))d∝]+((cos2∝)/2)+c (4/Π)[∝.(((−cos2∝)/2))+((sin2∝)/4)]+((cos2∝)/2)+cc cos2∝.(((−2∝)/Π)+(1/2))+sin2∝.(1/Π)+c (((Π−4∝)/(2Π)))cos2∝+(1/Π)sin2∝+c (((Π−4∝)/(2Π)))(cos^2 ∝−sin^2 ∝)+(1/Π)(2sin∝cos∝)+c (((Π−4∝)/(2Π)))(1−x−x)+(1/Π)(2.(√x) .(√(1−x)) )+c (((Π−4sin^(−1) (√x))/(2Π)))(1−2x)+(1/Π)(2(√x) .(√(1−x)) )+c pls check

$${x}={sin}^{\mathrm{2}} \propto\:\:{dx}=\mathrm{2}{sin}\propto{cos}\propto{d}\propto \\ $$$${sin}^{−\mathrm{1}} \left({sin}\propto\right)+{cos}^{−\mathrm{1}} \left({sin}\propto\right) \\ $$$${sin}^{−\mathrm{1}} \left({sin}\propto\right)+{cos}^{−\mathrm{1}} \left\{{cos}\left(\frac{\Pi}{\mathrm{2}}−\propto\right)\right\} \\ $$$$=\frac{\Pi}{\mathrm{2}} \\ $$$${sin}^{−\mathrm{1}} \left({sin}\propto\right)−{cos}^{−\mathrm{1}} \left({sin}\propto\right) \\ $$$$=\mathrm{2}\propto−\frac{\Pi}{\mathrm{2}} \\ $$$$\int\frac{\left(\mathrm{2}\propto−\frac{\Pi}{\mathrm{2}}\right){sin}\mathrm{2}\propto.{d}\propto}{\frac{\Pi}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}}{\Pi}\left[\int\mathrm{2}\propto{sin}\mathrm{2}\propto{d}\propto−\frac{\Pi}{\mathrm{2}}\int{sin}\mathrm{2}\propto\:{d}\propto\right] \\ $$$$\frac{\mathrm{4}}{\Pi}\int\propto{sin}\mathrm{2}\propto{d}\propto−\int{sin}\mathrm{2}\propto{d}\propto \\ $$$$\frac{\mathrm{4}}{\Pi}\left[\propto.\left(\frac{−{cos}\mathrm{2}\propto}{\mathrm{2}}\right)−\int\mathrm{1}.\left(\frac{−{cos}\mathrm{2}\propto}{\mathrm{2}}\right){d}\propto\right]+\frac{{cos}\mathrm{2}\propto}{\mathrm{2}}+{c} \\ $$$$\frac{\mathrm{4}}{\Pi}\left[\propto.\left(\frac{−{cos}\mathrm{2}\propto}{\mathrm{2}}\right)+\frac{{sin}\mathrm{2}\propto}{\mathrm{4}}\right]+\frac{{cos}\mathrm{2}\propto}{\mathrm{2}}+{cc} \\ $$$${cos}\mathrm{2}\propto.\left(\frac{−\mathrm{2}\propto}{\Pi}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{sin}\mathrm{2}\propto.\frac{\mathrm{1}}{\Pi}+{c} \\ $$$$\left(\frac{\Pi−\mathrm{4}\propto}{\mathrm{2}\Pi}\right){cos}\mathrm{2}\propto+\frac{\mathrm{1}}{\Pi}{sin}\mathrm{2}\propto+{c} \\ $$$$\left(\frac{\Pi−\mathrm{4}\propto}{\mathrm{2}\Pi}\right)\left({cos}^{\mathrm{2}} \propto−{sin}^{\mathrm{2}} \propto\right)+\frac{\mathrm{1}}{\Pi}\left(\mathrm{2}{sin}\propto{cos}\propto\right)+{c} \\ $$$$\left(\frac{\Pi−\mathrm{4}\propto}{\mathrm{2}\Pi}\right)\left(\mathrm{1}−{x}−{x}\right)+\frac{\mathrm{1}}{\Pi}\left(\mathrm{2}.\sqrt{{x}}\:.\sqrt{\mathrm{1}−{x}}\:\right)+{c} \\ $$$$\left(\frac{\Pi−\mathrm{4}{sin}^{−\mathrm{1}} \sqrt{{x}}}{\mathrm{2}\Pi}\right)\left(\mathrm{1}−\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\Pi}\left(\mathrm{2}\sqrt{{x}}\:.\sqrt{\mathrm{1}−{x}}\:\right)+{c}\:\:{pls}\:{check} \\ $$$$ \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 13/Aug/18

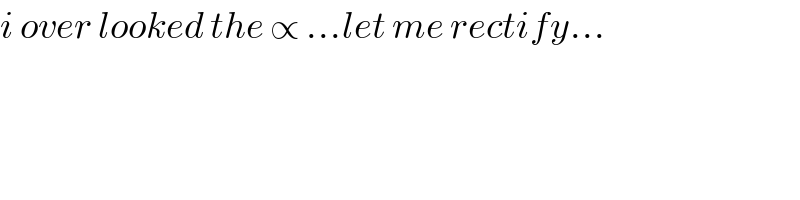
i over looked the ∝ ...let me rectify...

$${i}\:{over}\:{looked}\:{the}\:\propto\:...{let}\:{me}\:{rectify}... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 13/Aug/18

rectified by red colour...

$${rectified}\:{by}\:{red}\:{colour}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com