let f(a) = ∫_0 ^(π/2) (dx/(1+asinx)) with a∈R 1) find a simple form of f(a) 2) calculate ∫_0 ^(π/2) (dx/(1+sinx)) and ∫_0 ^(π/2) (dx/(1+2sinx)) 3) find the value of ∫_0 ^(π/2) ((cosx)/((1+asinx)^2 ))dx 4) find the value of ∫_0 ^(π/2) ((cosx)/((1+sinx)^2 ))dx and ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 41848 by maxmathsup by imad last updated on 13/Aug/18

$l e t f (a) = \int_{0}^{\frac{π}{2}} \frac{d x}{1 + a s i n x} w i t h a \in R$ $1) f i n d a s i m p l e f o r m o f f (a)$ $2) c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{d x}{1 + s i n x} a n d \int_{0}^{\frac{π}{2}} \frac{d x}{1 + 2 s i n x}$ $3) f i n d t h e v a l u e o f \int_{0}^{\frac{π}{2}} \frac{c o s x}{{(1 + a s i n x)}^{2}} d x$ $4) f i n d t h e v a l u e o f \int_{0}^{\frac{π}{2}} \frac{c o s x}{{(1 + s i n x)}^{2}} d x a n d \int_{0}^{\frac{π}{2}} \frac{c o s x}{{(1 + 2 s i n x)}^{2}} d x$
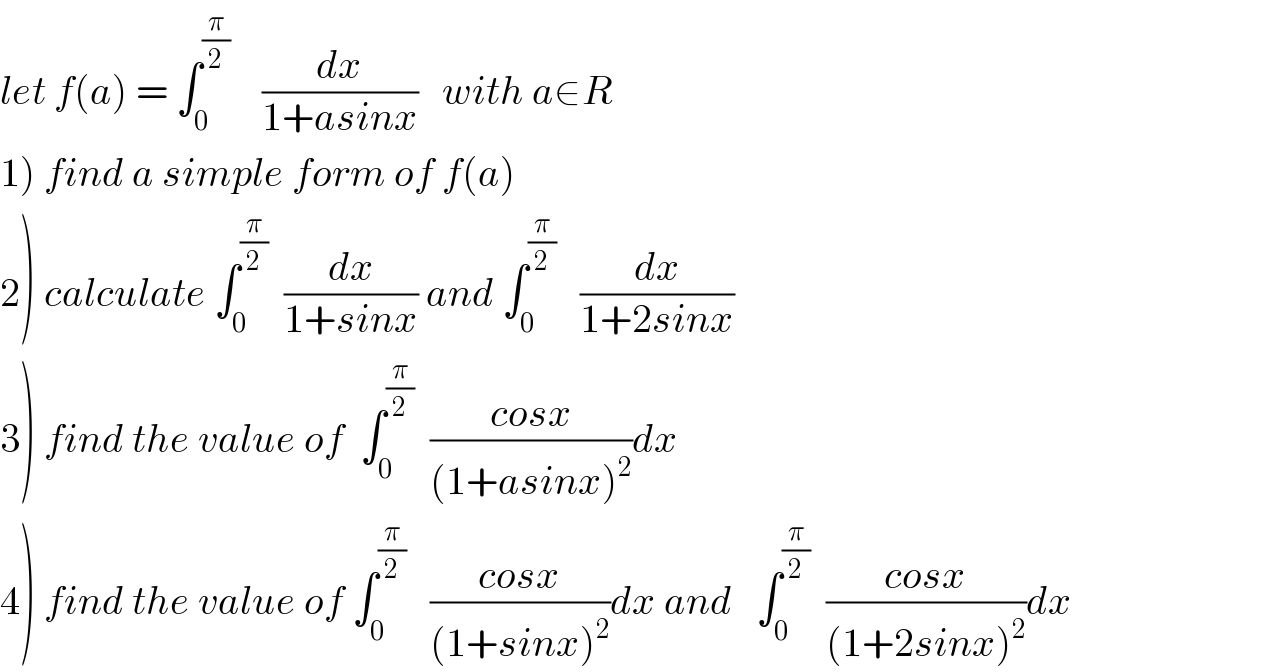
Commented by maxmathsup by imad last updated on 14/Aug/18
$1) changement tan((x/2))=t give f(a) = ∫_0 ^1 (1/(1+a((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^1 ((2dt)/(1+t^2 +2at)) =∫_0 ^1 ((2dt)/(t^2 +2at +1)) roots of t^2 +2at +1 Δ^′ =a^2 −1 case 1 a^2 >1 ⇒ ∣a∣>1 ⇒ t_1 =−a +(√(a^2 −1)) qnd t_2 =−a−(√(a^2 −1)) and F(t) =(2/(t^2 +2at +1)) =(2/((t−t_1 )(t−t_2 ))) =(α/(t−t_1 )) +(β/(t−t_2 )) α = (2/(t_1 −t_2 )) = (2/(2(√(a^2 −1)))) = (1/(√(a^2 −1))) and β =(2/(t_2 −t_1 )) =−(1/(√(a^2 −1))) ⇒ F(t) =(1/(√(a^2 −1))){ (1/(t−t_1 )) −(1/(t−t_2 ))} ⇒f(a) =∫_0 ^1 (1/(√(a^2 −1))){ (1/(t−t_1 ))−(1/(t−t_2 ))}dt = (1/(√(a^2 −1))) [ln∣ ((t−t_1 )/(t−t_2 ))∣]_0 ^1 = (1/(√(a^2 −1))) { ln∣ ((1+a−(√(a^2 −1)))/(1+a+(√(a^2 −1))))∣−ln∣ ((a−(√(a^2 −1)))/(a+(√(a^2 −1))))∣} case 2 a^2 <1 ⇒ −1<a<1 ⇒ no real roots ⇒ f(a) =∫_0 ^1 ((2dt)/(t^2 +2at +a^2 +1−a^2 )) = ∫_0 ^1 ((2dt)/((t+a)^2 +1−a^2 )) changement t+a =(√(1−a^2 ))u give f(a) = ∫_(a/(√(1−a^2 ))) ^((1+a)/(√(1−a^2 ))) ((2 (√(1−a^2 ))du)/((1−a^2 )(1+u^2 ))) = (2/(√(1−a^2 ))) { arctan(((1+a)/(√(1−a^2 ))))−arctan((a/(√(1−a^2 ))))}$
$1) c h a n g e m e n t t a n (\frac{x}{2}) = t g i v e$ $f (a) = \int_{0}^{1} \frac{1}{1 + a \frac{2 t}{1 + t^{2}}} \frac{2 d t}{1 + t^{2}} = \int_{0}^{1} \frac{2 d t}{1 + t^{2} + 2 a t} = \int_{0}^{1} \frac{2 d t}{t^{2} + 2 a t + 1}$ $r o o t s o f t^{2} + 2 a t + 1$ $Δ^{^{'}} = a^{2} - 1$ $c a s e 1 a^{2} > 1 \Rightarrow ∣ a ∣> 1 \Rightarrow t_{1} = - a + \sqrt{a^{2} - 1} q n d t_{2} = - a - \sqrt{a^{2} - 1} a n d$ $F (t) = \frac{2}{t^{2} + 2 a t + 1} = \frac{2}{(t - t_{1}) (t - t_{2})} = \frac{α}{t - t_{1}} + \frac{β}{t - t_{2}}$ $α = \frac{2}{t_{1} - t_{2}} = \frac{2}{2 \sqrt{a^{2} - 1}} = \frac{1}{\sqrt{a^{2} - 1}} a n d β = \frac{2}{t_{2} - t_{1}} = - \frac{1}{\sqrt{a^{2} - 1}} \Rightarrow$ $F (t) = \frac{1}{\sqrt{a^{2} - 1}} {\frac{1}{t - t_{1}} - \frac{1}{t - t_{2}}} \Rightarrow f (a) = \int_{0}^{1} \frac{1}{\sqrt{a^{2} - 1}} {\frac{1}{t - t_{1}} - \frac{1}{t - t_{2}}} d t$ $= \frac{1}{\sqrt{a^{2} - 1}} {[l n ∣ \frac{t - t_{1}}{t - t_{2}} ∣]}_{0}^{1} = \frac{1}{\sqrt{a^{2} - 1}} {l n ∣ \frac{1 + a - \sqrt{a^{2} - 1}}{1 + a + \sqrt{a^{2} - 1}} ∣ - l n ∣ \frac{a - \sqrt{a^{2} - 1}}{a + \sqrt{a^{2} - 1}} ∣}$ $c a s e 2 a^{2} < 1 \Rightarrow - 1 < a < 1 \Rightarrow n o r e a l r o o t s \Rightarrow$ $f (a) = \int_{0}^{1} \frac{2 d t}{t^{2} + 2 a t + a^{2} + 1 - a^{2}} = \int_{0}^{1} \frac{2 d t}{{(t + a)}^{2} + 1 - a^{2}} c h a n g e m e n t$ $t + a = \sqrt{1 - a^{2}} u g i v e f (a) = \int_{\frac{a}{\sqrt{1 - a^{2}}}}^{\frac{1 + a}{\sqrt{1 - a^{2}}}} \frac{2 \sqrt{1 - a^{2}} d u}{(1 - a^{2}) (1 + u^{2})}$ $= \frac{2}{\sqrt{1 - a^{2}}} {a r c t a n (\frac{1 + a}{\sqrt{1 - a^{2}}}) - a r c t a n (\frac{a}{\sqrt{1 - a^{2}}})}$
Commented by maxmathsup by imad last updated on 14/Aug/18
$2) ∫_0 ^(π/2) (dx/(1+2sinx)) =f(2) = (1/(√3)){ ln∣ ((3−(√3))/(3+(√3)))∣ −ln∣ ((2−(√3))/(2+(√3)))∣} =(1/(√3)){ ln(((3−(√3))/(3+(√3))))−ln(((2−(√3))/(2+(√3))))} let calculate ∫_0 ^(π/2) (dx/(1+sinx)) ∫_0 ^(π/2) (dx/(1+sinx)) =_(tan((x/2)) =u) ∫_0 ^1 (1/(1+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫_0 ^1 ((2du)/(1+u^2 +2t)) = ∫_0 ^1 ((2du)/((u+1)^2 )) =[((−2)/(1+u))]_0 ^1 =−2((1/2) −1)= 1 .$
$2) \int_{0}^{\frac{π}{2}} \frac{d x}{1 + 2 s i n x} = f (2) = \frac{1}{\sqrt{3}} {l n ∣ \frac{3 - \sqrt{3}}{3 + \sqrt{3}} ∣ - l n ∣ \frac{2 - \sqrt{3}}{2 + \sqrt{3}} ∣}$ $= \frac{1}{\sqrt{3}} {l n (\frac{3 - \sqrt{3}}{3 + \sqrt{3}}) - l n (\frac{2 - \sqrt{3}}{2 + \sqrt{3}})} l e t c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{d x}{1 + s i n x}$ $\int_{0}^{\frac{π}{2}} \frac{d x}{1 + s i n x} =_{t a n (\frac{x}{2}) = u} \int_{0}^{1} \frac{1}{1 + \frac{2 u}{1 + u^{2}}} \frac{2 d u}{1 + u^{2}} = \int_{0}^{1} \frac{2 d u}{1 + u^{2} + 2 t}$ $= \int_{0}^{1} \frac{2 d u}{{(u + 1)}^{2}} = {[\frac{- 2}{1 + u}]}_{0}^{1} = - 2 (\frac{1}{2} - 1) = 1 .$
Commented by maxmathsup by imad last updated on 15/Aug/18
$3) we have f(a) = ∫_0 ^(π/2) (dx/(1+a sinx)) ⇒f^′ (a) =−∫_0 ^(π/2) ((sinx)/((1+asinx)^2 )) dx ⇒ ∫_0 ^(π/2) ((sinx)/((1+a sinx)^2 )) dx =−f^′ (a) if −1<a<1 f(a) = (2/(√(1−a^2 ))){ arctan(((1+a)/(√(1−a^2 ))))−arctan((a/(√(1−a^2 )))) ⇒ f^′ (a) = 2 (−((−a)/(√(1−a^2 ))))×(1/((1−a^2 ))){ arctan(((1+a)/(√(1−a^2 ))))−arctan((a/(√(1−a^2 ))))} +(2/(√(1−a^2 ))) { (((((1+a)/(√(1−a^2 ))))^′ )/(1+(((1+a)/(√(1−a^2 ))))^2 )) −((((a/(√(1−a^2 ))))^′ )/(1+((a/(√(1−a^2 ))))^2 ))} but (((1+a)/(√(1−a^2 ))))^′ =(((√(1−a^2 )) −(1+a)(((−2a)/(2(√(1−a^2 ))))))/(1−a^2 )) = ((1−a^2 +a+a^2 )/((1−a^2 )(√(1−a^2 )))) =((1+a)/((1−a^2 )(√(1−a^2 )))) ((a/(√(1−a^2 ))))^′ = (((√(1−a^2 )) −a (((−a)/(√(1−a^2 )))))/((1−a^2 ))) =((1−a^2 +a^2 )/((1−a^2 )(√(1−a^2 )))) =(1/((1−a^2 )(√(1−a^2 )))) ⇒ f^′ (a) = ((2a)/((1−a^2 )(√(1−a^2 )))){ arctan(((1+a)/(√(1−a^2 )))) −arctan((a/(√(1−a^2 ))))} +(2/(√(1−a^2 ))){ ((1+a)/((1−a^2 )(√(1−a^2 ))(1+(((1+a)^2 )/(1−a^2 ))))) − (1/((1−a^2 )(√(1−a^2 ))(1+(a^2 /(1−a^2 )))))} if ∣a∣>1 we follow the same way .$
$3) w e h a v e f (a) = \int_{0}^{\frac{π}{2}} \frac{d x}{1 + a s i n x} \Rightarrow f^{^{'}} (a) = - \int_{0}^{\frac{π}{2}} \frac{s i n x}{{(1 + a s i n x)}^{2}} d x$ $\Rightarrow \int_{0}^{\frac{π}{2}} \frac{s i n x}{{(1 + a s i n x)}^{2}} d x = - f^{^{'}} (a)$ $i f - 1 < a < 1 f (a) = \frac{2}{\sqrt{1 - a^{2}}} {a r c t a n (\frac{1 + a}{\sqrt{1 - a^{2}}}) - a r c t a n (\frac{a}{\sqrt{1 - a^{2}}}) \Rightarrow$ $f^{^{'}} (a) = 2 (- \frac{- a}{\sqrt{1 - a^{2}}}) \times \frac{1}{(1 - a^{2})} {a r c t a n (\frac{1 + a}{\sqrt{1 - a^{2}}}) - a r c t a n (\frac{a}{\sqrt{1 - a^{2}}})}$ $+ \frac{2}{\sqrt{1 - a^{2}}} {\frac{{(\frac{1 + a}{\sqrt{1 - a^{2}}})}^{^{'}}}{1 + {(\frac{1 + a}{\sqrt{1 - a^{2}}})}^{2}} - \frac{{(\frac{a}{\sqrt{1 - a^{2}}})}^{^{'}}}{1 + {(\frac{a}{\sqrt{1 - a^{2}}})}^{2}}} b u t$ ${(\frac{1 + a}{\sqrt{1 - a^{2}}})}^{^{'}} = \frac{\sqrt{1 - a^{2}} - (1 + a) (\frac{- 2 a}{2 \sqrt{1 - a^{2}}})}{1 - a^{2}} = \frac{1 - a^{2} + a + a^{2}}{(1 - a^{2}) \sqrt{1 - a^{2}}} = \frac{1 + a}{(1 - a^{2}) \sqrt{1 - a^{2}}}$ ${(\frac{a}{\sqrt{1 - a^{2}}})}^{^{'}} = \frac{\sqrt{1 - a^{2}} - a (\frac{- a}{\sqrt{1 - a^{2}}})}{(1 - a^{2})} = \frac{1 - a^{2} + a^{2}}{(1 - a^{2}) \sqrt{1 - a^{2}}} = \frac{1}{(1 - a^{2}) \sqrt{1 - a^{2}}} \Rightarrow$ $f^{^{'}} (a) = \frac{2 a}{(1 - a^{2}) \sqrt{1 - a^{2}}} {a r c t a n (\frac{1 + a}{\sqrt{1 - a^{2}}}) - a r c t a n (\frac{a}{\sqrt{1 - a^{2}}})}$ $+ \frac{2}{\sqrt{1 - a^{2}}} {\frac{1 + a}{(1 - a^{2}) \sqrt{1 - a^{2}} (1 + \frac{{(1 + a)}^{2}}{1 - a^{2}})} - \frac{1}{(1 - a^{2}) \sqrt{1 - a^{2}} (1 + \frac{a^{2}}{1 - a^{2}})}}$ $i f ∣ a ∣> 1 w e f o l l o w t h e s a m e w a y .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum