Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 41911 by lucha116 last updated on 15/Aug/18

h(x)=(√(sin^4 x+cos^4 x−2msinxcosx)) Find all the values of the parameter m for the funtion denined on R

$${h}\left({x}\right)=\sqrt{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}−\mathrm{2}{msinxcosx}} \\ $$$${Find}\:{all}\:{the}\:{values}\:{of}\:{the}\:{parameter}\:{m}\:{for}\:{the}\:{funtion}\:{denined}\:{on}\:{R} \\ $$$$ \\ $$

Commented by MJS last updated on 15/Aug/18

draw the function for ∣m∣>(1/2), you will see that it′s not defined ∀x∈R m=1 ⇒ sin^4 (π/4) +cos^4 (π/4) −2sin (π/4) cos (π/4)= =(1/4)+(1/4)−2×((√2)/2)×((√2)/2)=−(1/2) as I hopefully showed the minimum of sin^4 x +cos^4 x −2msin x cos x must be ≥0 and it′s exactly zero for m=±(1/2). for ∣m∣>(1/2) the minimum is below zero

$$\mathrm{draw}\:\mathrm{the}\:\mathrm{function}\:\mathrm{for}\:\mid{m}\mid>\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{you}\:\mathrm{will}\:\mathrm{see} \\ $$$$\mathrm{that}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{defined}\:\forall{x}\in\mathbb{R} \\ $$$${m}=\mathrm{1}\:\Rightarrow\:\mathrm{sin}^{\mathrm{4}} \:\frac{\pi}{\mathrm{4}}\:+\mathrm{cos}^{\mathrm{4}} \:\frac{\pi}{\mathrm{4}}\:−\mathrm{2sin}\:\frac{\pi}{\mathrm{4}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{2}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{as}\:\mathrm{I}\:\mathrm{hopefully}\:\mathrm{showed}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}\:+\mathrm{cos}^{\mathrm{4}} \:{x}\:−\mathrm{2}{m}\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:\mathrm{must}\:\mathrm{be}\:\geqslant\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{zero}\:\mathrm{for}\:{m}=\pm\frac{\mathrm{1}}{\mathrm{2}}.\:\mathrm{for}\:\mid{m}\mid>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{below}\:\mathrm{zero} \\ $$

Commented by math khazana by abdo last updated on 15/Aug/18

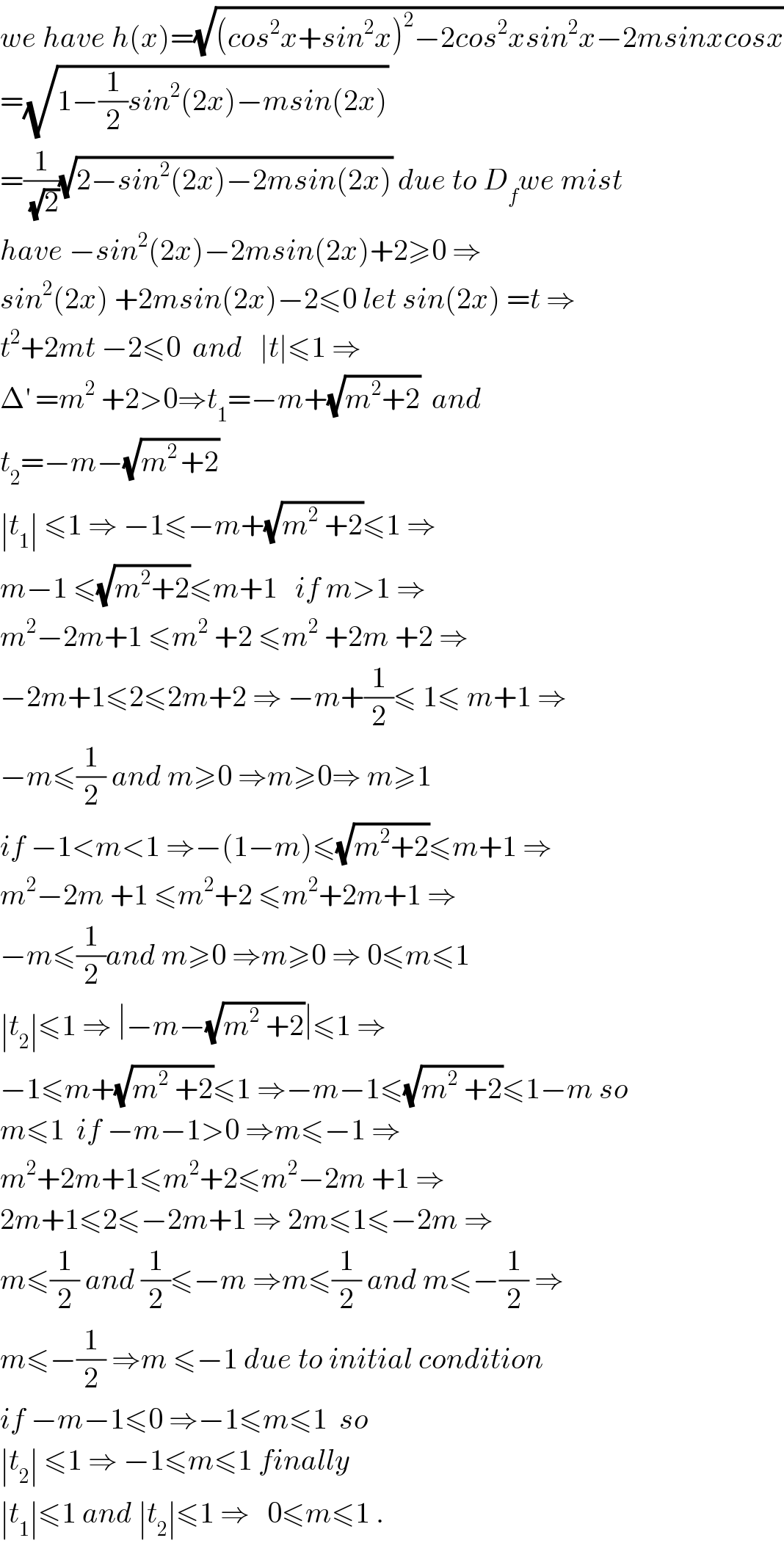
we have h(x)=(√((cos^2 x+sin^2 x)^2 −2cos^2 xsin^2 x−2msinxcosx)) =(√(1−(1/2)sin^2 (2x)−msin(2x))) =(1/(√2))(√(2−sin^2 (2x)−2msin(2x))) due to D_f we mist have −sin^2 (2x)−2msin(2x)+2≥0 ⇒ sin^2 (2x) +2msin(2x)−2≤0 let sin(2x) =t ⇒ t^2 +2mt −2≤0 and ∣t∣≤1 ⇒ Δ^′ =m^2 +2>0⇒t_1 =−m+(√(m^2 +2)) and t_2 =−m−(√(m^(2 ) +2)) ∣t_1 ∣ ≤1 ⇒ −1≤−m+(√(m^2 +2))≤1 ⇒ m−1 ≤(√(m^2 +2))≤m+1 if m>1 ⇒ m^2 −2m+1 ≤m^2 +2 ≤m^2 +2m +2 ⇒ −2m+1≤2≤2m+2 ⇒ −m+(1/2)≤ 1≤ m+1 ⇒ −m≤(1/2) and m≥0 ⇒m≥0⇒ m≥1 if −1<m<1 ⇒−(1−m)≤(√(m^2 +2))≤m+1 ⇒ m^2 −2m +1 ≤m^2 +2 ≤m^2 +2m+1 ⇒ −m≤(1/2)and m≥0 ⇒m≥0 ⇒ 0≤m≤1 ∣t_2 ∣≤1 ⇒ ∣−m−(√(m^2 +2))∣≤1 ⇒ −1≤m+(√(m^2 +2))≤1 ⇒−m−1≤(√(m^2 +2))≤1−m so m≤1 if −m−1>0 ⇒m≤−1 ⇒ m^2 +2m+1≤m^2 +2≤m^2 −2m +1 ⇒ 2m+1≤2≤−2m+1 ⇒ 2m≤1≤−2m ⇒ m≤(1/2) and (1/2)≤−m ⇒m≤(1/2) and m≤−(1/2) ⇒ m≤−(1/2) ⇒m ≤−1 due to initial condition if −m−1≤0 ⇒−1≤m≤1 so ∣t_2 ∣ ≤1 ⇒ −1≤m≤1 finally ∣t_1 ∣≤1 and ∣t_2 ∣≤1 ⇒ 0≤m≤1 .

$${we}\:{have}\:{h}\left({x}\right)=\sqrt{\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}−\mathrm{2}{msinxcosx}} \\ $$$$=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−{msin}\left(\mathrm{2}{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\sqrt{\mathrm{2}−{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}{msin}\left(\mathrm{2}{x}\right)}\:{due}\:{to}\:{D}_{{f}} {we}\:{mist} \\ $$$${have}\:−{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}{msin}\left(\mathrm{2}{x}\right)+\mathrm{2}\geqslant\mathrm{0}\:\Rightarrow \\ $$$${sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:+\mathrm{2}{msin}\left(\mathrm{2}{x}\right)−\mathrm{2}\leqslant\mathrm{0}\:{let}\:{sin}\left(\mathrm{2}{x}\right)\:={t}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} +\mathrm{2}{mt}\:−\mathrm{2}\leqslant\mathrm{0}\:\:{and}\:\:\:\mid{t}\mid\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\Delta^{'} \:={m}^{\mathrm{2}} \:+\mathrm{2}>\mathrm{0}\Rightarrow{t}_{\mathrm{1}} =−{m}+\sqrt{{m}^{\mathrm{2}} +\mathrm{2}}\:\:{and}\: \\ $$$${t}_{\mathrm{2}} =−{m}−\sqrt{{m}^{\mathrm{2}\:} +\mathrm{2}}\:\: \\ $$$$\mid{t}_{\mathrm{1}} \mid\:\leqslant\mathrm{1}\:\Rightarrow\:−\mathrm{1}\leqslant−{m}+\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\leqslant\mathrm{1}\:\Rightarrow \\ $$$${m}−\mathrm{1}\:\leqslant\sqrt{{m}^{\mathrm{2}} +\mathrm{2}}\leqslant{m}+\mathrm{1}\:\:\:{if}\:{m}>\mathrm{1}\:\Rightarrow \\ $$$${m}^{\mathrm{2}} −\mathrm{2}{m}+\mathrm{1}\:\leqslant{m}^{\mathrm{2}} \:+\mathrm{2}\:\leqslant{m}^{\mathrm{2}} \:+\mathrm{2}{m}\:+\mathrm{2}\:\Rightarrow \\ $$$$−\mathrm{2}{m}+\mathrm{1}\leqslant\mathrm{2}\leqslant\mathrm{2}{m}+\mathrm{2}\:\Rightarrow\:−{m}+\frac{\mathrm{1}}{\mathrm{2}}\leqslant\:\mathrm{1}\leqslant\:{m}+\mathrm{1}\:\Rightarrow \\ $$$$−{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{m}\geqslant\mathrm{0}\:\Rightarrow{m}\geqslant\mathrm{0}\Rightarrow\:{m}\geqslant\mathrm{1} \\ $$$${if}\:−\mathrm{1}<{m}<\mathrm{1}\:\Rightarrow−\left(\mathrm{1}−{m}\right)\leqslant\sqrt{{m}^{\mathrm{2}} +\mathrm{2}}\leqslant{m}+\mathrm{1}\:\Rightarrow \\ $$$${m}^{\mathrm{2}} −\mathrm{2}{m}\:+\mathrm{1}\:\leqslant{m}^{\mathrm{2}} +\mathrm{2}\:\leqslant{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}\:\Rightarrow \\ $$$$−{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}}{and}\:{m}\geqslant\mathrm{0}\:\Rightarrow{m}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{0}\leqslant{m}\leqslant\mathrm{1} \\ $$$$\mid{t}_{\mathrm{2}} \mid\leqslant\mathrm{1}\:\Rightarrow\:\mid−{m}−\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\mid\leqslant\mathrm{1}\:\Rightarrow \\ $$$$−\mathrm{1}\leqslant{m}+\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\leqslant\mathrm{1}\:\Rightarrow−{m}−\mathrm{1}\leqslant\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\leqslant\mathrm{1}−{m}\:{so} \\ $$$${m}\leqslant\mathrm{1}\:\:{if}\:−{m}−\mathrm{1}>\mathrm{0}\:\Rightarrow{m}\leqslant−\mathrm{1}\:\Rightarrow \\ $$$${m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}\leqslant{m}^{\mathrm{2}} +\mathrm{2}\leqslant{m}^{\mathrm{2}} −\mathrm{2}{m}\:+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{2}{m}+\mathrm{1}\leqslant\mathrm{2}\leqslant−\mathrm{2}{m}+\mathrm{1}\:\Rightarrow\:\mathrm{2}{m}\leqslant\mathrm{1}\leqslant−\mathrm{2}{m}\:\Rightarrow \\ $$$${m}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant−{m}\:\Rightarrow{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{m}\leqslant−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${m}\leqslant−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{m}\:\leqslant−\mathrm{1}\:{due}\:{to}\:{initial}\:{condition} \\ $$$${if}\:−{m}−\mathrm{1}\leqslant\mathrm{0}\:\Rightarrow−\mathrm{1}\leqslant{m}\leqslant\mathrm{1}\:\:{so} \\ $$$$\mid{t}_{\mathrm{2}} \mid\:\leqslant\mathrm{1}\:\Rightarrow\:−\mathrm{1}\leqslant{m}\leqslant\mathrm{1}\:{finally} \\ $$$$\mid{t}_{\mathrm{1}} \mid\leqslant\mathrm{1}\:{and}\:\mid{t}_{\mathrm{2}} \mid\leqslant\mathrm{1}\:\Rightarrow\:\:\:\mathrm{0}\leqslant{m}\leqslant\mathrm{1}\:. \\ $$

Commented by math khazana by abdo last updated on 15/Aug/18

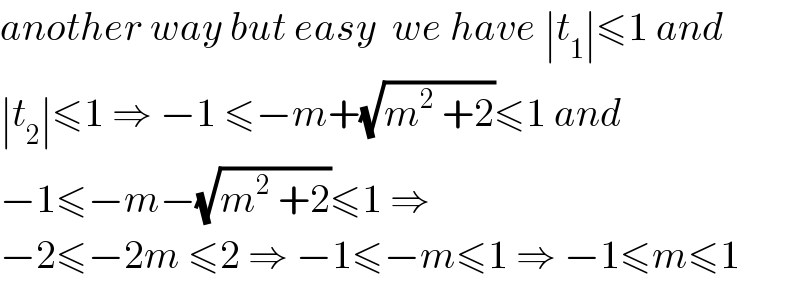
another way but easy we have ∣t_1 ∣≤1 and ∣t_2 ∣≤1 ⇒ −1 ≤−m+(√(m^2 +2))≤1 and −1≤−m−(√(m^2 +2))≤1 ⇒ −2≤−2m ≤2 ⇒ −1≤−m≤1 ⇒ −1≤m≤1

$${another}\:{way}\:{but}\:{easy}\:\:{we}\:{have}\:\mid{t}_{\mathrm{1}} \mid\leqslant\mathrm{1}\:{and} \\ $$$$\mid{t}_{\mathrm{2}} \mid\leqslant\mathrm{1}\:\Rightarrow\:−\mathrm{1}\:\leqslant−{m}+\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\leqslant\mathrm{1}\:{and} \\ $$$$−\mathrm{1}\leqslant−{m}−\sqrt{{m}^{\mathrm{2}} \:+\mathrm{2}}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$−\mathrm{2}\leqslant−\mathrm{2}{m}\:\leqslant\mathrm{2}\:\Rightarrow\:−\mathrm{1}\leqslant−{m}\leqslant\mathrm{1}\:\Rightarrow\:−\mathrm{1}\leqslant{m}\leqslant\mathrm{1} \\ $$

Commented by math khazana by abdo last updated on 15/Aug/18

−1≤m≤1

$$−\mathrm{1}\leqslant{m}\leqslant\mathrm{1} \\ $$

Commented by maxmathsup by imad last updated on 15/Aug/18

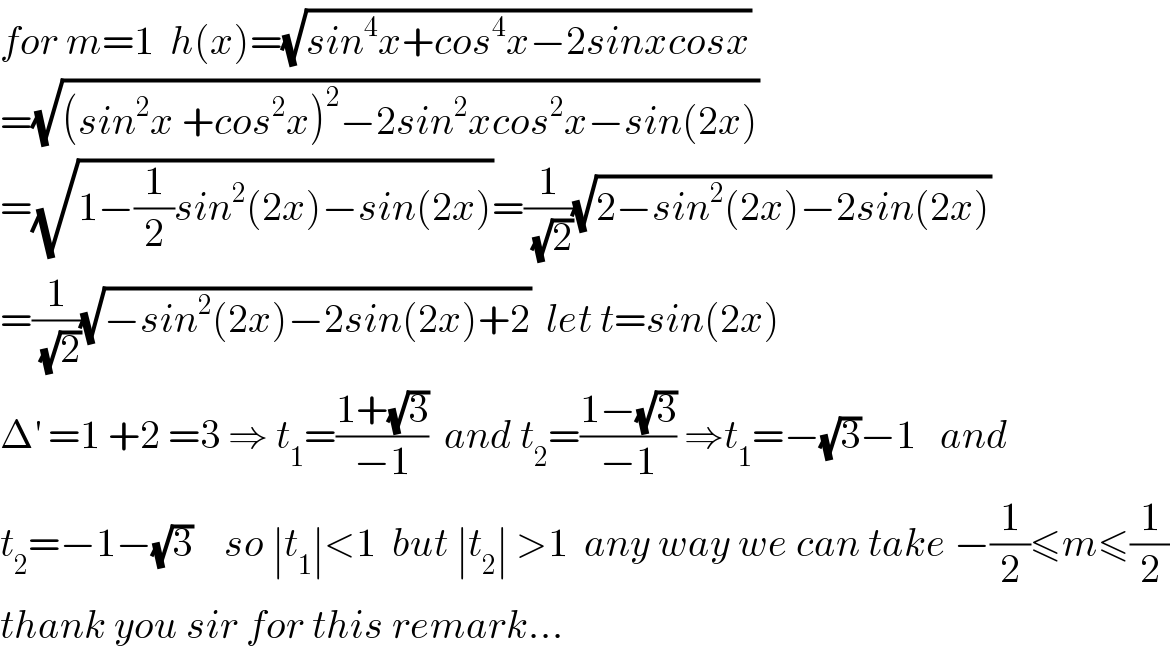
for m=1 h(x)=(√(sin^4 x+cos^4 x−2sinxcosx)) =(√((sin^2 x +cos^2 x)^2 −2sin^2 xcos^2 x−sin(2x))) =(√(1−(1/2)sin^2 (2x)−sin(2x)))=(1/(√2))(√(2−sin^2 (2x)−2sin(2x))) =(1/(√2))(√(−sin^2 (2x)−2sin(2x)+2)) let t=sin(2x) Δ^′ =1 +2 =3 ⇒ t_1 =((1+(√3))/(−1)) and t_2 =((1−(√3))/(−1)) ⇒t_1 =−(√3)−1 and t_2 =−1−(√3) so ∣t_1 ∣<1 but ∣t_2 ∣ >1 any way we can take −(1/2)≤m≤(1/2) thank you sir for this remark...

$${for}\:{m}=\mathrm{1}\:\:{h}\left({x}\right)=\sqrt{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}−\mathrm{2}{sinxcosx}} \\ $$$$=\sqrt{\left({sin}^{\mathrm{2}} {x}\:+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}−{sin}\left(\mathrm{2}{x}\right)} \\ $$$$=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\sqrt{\mathrm{2}−{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}{sin}\left(\mathrm{2}{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\sqrt{−{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}{sin}\left(\mathrm{2}{x}\right)+\mathrm{2}}\:\:{let}\:{t}={sin}\left(\mathrm{2}{x}\right) \\ $$$$\Delta^{'} \:=\mathrm{1}\:+\mathrm{2}\:=\mathrm{3}\:\Rightarrow\:{t}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{−\mathrm{1}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{−\mathrm{1}}\:\Rightarrow{t}_{\mathrm{1}} =−\sqrt{\mathrm{3}}−\mathrm{1}\:\:\:{and} \\ $$$${t}_{\mathrm{2}} =−\mathrm{1}−\sqrt{\mathrm{3}}\:\:\:\:{so}\:\mid{t}_{\mathrm{1}} \mid<\mathrm{1}\:\:{but}\:\mid{t}_{\mathrm{2}} \mid\:>\mathrm{1}\:\:{any}\:{way}\:{we}\:{can}\:{take}\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${thank}\:{you}\:{sir}\:{for}\:{this}\:{remark}... \\ $$

Answered by MJS last updated on 15/Aug/18

sin^4 x +cos^4 x −2msin x cos x ≥0 ...after some trigonometric transformations: (1/4)cos 4x −msin 2x +(3/4)≥0 (d/dx)[(1/4)cos 4x −msin 2x +(3/4)]=0 −sin 4x −2mcos 2x=0 x=arctan t ((2mt^4 +4t^3 −4t^2 −2m)/((t^2 +1)^2 ))=0 t^4 +((2t^3 )/m)−((2t)/m)−1=0 t=±1 ∨ t=−(1/m)±((√(1−m^2 ))/m) ⇒ −1≤m≤1 ⇒ x=±(π/4) ∨ x=arctan (−(1/m)±((√(1−m^2 ))/m)) (1/4)cos 4x −msin 2x +(3/4)≥0 x_1 =−(π/4) ⇒ m+(1/2)≥0 ⇒ m≥−(1/2) x_2 =(π/4) ⇒ −m+(1/2)≥0 ⇒ m≤(1/2) x_(3, 4) =arctan (−(1/m)±((√(1−m^2 ))/m)) ⇒ (m^2 /2)+1≥0 ⇒ m∈R answer is −(1/2)≤m≤(1/2)

$$\mathrm{sin}^{\mathrm{4}} \:{x}\:+\mathrm{cos}^{\mathrm{4}} \:{x}\:−\mathrm{2}{m}\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:\geqslant\mathrm{0} \\ $$$$...\mathrm{after}\:\mathrm{some}\:\mathrm{trigonometric}\:\mathrm{transformations}: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4}{x}\:−{m}\mathrm{sin}\:\mathrm{2}{x}\:+\frac{\mathrm{3}}{\mathrm{4}}\geqslant\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4}{x}\:−{m}\mathrm{sin}\:\mathrm{2}{x}\:+\frac{\mathrm{3}}{\mathrm{4}}\right]=\mathrm{0} \\ $$$$−\mathrm{sin}\:\mathrm{4}{x}\:−\mathrm{2}{m}\mathrm{cos}\:\mathrm{2}{x}=\mathrm{0} \\ $$$${x}=\mathrm{arctan}\:{t} \\ $$$$\frac{\mathrm{2}{mt}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}{m}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{2}{t}^{\mathrm{3}} }{{m}}−\frac{\mathrm{2}{t}}{{m}}−\mathrm{1}=\mathrm{0} \\ $$$${t}=\pm\mathrm{1}\:\vee\:{t}=−\frac{\mathrm{1}}{{m}}\pm\frac{\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }}{{m}}\:\Rightarrow\:−\mathrm{1}\leqslant{m}\leqslant\mathrm{1} \\ $$$$\Rightarrow\:{x}=\pm\frac{\pi}{\mathrm{4}}\:\vee\:{x}=\mathrm{arctan}\:\left(−\frac{\mathrm{1}}{{m}}\pm\frac{\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }}{{m}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4}{x}\:−{m}\mathrm{sin}\:\mathrm{2}{x}\:+\frac{\mathrm{3}}{\mathrm{4}}\geqslant\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\frac{\pi}{\mathrm{4}}\:\Rightarrow\:{m}+\frac{\mathrm{1}}{\mathrm{2}}\geqslant\mathrm{0}\:\Rightarrow\:{m}\geqslant−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} =\frac{\pi}{\mathrm{4}}\:\Rightarrow\:−{m}+\frac{\mathrm{1}}{\mathrm{2}}\geqslant\mathrm{0}\:\Rightarrow\:{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\mathrm{arctan}\:\left(−\frac{\mathrm{1}}{{m}}\pm\frac{\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }}{{m}}\right)\:\Rightarrow\:\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow\:{m}\in\mathbb{R} \\ $$$$\mathrm{answer}\:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by lucha116 last updated on 15/Aug/18

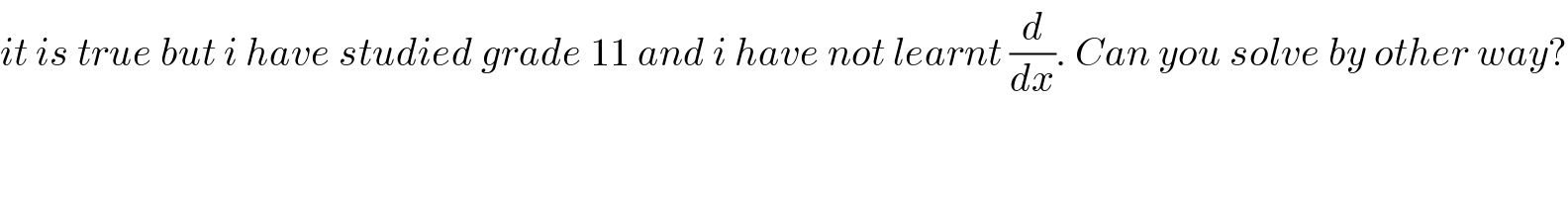
it is true but i have studied grade 11 and i have not learnt (d/dx). Can you solve by other way?

$${it}\:{is}\:{true}\:{but}\:{i}\:{have}\:{studied}\:{grade}\:\mathrm{11}\:{and}\:{i}\:{have}\:{not}\:{learnt}\:\frac{{d}}{{dx}}.\:{Can}\:{you}\:{solve}\:{by}\:{other}\:{way}? \\ $$

Commented by maxmathsup by imad last updated on 15/Aug/18

this question is more difficult for grade 11 and generally the consept of trigonometry is more difficult ...

$${this}\:{question}\:{is}\:{more}\:{difficult}\:{for}\:{grade}\:\mathrm{11}\:{and}\:{generally}\:{the}\:{consept}\:{of}\: \\ $$$${trigonometry}\:{is}\:{more}\:{difficult}\:\:... \\ $$

Commented by lucha116 last updated on 15/Aug/18

yes. i know. thks ^� 0 ^�

$${yes}.\:{i}\:{know}.\:{thks}\hat {\:}\mathrm{0}\hat {\:} \\ $$

Answered by MJS last updated on 15/Aug/18

hopefully an easier explanation sin^2 x =(1/2)(1−cos 2x) cos^2 x =(1/2)(1+cos 2x) sin^4 x =((1/2)(1−cos 2x))^2 = =(1/4)(1−2cos 2x +cos^2 2x)= =(1/4)(1−2cos 2x +(1/2)(1+cos 4x))= =(3/8)+(1/8)cos 4x −(1/2)cos 2x similar cos^4 x =(3/8)+(1/8)cos 4x +(1/2)cos 2x ⇒ sin^4 x +cos^4 x =(3/4)+(1/4)cos 4x this has a period of (π/2) with min= ((((π/4)+(π/2)z)),((1/2)) ) ; z∈Z −2msin x cos x =−msin 2x this has a period of π with min= ((( (π/4)+πz)),((−m)) ) ; z∈Z the sum of both gives (((π/4)),(((1/2)−m)) ) within the first period. we know that (1/2)−m≥0 ⇒ m≤(1/2) if m<0 the min of −msin 2x changes to the 2^(nd) half of its period because the curve now is upside down: min= (((((3π)/4)+πz)),(m) ) so the sum now is ((((3π)/4)),(((1/2)+m)) ) ⇒ m≥−(1/2)

$$\mathrm{hopefully}\:\mathrm{an}\:\mathrm{easier}\:\mathrm{explanation} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\right)^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{2cos}\:\mathrm{2}{x}\:+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{2cos}\:\mathrm{2}{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}\right)\right)= \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\:\mathrm{4}{x}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\mathrm{similar}\:\mathrm{cos}^{\mathrm{4}} \:{x}\:=\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\:\mathrm{4}{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\Rightarrow\:\mathrm{sin}^{\mathrm{4}} \:{x}\:+\mathrm{cos}^{\mathrm{4}} \:{x}\:=\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4}{x} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{a}\:\mathrm{period}\:\mathrm{of}\:\frac{\pi}{\mathrm{2}}\:\mathrm{with}\:\mathrm{min}=\begin{pmatrix}{\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}{z}}\\{\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix}\:;\:{z}\in\mathbb{Z} \\ $$$$−\mathrm{2}{m}\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:=−{m}\mathrm{sin}\:\mathrm{2}{x} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{a}\:\mathrm{period}\:\mathrm{of}\:\pi\:\mathrm{with}\:\mathrm{min}=\begin{pmatrix}{\:\frac{\pi}{\mathrm{4}}+\pi{z}}\\{−{m}}\end{pmatrix}\:;\:{z}\in\mathbb{Z} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{both}\:\mathrm{gives}\:\begin{pmatrix}{\frac{\pi}{\mathrm{4}}}\\{\frac{\mathrm{1}}{\mathrm{2}}−{m}}\end{pmatrix}\:\mathrm{within}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{period}.\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\frac{\mathrm{1}}{\mathrm{2}}−{m}\geqslant\mathrm{0}\:\Rightarrow\:{m}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{if}\:{m}<\mathrm{0}\:\mathrm{the}\:\mathrm{min}\:\mathrm{of}\:−{m}\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{changes}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{half}\:\mathrm{of}\:\mathrm{its}\:\mathrm{period}\:\mathrm{because}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{now} \\ $$$$\mathrm{is}\:\mathrm{upside}\:\mathrm{down}:\:\mathrm{min}=\begin{pmatrix}{\frac{\mathrm{3}\pi}{\mathrm{4}}+\pi{z}}\\{{m}}\end{pmatrix} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{now}\:\mathrm{is}\:\begin{pmatrix}{\frac{\mathrm{3}\pi}{\mathrm{4}}}\\{\frac{\mathrm{1}}{\mathrm{2}}+{m}}\end{pmatrix}\:\:\Rightarrow\:{m}\geqslant−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com