
Question and Answers Forum
Question Number 41913 by math khazana by abdo last updated on 15/Aug/18
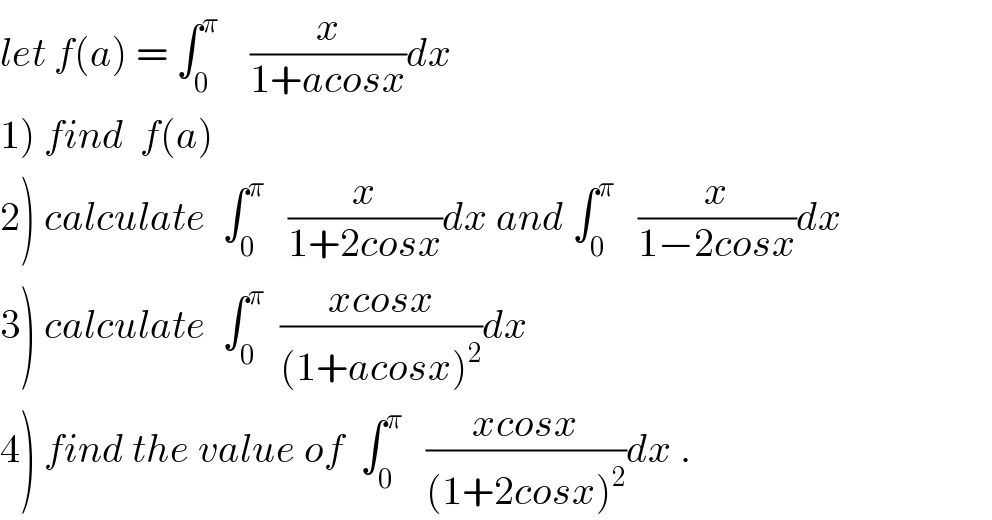
Answered by maxmathsup by imad last updated on 16/Aug/18
![1) we have f(a) = ∫_0 ^π (x/(1+a((2tan((x/2)))/(1+tan^2 ((x/2)))))) dx changement tan((x/2)) =t give f(a) =∫_0 ^∞ ((2arctan(t))/(1+((2at)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^∞ ((4arctan(t))/(1+t^2 +2at))dt =∫_0 ^∞ ((4arctan(t))/(t^2 +2at +1)) dt =4 ∫_0 ^∞ ((arctan(t))/(t^2 +2at +1))dt =w(1) with w(α) =∫_0 ^∞ ((arctan(αt))/(t^2 +2at +1)) dt we have w^′ (α) =∫_0 ^∞ (t/((1+α^2 t^2 )(t^2 +2at +1))) dt =_(αt =u) ∫_0 ^∞ (u/(α(1+u^2 )((u^2 /α^2 ) +2a(u/α)+1)))(du/α) = ∫_0 ^∞ ((udu)/(α^2 (1+u^2 )(((u^2 +2αau +α^2 )/α^2 )))) =∫_0 ^∞ ((udu)/((u^2 +1)(u^2 +2αau +α^2 ))) let decompose F(u) = (u/((u^2 +1)(u^2 +2αau +α^2 ))) (let take α>0) roots of u^2 +2αau +α^2 Δ^′ =α^2 a^2 −α^2 =α^2 (a^2 −1) case1) ∣a∣>1 ⇒ u_1 =−αa +∣α∣(√(a^2 −1)) and u_2 =−αa −∣α∣(√(a^2 −1)) F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) =(u/((u−u_1 )(u−u_2 )(u^2 +1))) a = (u_1 /((u_1 −u_2 )(u_1 ^2 +1))) =((∣α∣(√(a^2 −1))−αa)/(2∣α∣(√(a^2 −1))((∣α∣(√(a^2 −1))−αa)^2 +1))) =((α((√(a^2 −1))−a))/(2α(√(a^2 −1))(α^2 ((√(a^2 −1))−a)^2 +1))) =(((√(a^2 −1))−a)/(2(√(a^2 −1)){α^2 ((√(a^2 −1))−a)^2 +1})) b = (u_2 /((u_2 −u_1 )(u_2 ^2 +1))) = ((−α(a+(√(a^2 −1))))/(−2α(√(a^2 −1)){ α^2 (a+(√(a^2 −1)))^2 +1})) lim_(u→+∞) u F(u) =0 =a+b +c ⇒ c =−a−b ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +d)/(u^2 +1)) F(0) =0 =−(a/u_1 ) −(b/u_2 ) +d ⇒ d =(a/u_1 ) +(b/u_2 ) ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +(a/u_1 )+(b/u_2 ))/(u^2 +1)) ⇒ ∫_0 ^∞ F(u)du =[aln∣u−u_1 ∣ +bln∣u−u_2 ∣]_0 ^(+∞) −[((a+b)/2)ln(u^2 +1)]_0 ^(+∞) +((a/u_1 ) +(b/u_2 ))[ arctan(u)]_0 ^(+∞) =[ ln(∣u−u_1 ∣^a ∣u−u_2 ∣^b )−ln((u^2 +1)^((a+b)/2) )]_0 ^(+∞) +(π/2){(a/u_1 ) +(b/u_2 )} ...be continued...](Q42018.png)
| ||
Question and Answers Forum | ||
Question Number 41913 by math khazana by abdo last updated on 15/Aug/18 | ||
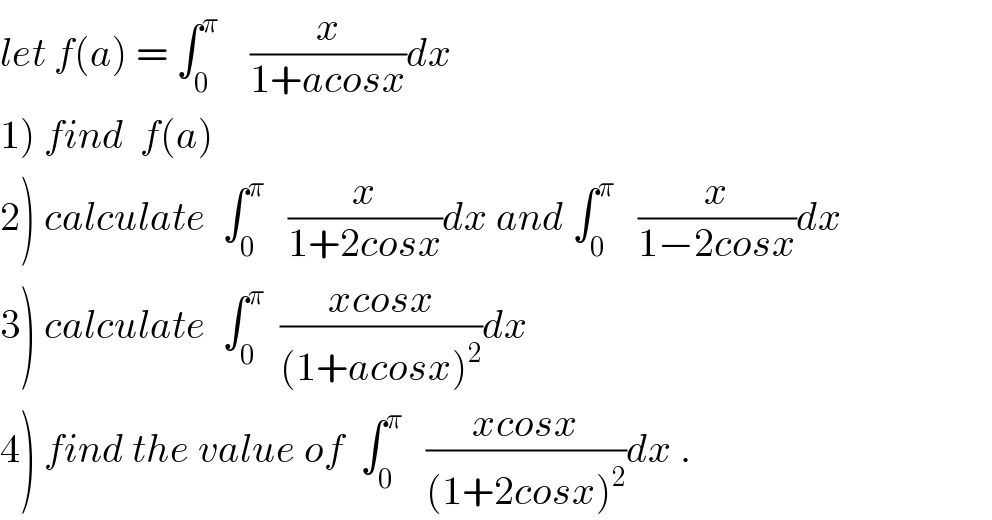 | ||
Answered by maxmathsup by imad last updated on 16/Aug/18 | ||
![1) we have f(a) = ∫_0 ^π (x/(1+a((2tan((x/2)))/(1+tan^2 ((x/2)))))) dx changement tan((x/2)) =t give f(a) =∫_0 ^∞ ((2arctan(t))/(1+((2at)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^∞ ((4arctan(t))/(1+t^2 +2at))dt =∫_0 ^∞ ((4arctan(t))/(t^2 +2at +1)) dt =4 ∫_0 ^∞ ((arctan(t))/(t^2 +2at +1))dt =w(1) with w(α) =∫_0 ^∞ ((arctan(αt))/(t^2 +2at +1)) dt we have w^′ (α) =∫_0 ^∞ (t/((1+α^2 t^2 )(t^2 +2at +1))) dt =_(αt =u) ∫_0 ^∞ (u/(α(1+u^2 )((u^2 /α^2 ) +2a(u/α)+1)))(du/α) = ∫_0 ^∞ ((udu)/(α^2 (1+u^2 )(((u^2 +2αau +α^2 )/α^2 )))) =∫_0 ^∞ ((udu)/((u^2 +1)(u^2 +2αau +α^2 ))) let decompose F(u) = (u/((u^2 +1)(u^2 +2αau +α^2 ))) (let take α>0) roots of u^2 +2αau +α^2 Δ^′ =α^2 a^2 −α^2 =α^2 (a^2 −1) case1) ∣a∣>1 ⇒ u_1 =−αa +∣α∣(√(a^2 −1)) and u_2 =−αa −∣α∣(√(a^2 −1)) F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) =(u/((u−u_1 )(u−u_2 )(u^2 +1))) a = (u_1 /((u_1 −u_2 )(u_1 ^2 +1))) =((∣α∣(√(a^2 −1))−αa)/(2∣α∣(√(a^2 −1))((∣α∣(√(a^2 −1))−αa)^2 +1))) =((α((√(a^2 −1))−a))/(2α(√(a^2 −1))(α^2 ((√(a^2 −1))−a)^2 +1))) =(((√(a^2 −1))−a)/(2(√(a^2 −1)){α^2 ((√(a^2 −1))−a)^2 +1})) b = (u_2 /((u_2 −u_1 )(u_2 ^2 +1))) = ((−α(a+(√(a^2 −1))))/(−2α(√(a^2 −1)){ α^2 (a+(√(a^2 −1)))^2 +1})) lim_(u→+∞) u F(u) =0 =a+b +c ⇒ c =−a−b ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +d)/(u^2 +1)) F(0) =0 =−(a/u_1 ) −(b/u_2 ) +d ⇒ d =(a/u_1 ) +(b/u_2 ) ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +(a/u_1 )+(b/u_2 ))/(u^2 +1)) ⇒ ∫_0 ^∞ F(u)du =[aln∣u−u_1 ∣ +bln∣u−u_2 ∣]_0 ^(+∞) −[((a+b)/2)ln(u^2 +1)]_0 ^(+∞) +((a/u_1 ) +(b/u_2 ))[ arctan(u)]_0 ^(+∞) =[ ln(∣u−u_1 ∣^a ∣u−u_2 ∣^b )−ln((u^2 +1)^((a+b)/2) )]_0 ^(+∞) +(π/2){(a/u_1 ) +(b/u_2 )} ...be continued...](Q42018.png) | ||
| ||