
Question and Answers Forum
Question Number 42085 by maxmathsup by imad last updated on 17/Aug/18
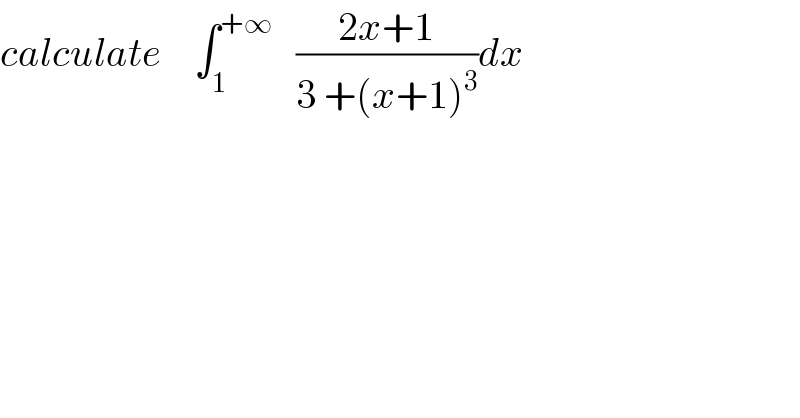
Commented by maxmathsup by imad last updated on 18/Aug/18
![let A = ∫_1 ^(+∞) ((2x+1)/(3+(x+1)^3 )) dx changement x+1 =t give A = ∫_2 ^(+∞) ((2(t−1) +1)/(3 +t^3 )) dt = ∫_2 ^(+∞) ((2t−1)/(t^3 +3)) dt also changement^3 (√3)u =t give A = ∫_(2/3_(√3) ) ^(+∞) ((2(^3 (√3))u−1)/(3(1+u^3 )))^3 (√3)du let α =(2/((^3 (√3)))) = (2/3) (^3 (√3))^2 ∫_α ^(+∞) (u/(u^3 +1)) −^3 (√3) ∫_α ^(+∞) (du/(u^3 +1)) =(2/3)((2/α))^2 ∫_α ^(+∞) (u/(u^3 +1))du −(2/α) ∫_α ^(+∞) (du/(u^3 +1)) = ∫_α ^(+∞) (((8/(3α^2 ))u −(2/α))/(u^3 +1)) du =(2/α) ∫_α ^(+∞) (((4/(3α))u −1)/(u^3 +1)) du = (2/(3α^2 )) ∫_α ^(+∞) ((4u−3α)/(u^3 +1)) du let decompose F(u) =((4u−3α)/(u^3 +1)) F(u) =((4u−3α)/((u+1)(u^2 −u+1))) = (a/(u+1)) +((bu +c)/(u^2 −u +1)) a =lim_(u→−1) (u+1)F(u)=((−4−3α)/3) lim_(u→+∞) u F(u) =0 =a+b ⇒ b =((4+3α)/3) ⇒ F(u) =−((3α+4)/(3(u+1))) +(1/3) (((3α+4)u +3c)/(u^2 −u +1)) F(0) =−3α =−((3α+4)/3) +c ⇒c =−3α +((3α+4)/3) =((−6α +4)/3) ⇒ F(u) = −((3α+4)/(3(u+1))) +(1/3) (((3α+4)u −6α +4)/(u^2 −u +1)) ⇒ ∫_α ^(+∞) F(u)du =(−α−(4/3)) ∫_α ^(+∞) (du/(u+1)) +((3α+4)/6) ∫_α ^(+∞) ((2α−1+1)/(u^2 −u+1))du +((4−6α)/3) ∫_α ^(+∞) (du/(u^2 −u +1)) =[(−α−(4/3))ln∣u+1∣ +((3α+4)/6)ln(u^2 −u+1)]_0 ^(+∞) +((4−6α)/3) ∫_α ^(+∞) (du/(u^2 −u +1)) ...](Q42120.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Aug/18

| ||
Question and Answers Forum | ||
Question Number 42085 by maxmathsup by imad last updated on 17/Aug/18 | ||
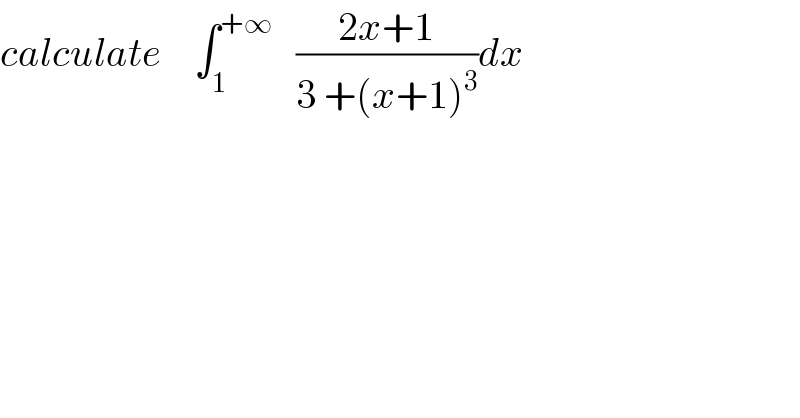 | ||
Commented by maxmathsup by imad last updated on 18/Aug/18 | ||
![let A = ∫_1 ^(+∞) ((2x+1)/(3+(x+1)^3 )) dx changement x+1 =t give A = ∫_2 ^(+∞) ((2(t−1) +1)/(3 +t^3 )) dt = ∫_2 ^(+∞) ((2t−1)/(t^3 +3)) dt also changement^3 (√3)u =t give A = ∫_(2/3_(√3) ) ^(+∞) ((2(^3 (√3))u−1)/(3(1+u^3 )))^3 (√3)du let α =(2/((^3 (√3)))) = (2/3) (^3 (√3))^2 ∫_α ^(+∞) (u/(u^3 +1)) −^3 (√3) ∫_α ^(+∞) (du/(u^3 +1)) =(2/3)((2/α))^2 ∫_α ^(+∞) (u/(u^3 +1))du −(2/α) ∫_α ^(+∞) (du/(u^3 +1)) = ∫_α ^(+∞) (((8/(3α^2 ))u −(2/α))/(u^3 +1)) du =(2/α) ∫_α ^(+∞) (((4/(3α))u −1)/(u^3 +1)) du = (2/(3α^2 )) ∫_α ^(+∞) ((4u−3α)/(u^3 +1)) du let decompose F(u) =((4u−3α)/(u^3 +1)) F(u) =((4u−3α)/((u+1)(u^2 −u+1))) = (a/(u+1)) +((bu +c)/(u^2 −u +1)) a =lim_(u→−1) (u+1)F(u)=((−4−3α)/3) lim_(u→+∞) u F(u) =0 =a+b ⇒ b =((4+3α)/3) ⇒ F(u) =−((3α+4)/(3(u+1))) +(1/3) (((3α+4)u +3c)/(u^2 −u +1)) F(0) =−3α =−((3α+4)/3) +c ⇒c =−3α +((3α+4)/3) =((−6α +4)/3) ⇒ F(u) = −((3α+4)/(3(u+1))) +(1/3) (((3α+4)u −6α +4)/(u^2 −u +1)) ⇒ ∫_α ^(+∞) F(u)du =(−α−(4/3)) ∫_α ^(+∞) (du/(u+1)) +((3α+4)/6) ∫_α ^(+∞) ((2α−1+1)/(u^2 −u+1))du +((4−6α)/3) ∫_α ^(+∞) (du/(u^2 −u +1)) =[(−α−(4/3))ln∣u+1∣ +((3α+4)/6)ln(u^2 −u+1)]_0 ^(+∞) +((4−6α)/3) ∫_α ^(+∞) (du/(u^2 −u +1)) ...](Q42120.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Aug/18 | ||
 | ||
| ||