
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 42098 by abdo.msup.com last updated on 17/Aug/18
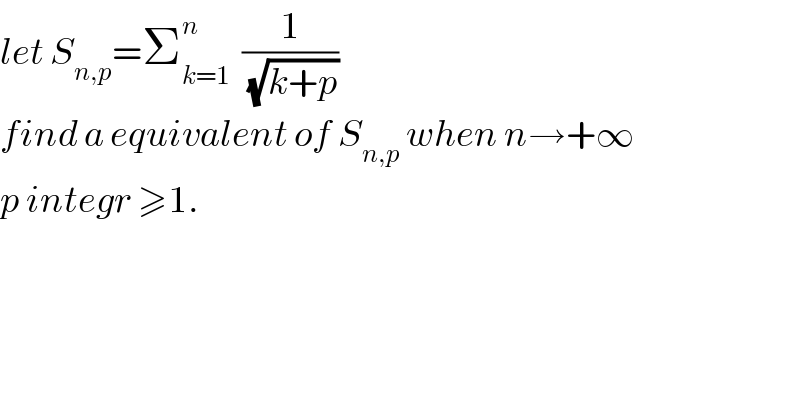
Commented by maxmathsup by imad last updated on 18/Aug/18
![the sequence ((1/(√k)))_(k≥1) is decreasing ⇒ ∫_k ^(k+1) (dt/(√(t+p))) ≤ (1/(√(k+p))) ≤ ∫_(k−1) ^k (dt/(√(t+p))) ⇒ Σ_(k=1) ^n ∫_k ^(k+1) (dt/(√(t+p))) ≤Σ_(k=1) ^n (1/(√(k+p))) ≤ Σ_(k=1) ^n ∫_(k−1) ^k (dt/(√(t+p))) ⇒ ∫_1 ^(n+1) (dt/(√(t+p))) ≤ S_(n,p) ≤ ∫_0 ^n (dt/(√(t+p))) ⇒ [2(√(t+p))]_1 ^(n+1) ≤S_(n,p) ≤[2(√(t+p))]_0 ^n ⇒ 2(√(n+1+p)) −2(√(p+1)) ≤ S_(n,p) ≤ 2(√(n+p)) −2(√(p )) ⇒ ((2(√(n+1+p))−2(√(p+1)))/(2(√(n+p)))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ ((2(√(n+p)) −2(√p))/(2(√(n+p)))) ⇒ (√(1+(1/(n+p))))−(√((p+1)/(n+p))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ 1−(√(p/(n+p))) but lim_(n→+∞ ) (√(1+(1/(n+p))))−(√((p+1)/(n+1))) =1 and lim_(n→+∞) 1−(√(p/(n+p))) =1 ⇒ S_(n,p) ∼ 2(√(n+p)) (n→+∞ and p fixed)](Q42130.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 42098 by abdo.msup.com last updated on 17/Aug/18 | ||
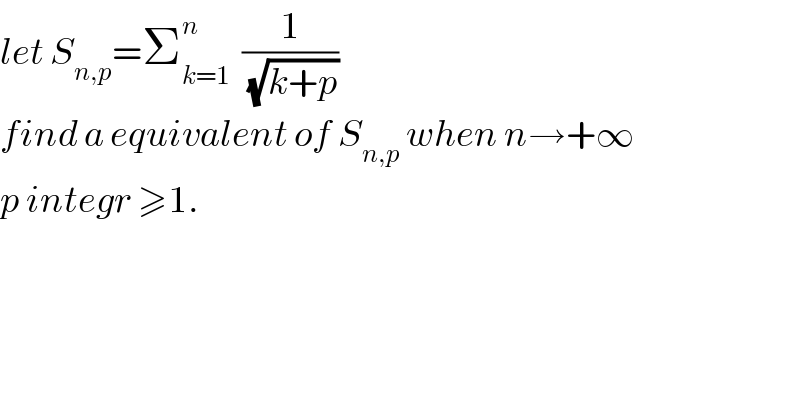 | ||
Commented by maxmathsup by imad last updated on 18/Aug/18 | ||
![the sequence ((1/(√k)))_(k≥1) is decreasing ⇒ ∫_k ^(k+1) (dt/(√(t+p))) ≤ (1/(√(k+p))) ≤ ∫_(k−1) ^k (dt/(√(t+p))) ⇒ Σ_(k=1) ^n ∫_k ^(k+1) (dt/(√(t+p))) ≤Σ_(k=1) ^n (1/(√(k+p))) ≤ Σ_(k=1) ^n ∫_(k−1) ^k (dt/(√(t+p))) ⇒ ∫_1 ^(n+1) (dt/(√(t+p))) ≤ S_(n,p) ≤ ∫_0 ^n (dt/(√(t+p))) ⇒ [2(√(t+p))]_1 ^(n+1) ≤S_(n,p) ≤[2(√(t+p))]_0 ^n ⇒ 2(√(n+1+p)) −2(√(p+1)) ≤ S_(n,p) ≤ 2(√(n+p)) −2(√(p )) ⇒ ((2(√(n+1+p))−2(√(p+1)))/(2(√(n+p)))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ ((2(√(n+p)) −2(√p))/(2(√(n+p)))) ⇒ (√(1+(1/(n+p))))−(√((p+1)/(n+p))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ 1−(√(p/(n+p))) but lim_(n→+∞ ) (√(1+(1/(n+p))))−(√((p+1)/(n+1))) =1 and lim_(n→+∞) 1−(√(p/(n+p))) =1 ⇒ S_(n,p) ∼ 2(√(n+p)) (n→+∞ and p fixed)](Q42130.png) | ||