
Question Number 42191 by maxmathsup by imad last updated on 19/Aug/18
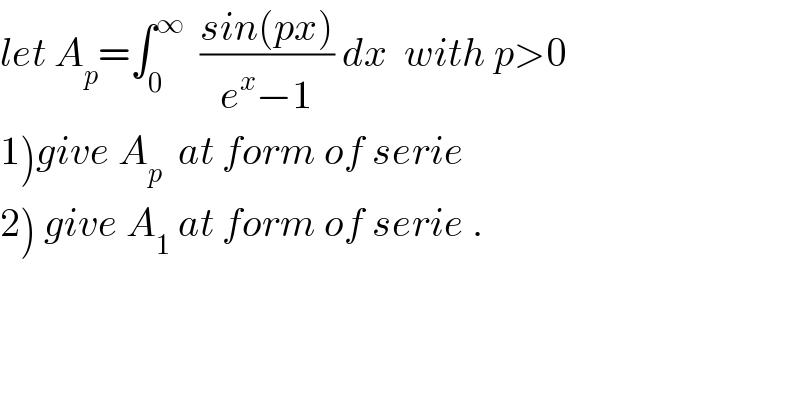
$${let}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({px}\right)}{{e}^{{x}} −\mathrm{1}}\:{dx}\:\:{with}\:{p}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right){give}\:{A}_{{p}} \:\:{at}\:{form}\:{of}\:{serie} \\ $$ $$\left.\mathrm{2}\right)\:{give}\:{A}_{\mathrm{1}} \:{at}\:{form}\:{of}\:{serie}\:. \\ $$
Commented bymaxmathsup by imad last updated on 20/Aug/18
![1) we have A_p =∫_0 ^∞ ((e^(−x) sin(px))/(1−e^(−x) )) dx =∫_0 ^∞ (Σ_(n=0) ^∞ e^(−nx) )e^(−x) sin(px))dx =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)x) sin(px) dx =_((n+1)x =t) Σ_(n=0) ^∞ ∫_0 ^∞ e^(−t) sin(p(t/(n+1)))(dt/(n+1)) = Σ_(n=0) ^∞ (1/(n+1)) ∫_0 ^∞ e^(−t) sin((p/(n+1))t)dt let calculate I_λ =∫_0 ^∞ e^(−t) sin(λt) dt ⇒I_λ = Im(∫_0 ^∞ e^(−t+iλt) dt) but ∫_0 ^∞ e^((−1+iλ)t) dt =[ (1/(−1+iλ)) e^((−1+iλ)t) ]_0 ^∞ =−(1/(−1+iλ)) =(1/(1−iλ)) =((1+iλ)/(1+λ^2 )) ⇒ I_λ =(λ/(1+λ^2 )) ⇒ A_p =Σ_(n=0) ^∞ (1/(n+1))(((p/(n+1))/(1+((p/(n+1)))^2 ))) = Σ_(n=0) ^∞ (1/(n+1))((p/(n+1))(((n+1)^2 )/((n+1)^2 +p^2 )))= Σ_(n=0) ^∞ (p/((n+1)^2 +p^2 )) ⇒ A_p =Σ_(n=0) ^∞ (p/((n+1)^2 +p^2 )) 2) A_1 =Σ_(n=0) ^∞ (1/((n+1)^2 +1)) = Σ_(n=1) ^∞ (1/(n^2 +1)) .](Q42220.png)
$$\left.\mathrm{1}\left.\right)\:{we}\:{have}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{x}} \:{sin}\left({px}\right)}{\mathrm{1}−{e}^{−{x}} }\:{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \right){e}^{−{x}} {sin}\left({px}\right)\right){dx} \\ $$ $$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({n}+\mathrm{1}\right){x}} {sin}\left({px}\right)\:{dx}\:=_{\left({n}+\mathrm{1}\right){x}\:={t}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}} {sin}\left({p}\frac{{t}}{{n}+\mathrm{1}}\right)\frac{{dt}}{{n}+\mathrm{1}} \\ $$ $$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−{t}} \:\:{sin}\left(\frac{{p}}{{n}+\mathrm{1}}{t}\right){dt}\:\:{let}\:{calculate} \\ $$ $${I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}} \:{sin}\left(\lambda{t}\right)\:{dt}\:\Rightarrow{I}_{\lambda} =\:{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}+{i}\lambda{t}} {dt}\right)\:\:{but} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−\mathrm{1}+{i}\lambda\right){t}} {dt}\:=\left[\:\frac{\mathrm{1}}{−\mathrm{1}+{i}\lambda}\:{e}^{\left(−\mathrm{1}+{i}\lambda\right){t}} \right]_{\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{−\mathrm{1}+{i}\lambda}\:=\frac{\mathrm{1}}{\mathrm{1}−{i}\lambda} \\ $$ $$=\frac{\mathrm{1}+{i}\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow\:{I}_{\lambda} =\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow\:{A}_{{p}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\frac{\frac{{p}}{{n}+\mathrm{1}}}{\mathrm{1}+\left(\frac{{p}}{{n}+\mathrm{1}}\right)^{\mathrm{2}} }\right) \\ $$ $$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\frac{{p}}{{n}+\mathrm{1}}\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+{p}^{\mathrm{2}} }\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{{p}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+{p}^{\mathrm{2}} }\:\Rightarrow \\ $$ $${A}_{{p}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{p}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+{p}^{\mathrm{2}} } \\ $$ $$\left.\mathrm{2}\right)\:\:{A}_{\mathrm{1}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\:\:. \\ $$ $$ \\ $$ $$ \\ $$
