Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 42493 by maxmathsup by imad last updated on 26/Aug/18

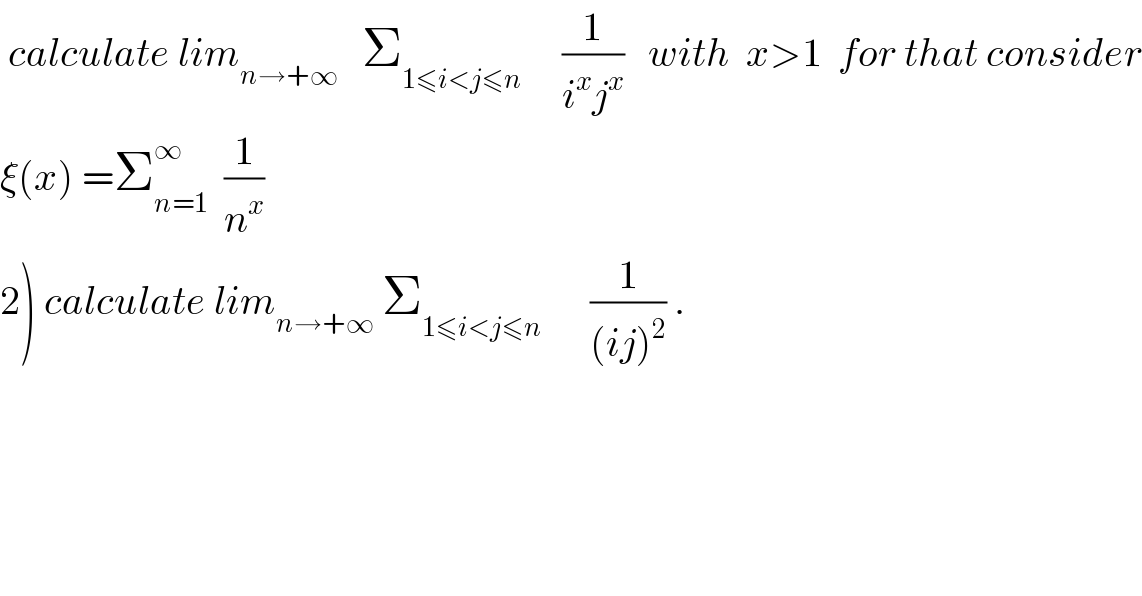
calculate lim_(n→+∞) Σ_(1≤i<j≤n) (1/(i^x j^x )) with x>1 for that consider ξ(x) =Σ_(n=1) ^∞ (1/n^x ) 2) calculate lim_(n→+∞) Σ_(1≤i<j≤n) (1/((ij)^2 )) .

$$\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\:\frac{\mathrm{1}}{{i}^{{x}} {j}^{{x}} }\:\:\:{with}\:\:{x}>\mathrm{1}\:\:{for}\:{that}\:{consider} \\ $$ $$\xi\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{{x}} } \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\:\:\frac{\mathrm{1}}{\left({ij}\right)^{\mathrm{2}} }\:. \\ $$

Commented bymaxmathsup by imad last updated on 29/Aug/18

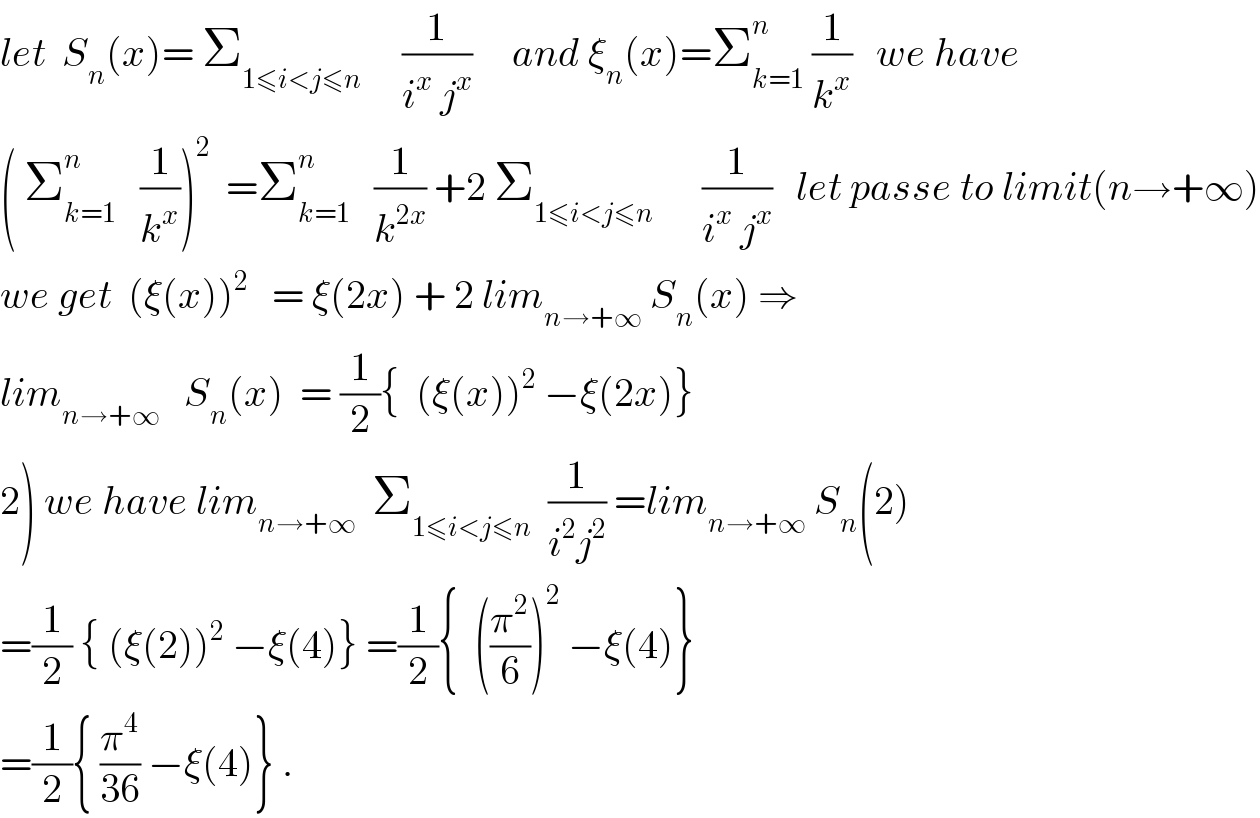
let S_n (x)= Σ_(1≤i<j≤n) (1/(i^x j^x )) and ξ_n (x)=Σ_(k=1) ^n (1/k^x ) we have ( Σ_(k=1) ^n (1/k^x ))^2 =Σ_(k=1) ^n (1/k^(2x) ) +2 Σ_(1≤i<j≤n) (1/(i^x j^x )) let passe to limit(n→+∞) we get (ξ(x))^2 = ξ(2x) + 2 lim_(n→+∞) S_n (x) ⇒ lim_(n→+∞) S_n (x) = (1/2){ (ξ(x))^2 −ξ(2x)} 2) we have lim_(n→+∞) Σ_(1≤i<j≤n) (1/(i^2 j^2 )) =lim_(n→+∞) S_n (2) =(1/2) { (ξ(2))^2 −ξ(4)} =(1/2){ ((π^2 /6))^2 −ξ(4)} =(1/2){ (π^4 /(36)) −ξ(4)} .

$${let}\:\:{S}_{{n}} \left({x}\right)=\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\:\frac{\mathrm{1}}{{i}^{{x}} \:{j}^{{x}} }\:\:\:\:\:{and}\:\xi_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{{x}} }\:\:\:{we}\:{have}\: \\ $$ $$\left(\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{k}^{{x}} }\right)^{\mathrm{2}} \:\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}{x}} }\:+\mathrm{2}\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\:\:\frac{\mathrm{1}}{{i}^{{x}} \:{j}^{{x}} }\:\:\:{let}\:{passe}\:{to}\:{limit}\left({n}\rightarrow+\infty\right) \\ $$ $${we}\:{get}\:\:\left(\xi\left({x}\right)\right)^{\mathrm{2}} \:\:\:=\:\xi\left(\mathrm{2}{x}\right)\:+\:\mathrm{2}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \left({x}\right)\:\Rightarrow \\ $$ $${lim}_{{n}\rightarrow+\infty} \:\:\:{S}_{{n}} \left({x}\right)\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\left(\xi\left({x}\right)\right)^{\mathrm{2}} \:−\xi\left(\mathrm{2}{x}\right)\right\} \\ $$ $$\left.\mathrm{2}\right)\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\frac{\mathrm{1}}{{i}^{\mathrm{2}} {j}^{\mathrm{2}} }\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \left(\mathrm{2}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\:\left(\xi\left(\mathrm{2}\right)\right)^{\mathrm{2}} \:−\xi\left(\mathrm{4}\right)\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right)^{\mathrm{2}} \:−\xi\left(\mathrm{4}\right)\right\} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\pi^{\mathrm{4}} }{\mathrm{36}}\:−\xi\left(\mathrm{4}\right)\right\}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com