
Question and Answers Forum
Question Number 42503 by maxmathsup by imad last updated on 26/Aug/18
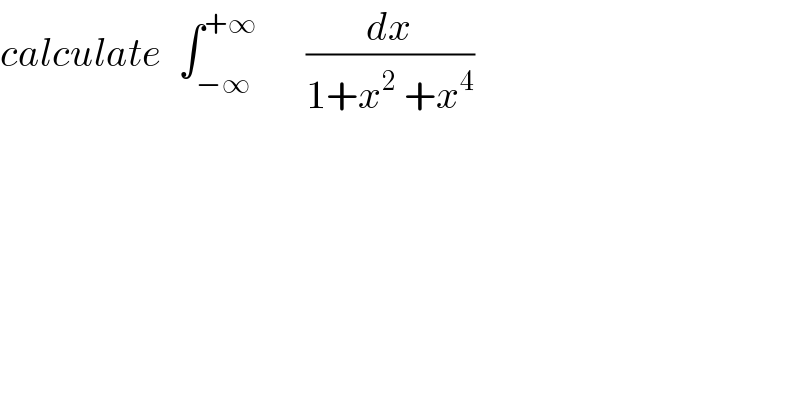
Commented by maxmathsup by imad last updated on 27/Aug/18

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18
![∫_(−∞) ^∞ ((1/x^2 )/(x^2 +(1/x^2 )+1))dx (1/2)∫_(−∞) ^∞ ((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )+1))dx (1/2)[∫_(−∞) ^∞ ((d(x−(1/x)))/((x−(1/x))^2 +3))−∫_(−∞) ^∞ ((d(x+(1/x)))/((x+(1/x))^2 −1))] (1/2)[∣(1/(√3))tan^(−1) (((x−(1/x))/(√3)))∣_(−∞) ^∞ −(1/(2×1))∣ln(((x+(1/x)−1)/(x+(1/x)+1)))∣_(−∞) ^∞ ] =(1/2)[(1/(√3))((Π/2)+(Π/2))−(1/(2 )){ln(((∞−1)/(∞+1)))−ln∣(((−∞−1)/(−∞+2)))∣] (1/2)[(Π/(√3))−(1/2){ln(((1−0)/(1+0)))−ln∣(((∞+1)/(2−∞)))∣}] (1/2)[(Π/(√3))−(1/2){0−ln∣((1+(1/∞))/((2/∞)−1))∣}] (1/2)×(Π/(√3))−(1/2)(0−0) (Π/(2(√3)))](Q42572.png)
| ||
Question and Answers Forum | ||
Question Number 42503 by maxmathsup by imad last updated on 26/Aug/18 | ||
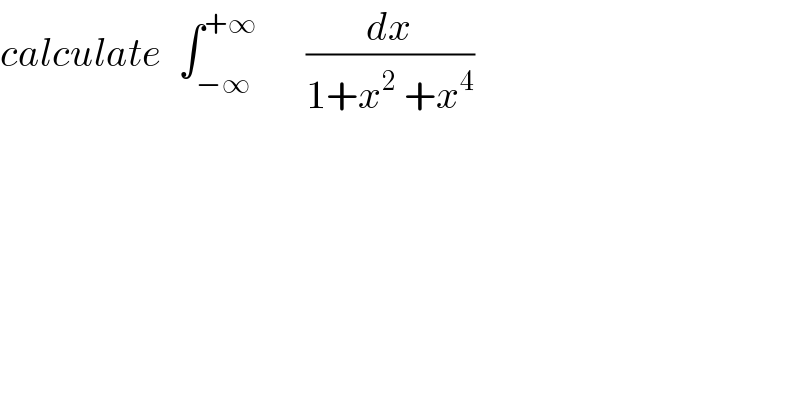 | ||
Commented by maxmathsup by imad last updated on 27/Aug/18 | ||
 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18 | ||
![∫_(−∞) ^∞ ((1/x^2 )/(x^2 +(1/x^2 )+1))dx (1/2)∫_(−∞) ^∞ ((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )+1))dx (1/2)[∫_(−∞) ^∞ ((d(x−(1/x)))/((x−(1/x))^2 +3))−∫_(−∞) ^∞ ((d(x+(1/x)))/((x+(1/x))^2 −1))] (1/2)[∣(1/(√3))tan^(−1) (((x−(1/x))/(√3)))∣_(−∞) ^∞ −(1/(2×1))∣ln(((x+(1/x)−1)/(x+(1/x)+1)))∣_(−∞) ^∞ ] =(1/2)[(1/(√3))((Π/2)+(Π/2))−(1/(2 )){ln(((∞−1)/(∞+1)))−ln∣(((−∞−1)/(−∞+2)))∣] (1/2)[(Π/(√3))−(1/2){ln(((1−0)/(1+0)))−ln∣(((∞+1)/(2−∞)))∣}] (1/2)[(Π/(√3))−(1/2){0−ln∣((1+(1/∞))/((2/∞)−1))∣}] (1/2)×(Π/(√3))−(1/2)(0−0) (Π/(2(√3)))](Q42572.png) | ||
| ||