let f(x)=2(√(x−1)) −2x 1) find D_f 2) study the variation of f(x) 3 ) calculate ∫_1 ^3 f(x)dx 4) determine f^(−1) (x) and calculate ∫_1 ^3 f^(−1) (x)dx 5) find the values of A = ∫_1 ^3 ((f(x))/(f^(−1) (x)dx)) and B = ((∫_1 ^3 f(x))/(∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 42631 by maxmathsup by imad last updated on 29/Aug/18

$l e t f (x) = 2 \sqrt{x - 1} - 2 x$ $1) f i n d D_{f}$ $2) s t u d y t h e v a r i a t i o n o f f (x)$ $3) c a l c u l a t e \int_{1}^{3} f (x) d x$ $4) d e t e r m i n e f^{- 1} (x) a n d c a l c u l a t e \int_{1}^{3} f^{- 1} (x) d x$ $5) f i n d t h e v a l u e s o f A = \int_{1}^{3} \frac{f (x)}{f^{- 1} (x) d x} a n d$ $B = \frac{\int_{1}^{3} f (x)}{\int_{1}^{3} f^{- 1} (x)} d x .$
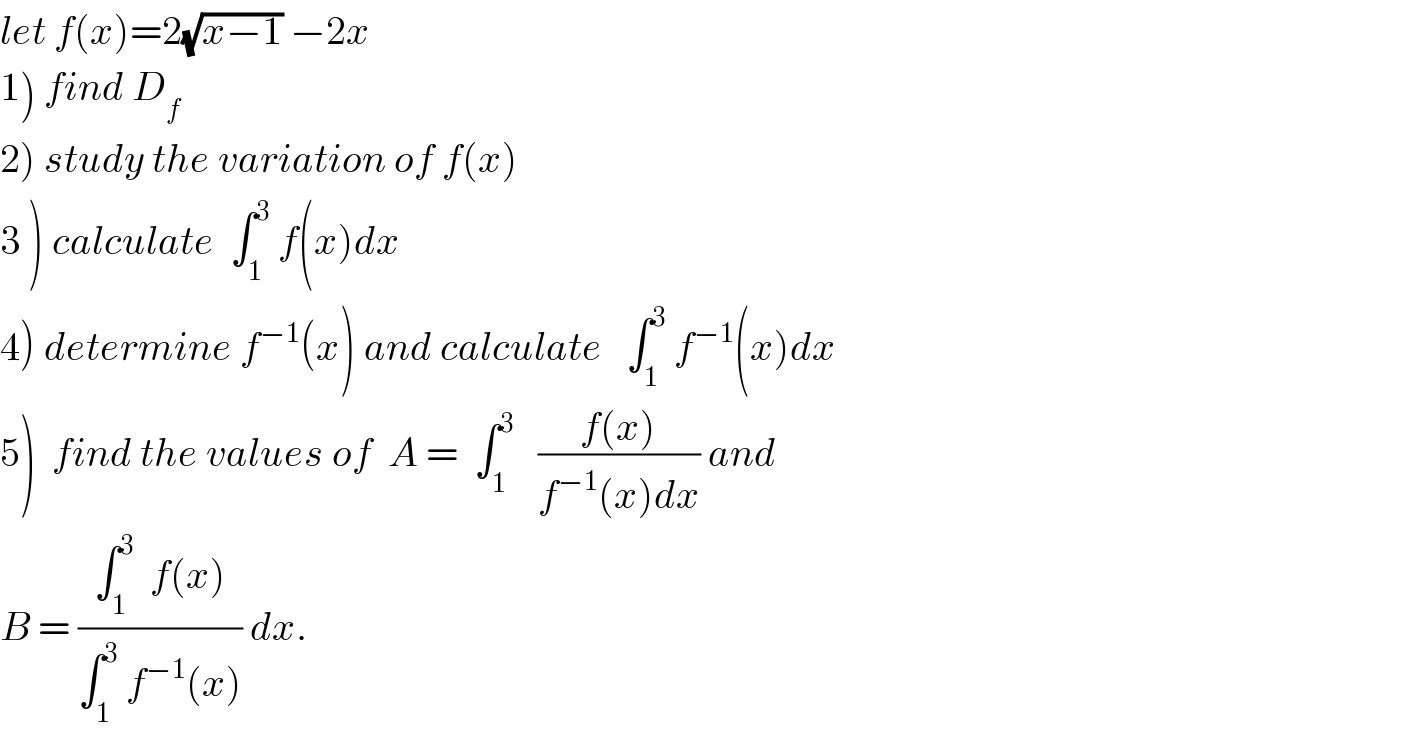
Commented by bbnnftm833 last updated on 30/Aug/18

$w e n e e d t h e s o l u t i o n$
Commented by maxmathsup by imad last updated on 31/Aug/18

$1) x \in D_{f} \Leftrightarrow x - 1 ⩾ 0 \Rightarrow D_{f} = [1, + \infty [$ $2) {l i m}_{x \to + \infty} f (x) = {l i m}_{x \to + \infty} 2 x (\sqrt{\frac{x - 1}{x^{2}}} - 1) = {l i m}_{x \to + \infty} 2 x (\sqrt{\frac{1}{x} - \frac{1}{x^{2}}} - 1)$ $= {l i m}_{x \to + \infty} - 2 x = - \infty$ $w e h a v e f^{^{'}} (x) = \frac{1}{\sqrt{x - 1}} - 2 f o r x > 1 \Rightarrow f^{^{'}} (x) = \frac{1 - 2 \sqrt{x - 1}}{\sqrt{x - 1}}$ $f^{^{'}} (x) = 0 \Leftrightarrow 2 \sqrt{x - 1} = 1 \Leftrightarrow \sqrt{x - 1} = \frac{1}{2} \Leftrightarrow x - 1 = \frac{1}{4} \Leftrightarrow x = \frac{5}{4}$ $f^{^{'}} (x) > 0 \Leftrightarrow 1 - 2 \sqrt{x - 1} > 0 \Leftrightarrow 2 \sqrt{x - 1} < 1 \Leftrightarrow 1 < x < \frac{5}{4}$ $f^{^{'}} (x) < 0 \Leftrightarrow x > \frac{5}{4}$ $x_{} 1 \frac{5}{4} + \infty$ $f^{^{'}} (x) + -$ $f (x) - 2 i n c - \frac{3}{2} d e c r f (1) = - 2 f (\frac{5}{4}) = 2 \sqrt{\frac{5}{4} - 1} - 2 \frac{5}{4}$ $= 1 - \frac{5}{2} = - \frac{3}{2}$
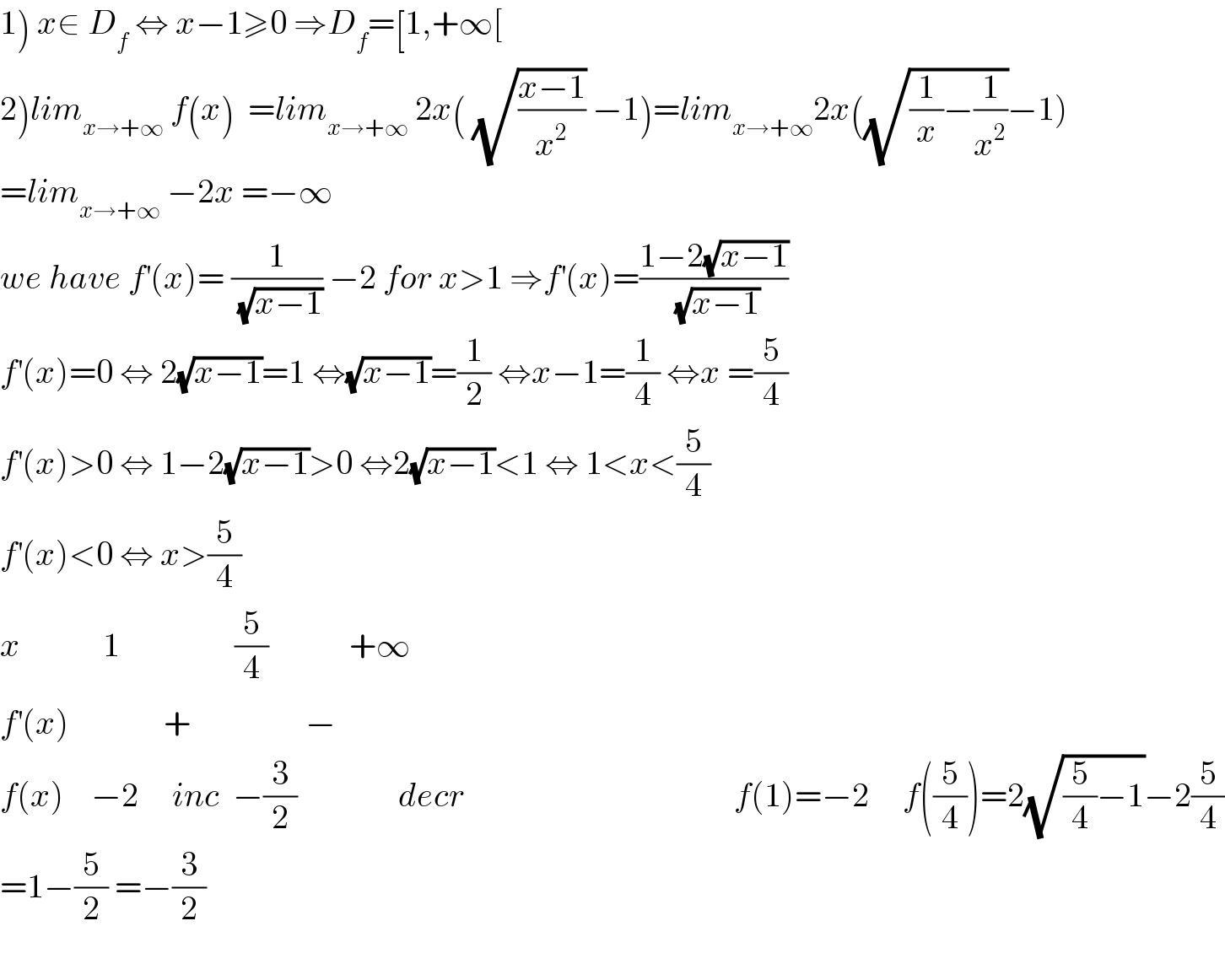
Commented by maxmathsup by imad last updated on 31/Aug/18
$3) ∫_1 ^3 f(x)dx = ∫_1 ^3 {2(√(x−1))−2x}dx = 2 [(2/3)(x−1)^(3/2) ]_1 ^3 − [x^2 ]_1 ^3 =(4/3){ 2^(3/2) } −(9−1) = (4/3)(√2^3 ) −8 =(4/3)(2(√2)) −8 =((8(√2))/3) −8 .$
$3) \int_{1}^{3} f (x) d x = \int_{1}^{3} {2 \sqrt{x - 1} - 2 x} d x = 2 {[\frac{2}{3} {(x - 1)}^{\frac{3}{2}}]}_{1}^{3} - {[x^{2}]}_{1}^{3}$ $= \frac{4}{3} {2^{\frac{3}{2}}} - (9 - 1) = \frac{4}{3} \sqrt{2^{3}} - 8 = \frac{4}{3} (2 \sqrt{2}) - 8 = \frac{8 \sqrt{2}}{3} - 8 .$
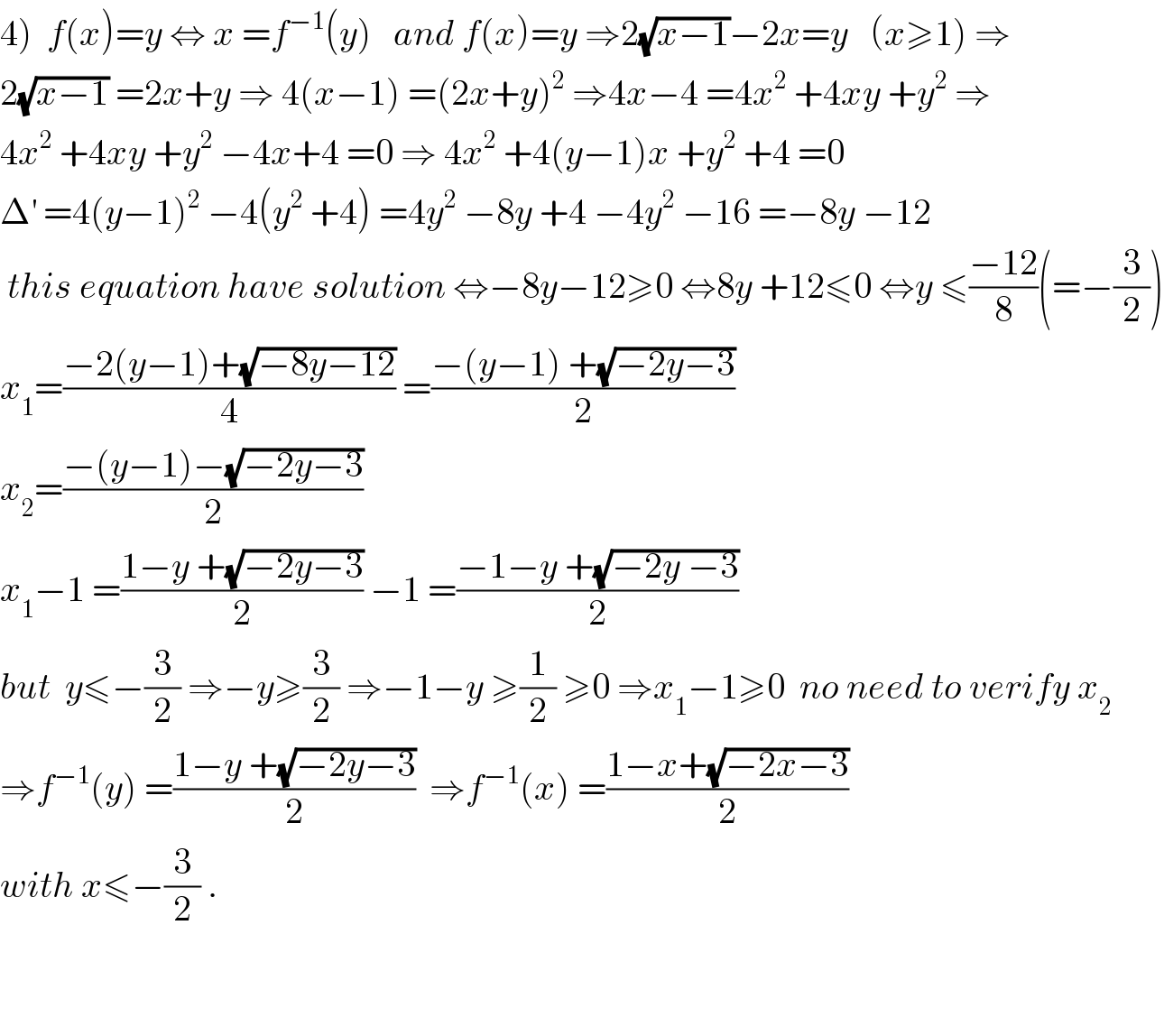
Commented by maxmathsup by imad last updated on 31/Aug/18

$4) f (x) = y \Leftrightarrow x = f^{- 1} (y) a n d f (x) = y \Rightarrow 2 \sqrt{x - 1} - 2 x = y (x ⩾ 1) \Rightarrow$ $2 \sqrt{x - 1} = 2 x + y \Rightarrow 4 (x - 1) = {(2 x + y)}^{2} \Rightarrow 4 x - 4 = 4 x^{2} + 4 x y + y^{2} \Rightarrow$ $4 x^{2} + 4 x y + y^{2} - 4 x + 4 = 0 \Rightarrow 4 x^{2} + 4 (y - 1) x + y^{2} + 4 = 0$ $Δ^{^{'}} = 4 {(y - 1)}^{2} - 4 (y^{2} + 4) = 4 y^{2} - 8 y + 4 - 4 y^{2} - 16 = - 8 y - 12$ $t h i s e q u a t i o n h a v e s o l u t i o n \Leftrightarrow - 8 y - 12 ⩾ 0 \Leftrightarrow 8 y + 12 ⩽ 0 \Leftrightarrow y ⩽ \frac{- 12}{8} (= - \frac{3}{2})$ $x_{1} = \frac{- 2 (y - 1) + \sqrt{- 8 y - 12}}{4} = \frac{- (y - 1) + \sqrt{- 2 y - 3}}{2}$ $x_{2} = \frac{- (y - 1) - \sqrt{- 2 y - 3}}{2}$ $x_{1} - 1 = \frac{1 - y + \sqrt{- 2 y - 3}}{2} - 1 = \frac{- 1 - y + \sqrt{- 2 y - 3}}{2}$ $b u t y ⩽ - \frac{3}{2} \Rightarrow - y ⩾ \frac{3}{2} \Rightarrow - 1 - y ⩾ \frac{1}{2} ⩾ 0 \Rightarrow x_{1} - 1 ⩾ 0 n o n e e d t o v e r i f y x_{2}$ $\Rightarrow f^{- 1} (y) = \frac{1 - y + \sqrt{- 2 y - 3}}{2} \Rightarrow f^{- 1} (x) = \frac{1 - x + \sqrt{- 2 x - 3}}{2}$ $w i t h x ⩽ - \frac{3}{2} .$
Commented by maxmathsup by imad last updated on 31/Aug/18

$4) f o r g i v e t h e Q i s c a l c u l a t e \int_{- 3}^{- 2} f^{- 1} (x) d x$ $5) t h e Q i s f i n d t h e v a l u e o f A = \frac{\int_{2}^{3} f (x) d x}{\int_{- 3}^{- 2} f^{- 1} (x) d x}$ $B = \int \frac{f (x)}{f^{- 1} (x)} d x .$
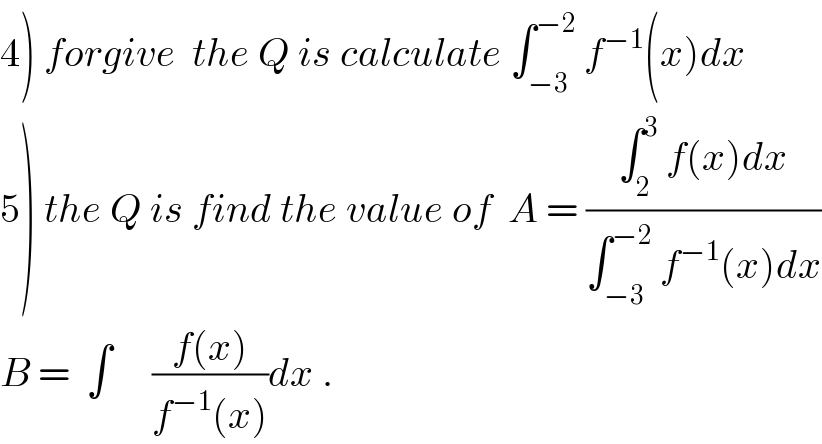
Commented by maxmathsup by imad last updated on 31/Aug/18
$4) we have f^(−1) (x)=((1−x+(√(−2x−3)))/2) ⇒ ∫_(−3) ^(−2) f^(−1) (x)dx =(1/2) ∫_(−3) ^(−2) (1−x) +(1/2) ∫_(−3) ^(−2) (√(−2x−3))dx but ∫_(−3) ^(−2) (1−x)dx =[x−(x^2 /2)]_(−3) ^(−2) =−2−2−(−3−(9/2))=−1 +(9/2) =(7/2) and ∫_(−3) ^(−2) (√(−2x−3))dx =[−(1/3)(−2x−3)^(3/2) ]_(−3) ^(−2) =−(1/3){1−(3)^(3/2) } =(√3) −(1/3) ⇒∫_(−3) ^(−2) f^(−1) (x)dx = (7/4) +((√3)/2) −(1/6) =((38)/(24)) +((√3)/2) =((19)/(12)) +((√3)/2)$
$4) w e h a v e f^{- 1} (x) = \frac{1 - x + \sqrt{- 2 x - 3}}{2} \Rightarrow$ $\int_{- 3}^{- 2} f^{- 1} (x) d x = \frac{1}{2} \int_{- 3}^{- 2} (1 - x) + \frac{1}{2} \int_{- 3}^{- 2} \sqrt{- 2 x - 3} d x b u t$ $\int_{- 3}^{- 2} (1 - x) d x = {[x - \frac{x^{2}}{2}]}_{- 3}^{- 2} = - 2 - 2 - (- 3 - \frac{9}{2}) = - 1 + \frac{9}{2} = \frac{7}{2} a n d$ $\int_{- 3}^{- 2} \sqrt{- 2 x - 3} d x = {[- \frac{1}{3} {(- 2 x - 3)}^{\frac{3}{2}}]}_{- 3}^{- 2} = - \frac{1}{3} {1 - {(3)}^{\frac{3}{2}}}$ $= \sqrt{3} - \frac{1}{3} \Rightarrow \int_{- 3}^{- 2} f^{- 1} (x) d x = \frac{7}{4} + \frac{\sqrt{3}}{2} - \frac{1}{6} = \frac{38}{24} + \frac{\sqrt{3}}{2} = \frac{19}{12} + \frac{\sqrt{3}}{2}$
Commented by maxmathsup by imad last updated on 31/Aug/18
$5) we have ∫_2 ^3 f(x)dx = 2 ∫_2 ^3 (√(x−1)) −∫_2 ^3 2x dx =2[(2/3)(x−1)^(3/2) ]_2 ^3 −[x^2 ]_2 ^3 =(4/3){ 2^(3/2) −1}−{9−4} =(4/3)(2(√2)) −5 =((8(√2))/3) −5 also we have ∫_(−3) ^(−2) f^(−1) (x)dx =((19)/(12)) +((√3)/2) ⇒ A = ((∫_2 ^3 f(x)dx)/(∫_(−3) ^(−2) f^(−1) (x)dx)) = ((((8(√2))/3)−5)/(((19)/(12)) +((√3)/2))) .$
$5) w e h a v e \int_{2}^{3} f (x) d x = 2 \int_{2}^{3} \sqrt{x - 1} - \int_{2}^{3} 2 x d x$ $= 2 {[\frac{2}{3} {(x - 1)}^{\frac{3}{2}}]}_{2}^{3} - {[x^{2}]}_{2}^{3} = \frac{4}{3} {2^{\frac{3}{2}} - 1} - {9 - 4}$ $= \frac{4}{3} (2 \sqrt{2}) - 5 = \frac{8 \sqrt{2}}{3} - 5 a l s o w e h a v e \int_{- 3}^{- 2} f^{- 1} (x) d x = \frac{19}{12} + \frac{\sqrt{3}}{2} \Rightarrow$ $A = \frac{\int_{2}^{3} f (x) d x}{\int_{- 3}^{- 2} f^{- 1} (x) d x} = \frac{\frac{8 \sqrt{2}}{3} - 5}{\frac{19}{12} + \frac{\sqrt{3}}{2}} .$
	Answered by behi83417@gmail.com last updated on 30/Aug/18

	$1) x - 1 ⩾ 0 \Rightarrow x ⩾ 1 \Rightarrow D_{f} = [1, + \infty)$ $2) y = 2 \sqrt{x - 1} - 2 x$ $y^{'} = \frac{1}{\sqrt{x - 1}} - 2 \Rightarrow x \neq 1 \Rightarrow D_{f} = (1, + \infty)$ $x - 1 = t^{2} \Rightarrow x = t^{2} + 1$ $f (t) = 2 t - 2 (t^{2} + 1) = - 2 (t^{2} - t + 1)$ $\Rightarrow t^{2} - t + 1 = \frac{- y}{2} \Rightarrow {(t - \frac{1}{2})}^{2} = \frac{- y}{2} - \frac{3}{4}$ $\Rightarrow t - \frac{1}{2} = \pm \sqrt{- \frac{2 y + 3}{4}} \Rightarrow t = \frac{1}{2} (1 \pm \sqrt{- 2 y - 3})$ $\Rightarrow \sqrt{x - 1} = \frac{1}{2} (1 \pm \sqrt{- 2 y - 3})$ $\Rightarrow x = 1 + \frac{1}{4} {(1 \pm \sqrt{- 2 y - 3})}^{2}$ $\Rightarrow f^{- 1} (x) = 1 + \frac{1}{4} {(1 \pm \sqrt{- 2 x - 3})}^{2}$ $- 2 y - 3 ⩾ 0 \Rightarrow 2 y + 3 ⩽ 0 \Rightarrow y ⩽ - \frac{3}{2}$ $\Rightarrow R_{f} = (- \infty, - \frac{3}{2}] .$ $3) \underset{1}{\int^{3}} f (x) d x = \underset{1}{\int^{3}} (2 \sqrt{x - 1} - 2 x) d x =$ $Missing \left or extra \right$ $4) \int f^{- 1} (x) d x = \int [1 + \frac{1}{4} {(1 \pm \sqrt{- 2 x - 3})}^{2}] d x =$ $= \int [1 + \frac{1}{4} (1 \mp (2 x + 3) \pm 2 \sqrt{- 2 x - 3})] d x$ $I_{1} = \int [1 + \frac{1}{4} (2 x + 4 + 2 \sqrt{- 2 x - 3})] d x =$ $Missing \left or extra \right$ $= \frac{1}{2} [6 + 8 - 27 i - 2 - 2 + \frac{i \sqrt{5}}{3}] =$ $= 5 - \frac{81 - \sqrt{5}}{6} . i$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum