Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4266 by Rasheed Soomro last updated on 06/Jan/16

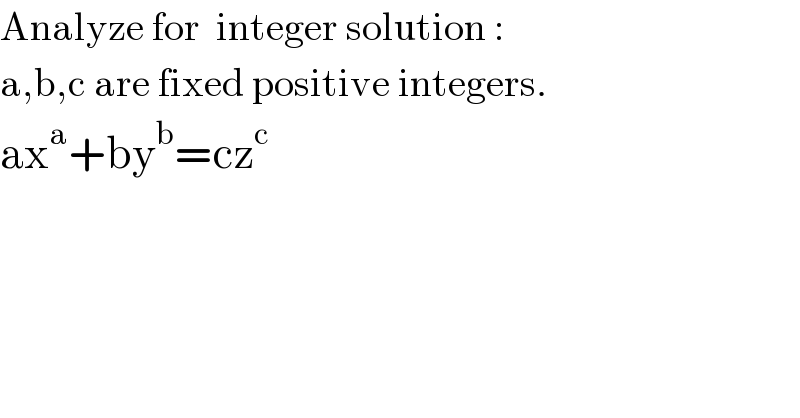
Analyze for integer solution : a,b,c are fixed positive integers. ax^a +by^b =cz^c

$$\mathrm{Analyze}\:\mathrm{for}\:\:\mathrm{integer}\:\mathrm{solution}\:: \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are}\:\mathrm{fixed}\:\mathrm{positive}\:\mathrm{integers}. \\ $$$$\mathrm{ax}^{\mathrm{a}} +\mathrm{by}^{\mathrm{b}} =\mathrm{cz}^{\mathrm{c}} \\ $$

Commented by Yozzii last updated on 06/Jan/16

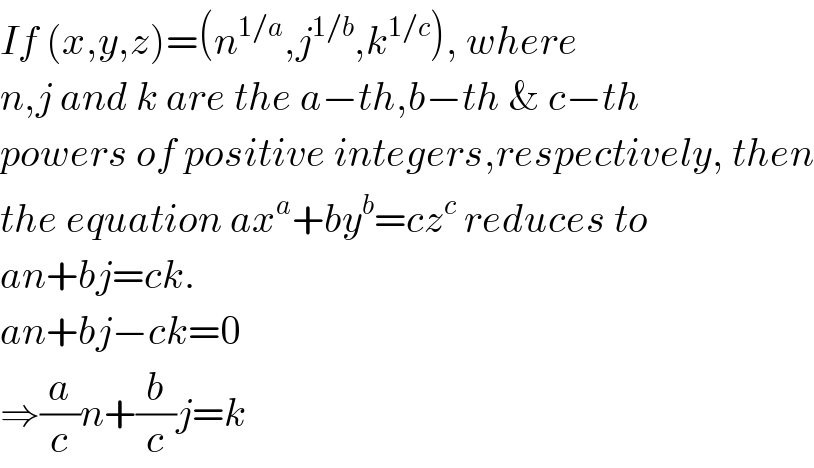
If (x,y,z)=(n^(1/a) ,j^(1/b) ,k^(1/c) ), where n,j and k are the a−th,b−th & c−th powers of positive integers,respectively, then the equation ax^a +by^b =cz^c reduces to an+bj=ck. an+bj−ck=0 ⇒(a/c)n+(b/c)j=k

$${If}\:\left({x},{y},{z}\right)=\left({n}^{\mathrm{1}/{a}} ,{j}^{\mathrm{1}/{b}} ,{k}^{\mathrm{1}/{c}} \right),\:{where} \\ $$$${n},{j}\:{and}\:{k}\:{are}\:{the}\:{a}−{th},{b}−{th}\:\&\:{c}−{th} \\ $$$${powers}\:{of}\:{positive}\:{integers},{respectively},\:{then} \\ $$$${the}\:{equation}\:{ax}^{{a}} +{by}^{{b}} ={cz}^{{c}} \:{reduces}\:{to}\:\: \\ $$$${an}+{bj}={ck}. \\ $$$${an}+{bj}−{ck}=\mathrm{0}\: \\ $$$$\Rightarrow\frac{{a}}{{c}}{n}+\frac{{b}}{{c}}{j}={k} \\ $$

Commented by prakash jain last updated on 06/Jan/16

a=b=c=1 x+y=z a=b=c=2 pythogorean triples a=b=c≥3 no solution

$${a}={b}={c}=\mathrm{1} \\ $$$${x}+{y}={z} \\ $$$${a}={b}={c}=\mathrm{2} \\ $$$${pythogorean}\:{triples} \\ $$$${a}={b}={c}\geqslant\mathrm{3}\:\mathrm{no}\:\mathrm{solution} \\ $$

Commented by Rasheed Soomro last updated on 13/Jan/16

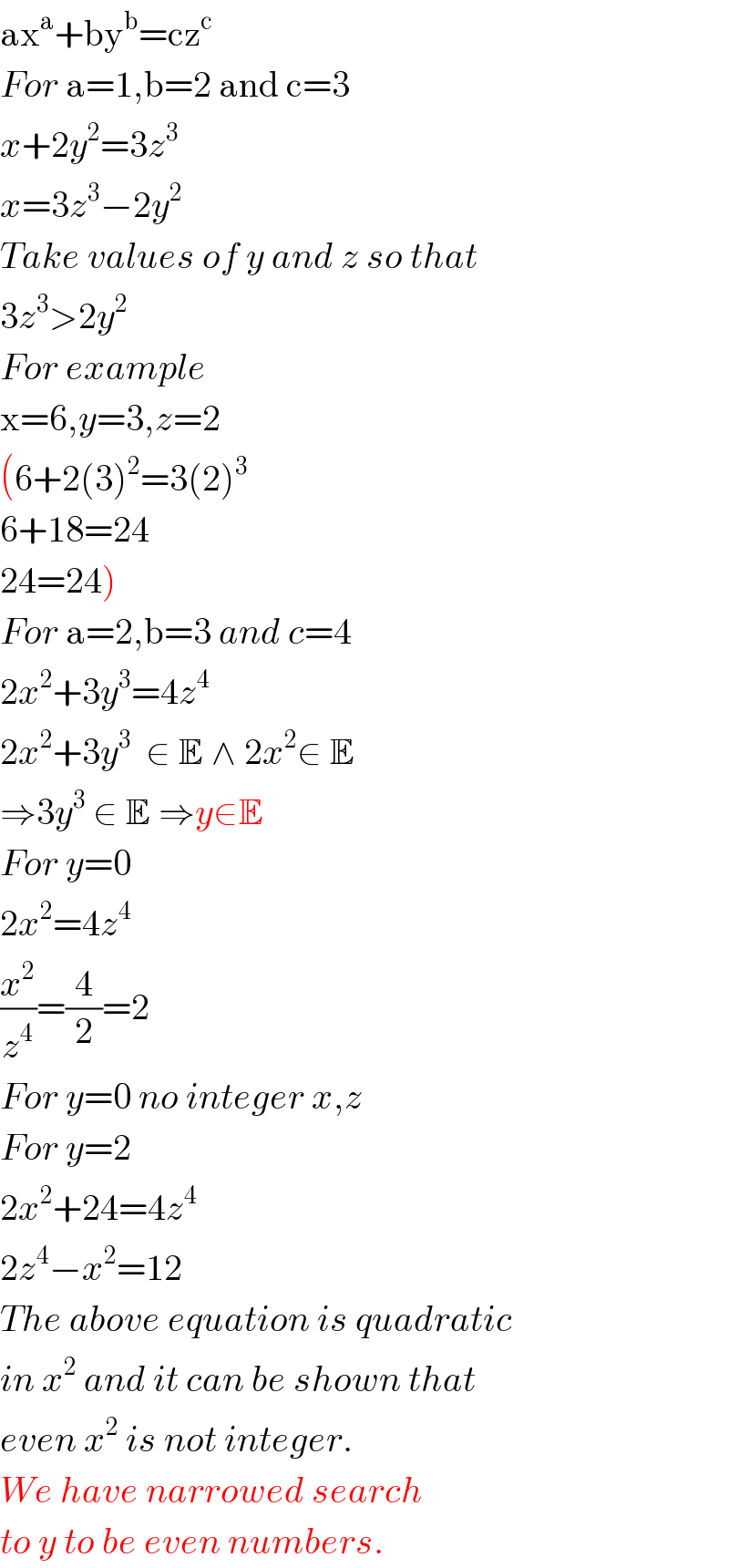
ax^a +by^b =cz^c For a=1,b=2 and c=3 x+2y^2 =3z^3 x=3z^3 −2y^2 Take values of y and z so that 3z^3 >2y^2 For example x=6,y=3,z=2 (6+2(3)^2 =3(2)^3 6+18=24 24=24) For a=2,b=3 and c=4 2x^2 +3y^3 =4z^4 2x^2 +3y^3 ∈ E ∧ 2x^2 ∈ E ⇒3y^3 ∈ E ⇒y∈E For y=0 2x^2 =4z^4 (x^2 /z^4 )=(4/2)=2 For y=0 no integer x,z For y=2 2x^2 +24=4z^4 2z^4 −x^2 =12 The above equation is quadratic in x^2 and it can be shown that even x^2 is not integer. We have narrowed search to y to be even numbers.

$$\mathrm{ax}^{\mathrm{a}} +\mathrm{by}^{\mathrm{b}} =\mathrm{cz}^{\mathrm{c}} \\ $$$${For}\:\mathrm{a}=\mathrm{1},\mathrm{b}=\mathrm{2}\:\mathrm{and}\:\mathrm{c}=\mathrm{3} \\ $$$${x}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{3}{z}^{\mathrm{3}} \\ $$$${x}=\mathrm{3}{z}^{\mathrm{3}} −\mathrm{2}{y}^{\mathrm{2}} \\ $$$${Take}\:{values}\:{of}\:{y}\:{and}\:{z}\:{so}\:{that} \\ $$$$\mathrm{3}{z}^{\mathrm{3}} >\mathrm{2}{y}^{\mathrm{2}} \\ $$$${For}\:{example} \\ $$$$\mathrm{x}=\mathrm{6},{y}=\mathrm{3},{z}=\mathrm{2} \\ $$$$\left(\mathrm{6}+\mathrm{2}\left(\mathrm{3}\right)^{\mathrm{2}} =\mathrm{3}\left(\mathrm{2}\right)^{\mathrm{3}} \right. \\ $$$$\mathrm{6}+\mathrm{18}=\mathrm{24} \\ $$$$\left.\mathrm{24}=\mathrm{24}\right) \\ $$$${For}\:\mathrm{a}=\mathrm{2},\mathrm{b}=\mathrm{3}\:{and}\:{c}=\mathrm{4} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{3}} =\mathrm{4}{z}^{\mathrm{4}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{3}} \:\:\in\:\mathbb{E}\:\wedge\:\mathrm{2}{x}^{\mathrm{2}} \in\:\mathbb{E} \\ $$$$\Rightarrow\mathrm{3}{y}^{\mathrm{3}} \:\in\:\mathbb{E}\:\Rightarrow{y}\in\mathbb{E} \\ $$$${For}\:{y}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} =\mathrm{4}{z}^{\mathrm{4}} \\ $$$$\frac{{x}^{\mathrm{2}} }{{z}^{\mathrm{4}} }=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$$${For}\:{y}=\mathrm{0}\:{no}\:{integer}\:{x},{z} \\ $$$${For}\:{y}=\mathrm{2} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{24}=\mathrm{4}{z}^{\mathrm{4}} \\ $$$$\mathrm{2}{z}^{\mathrm{4}} −{x}^{\mathrm{2}} =\mathrm{12} \\ $$$${The}\:{above}\:{equation}\:{is}\:{quadratic}\: \\ $$$${in}\:{x}^{\mathrm{2}} \:{and}\:{it}\:{can}\:{be}\:{shown}\:{that} \\ $$$${even}\:{x}^{\mathrm{2}} \:{is}\:{not}\:{integer}. \\ $$$${We}\:{have}\:{narrowed}\:{search} \\ $$$${to}\:{y}\:{to}\:{be}\:{even}\:{numbers}. \\ $$

Answered by Rasheed Soomro last updated on 11/Jan/16

ax^a +by^b =cz^c Let a=4j^2 , b=4k^2 , c=4l^2 4j^2 x^(4j^2 ) +4k^2 y^(4k^2 ) =4l^2 z^(4l^2 ) j^2 x^(4j^2 ) +k^2 y^(4k^2 ) =l^2 z^(4l^2 ) (jx^(2j^2 ) )^2 +(ky^(2k^2 ) )^2 =(lz^(2l^2 ) )^2 (jx^(2j^2 ) ,ky^(2k^2 ) ,lz^(2l^2 ) ) is Pythagorean triple. −−−−−−−−−−− If (X,Y,Z) is Pythagorean triplet such that j∣X ,k∣Y and l∣Z ((1/j) X^( (1/(2j^2 ))) , (1/k)Y^( (1/(2k^2 ))) , (1/l)Z^( (1/(2l^2 ))) ) is triplet satisfying ax^a +by^b =cz^c where j=((√a)/2) ,k=((√b)/2) ,l=((√c)/2) a,b,c perfect squares and even −−−−−−−−OR−−−−−−− If (X,Y,Z) is Pythagorean triplet such that ((√a)/2) ∣ X ,((√b)/2) ∣ Y and ((√c)/2) ∣Z Also X^(1/a) ,Y^(1/b) ,Z^(1/c) are integers. ((2/(√a)) X^(2/a) , (2/(√b)) Y^(2/b) ,(2/(√c)) Z^(2/c) ) is a required triple . a,b,c are perfect squares and even. j=1,k=2,l=3 (x^2 )^2 +(2y^8 )^2 =(3z^(18) )^2 x^4 +4y^(16) =9z^(36) −−−−−− (m^2 −n^2 ,2mn,m^2 +n^2 ) is general triple,suggested by Euclid ∀ m,n∈N ∧ m>n −−−−−−−−−− For 2mn to be of bx^b type let m=(b/2)n^(b−1) 2mn=bn^b m^2 +n^2 =(bn^b )^2 +n^2 =b^2 n^(2b) +n^2 =(b^2 n^(2b−2) +1)n^2 =cn^c (b^2 n^(2b−2) +1)=cn^(c−2) Continue

$$\mathrm{ax}^{\mathrm{a}} +\mathrm{by}^{\mathrm{b}} =\mathrm{cz}^{\mathrm{c}} \\ $$$${Let}\:\mathrm{a}=\mathrm{4j}^{\mathrm{2}} \:,\:\mathrm{b}=\mathrm{4k}^{\mathrm{2}} \:,\:\mathrm{c}=\mathrm{4}{l}^{\mathrm{2}} \\ $$$$\mathrm{4j}^{\mathrm{2}} \mathrm{x}^{\mathrm{4j}^{\mathrm{2}} } +\mathrm{4k}^{\mathrm{2}} \mathrm{y}^{\mathrm{4k}^{\mathrm{2}} } =\mathrm{4}{l}^{\mathrm{2}} \mathrm{z}^{\mathrm{4}{l}^{\mathrm{2}} } \\ $$$$\mathrm{j}^{\mathrm{2}} \mathrm{x}^{\mathrm{4j}^{\mathrm{2}} } +\mathrm{k}^{\mathrm{2}} \mathrm{y}^{\mathrm{4k}^{\mathrm{2}} } ={l}^{\mathrm{2}} \mathrm{z}^{\mathrm{4}{l}^{\mathrm{2}} } \\ $$$$\left(\mathrm{jx}^{\mathrm{2j}^{\mathrm{2}} } \right)^{\mathrm{2}} +\left(\mathrm{ky}^{\mathrm{2k}^{\mathrm{2}} } \right)^{\mathrm{2}} =\left({l}\mathrm{z}^{\mathrm{2}{l}^{\mathrm{2}} } \right)^{\mathrm{2}} \\ $$$$\left(\mathrm{jx}^{\mathrm{2j}^{\mathrm{2}} } ,\mathrm{ky}^{\mathrm{2k}^{\mathrm{2}} } ,{l}\mathrm{z}^{\mathrm{2}{l}^{\mathrm{2}} } \right)\:{is}\:{Pythagorean}\:{triple}. \\ $$$$−−−−−−−−−−− \\ $$$$\mathrm{If}\:\left(\mathrm{X},\mathrm{Y},\mathrm{Z}\right)\:{is}\:{Pythagorean}\:{triplet} \\ $$$${such}\:{that}\:\mathrm{j}\mid\mathrm{X}\:,\mathrm{k}\mid\mathrm{Y}\:{and}\:{l}\mid\mathrm{Z} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{j}}\:\mathrm{X}^{\:\frac{\mathrm{1}}{\mathrm{2j}^{\mathrm{2}} }} \:,\:\frac{\mathrm{1}}{{k}}\mathrm{Y}^{\:\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }} \:,\:\frac{\mathrm{1}}{{l}}\mathrm{Z}^{\:\frac{\mathrm{1}}{\mathrm{2}{l}^{\mathrm{2}} }} \:\right)\:{is}\:{triplet} \\ $$$${satisfying}\:\:\mathrm{ax}^{\mathrm{a}} +\mathrm{by}^{\mathrm{b}} =\mathrm{cz}^{\mathrm{c}} \:{where} \\ $$$${j}=\frac{\sqrt{\mathrm{a}}}{\mathrm{2}}\:,{k}=\frac{\sqrt{\mathrm{b}}}{\mathrm{2}}\:,{l}=\frac{\sqrt{\mathrm{c}}}{\mathrm{2}} \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{perfect}\:\mathrm{squares}\:\mathrm{and}\:\mathrm{even} \\ $$$$−−−−−−−−\mathcal{OR}−−−−−−− \\ $$$$\mathrm{If}\:\left(\mathrm{X},\mathrm{Y},\mathrm{Z}\right)\:{is}\:{Pythagorean}\:{triplet} \\ $$$${such}\:{that}\:\frac{\sqrt{\mathrm{a}}}{\mathrm{2}}\:\mid\:\mathrm{X}\:,\frac{\sqrt{\mathrm{b}}}{\mathrm{2}}\:\mid\:\mathrm{Y}\:\mathrm{and}\:\frac{\sqrt{\mathrm{c}}}{\mathrm{2}}\:\mid{Z} \\ $$$$\mathrm{Also}\:\:\mathrm{X}^{\frac{\mathrm{1}}{\mathrm{a}}} \:,\mathrm{Y}^{\frac{\mathrm{1}}{\mathrm{b}}} ,\mathrm{Z}^{\frac{\mathrm{1}}{\mathrm{c}}} \:\mathrm{are}\:\mathrm{integers}. \\ $$$$\:\left(\frac{\mathrm{2}}{\sqrt{\mathrm{a}}}\:\mathrm{X}^{\frac{\mathrm{2}}{\mathrm{a}}} ,\:\frac{\mathrm{2}}{\sqrt{\mathrm{b}}}\:\mathrm{Y}^{\frac{\mathrm{2}}{\mathrm{b}}} ,\frac{\mathrm{2}}{\sqrt{\mathrm{c}}}\:\mathrm{Z}^{\frac{\mathrm{2}}{\mathrm{c}}} \right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{required}\:\mathrm{triple}\:. \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are}\:\mathrm{perfect}\:\mathrm{squares}\:\mathrm{and}\:\mathrm{even}. \\ $$$$\mathrm{j}=\mathrm{1},\mathrm{k}=\mathrm{2},{l}=\mathrm{3} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{2y}^{\mathrm{8}} \right)^{\mathrm{2}} =\left(\mathrm{3z}^{\mathrm{18}} \right)^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{4y}^{\mathrm{16}} =\mathrm{9z}^{\mathrm{36}} \\ $$$$−−−−−− \\ $$$$\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} ,\mathrm{2}{mn},{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)\:{is}\:{general} \\ $$$${triple},{suggested}\:{by}\:\mathcal{E}{uclid} \\ $$$$\forall\:{m},{n}\in\mathbb{N}\:\wedge\:{m}>{n} \\ $$$$−−−−−−−−−− \\ $$$$\mathrm{For}\:\mathrm{2mn}\:\mathrm{to}\:\mathrm{be}\:\mathrm{of}\:\mathrm{bx}^{\mathrm{b}} \:\mathrm{type} \\ $$$$\mathrm{let}\:\mathrm{m}=\frac{\mathrm{b}}{\mathrm{2}}\mathrm{n}^{\mathrm{b}−\mathrm{1}} \\ $$$$\mathrm{2mn}=\mathrm{bn}^{\mathrm{b}} \\ $$$$\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} =\left(\mathrm{bn}^{\mathrm{b}} \right)^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \mathrm{n}^{\mathrm{2b}} +\mathrm{n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{b}^{\mathrm{2}} \mathrm{n}^{\mathrm{2b}−\mathrm{2}} +\mathrm{1}\right)\mathrm{n}^{\mathrm{2}} =\mathrm{cn}^{\mathrm{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{b}^{\mathrm{2}} \mathrm{n}^{\mathrm{2b}−\mathrm{2}} +\mathrm{1}\right)=\mathrm{cn}^{\mathrm{c}−\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Continue} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com