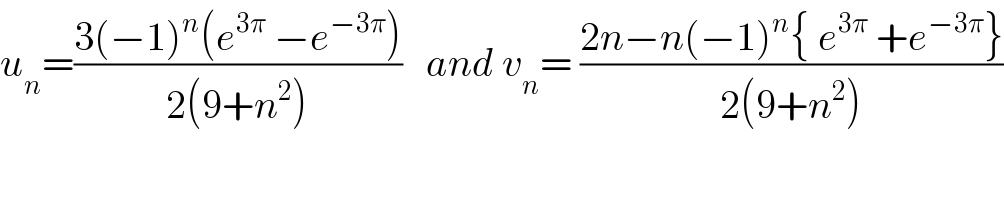Question Number 42704 by maxmathsup by imad last updated on 01/Sep/18
![f(x) = ((e^(3x) +e^(−3x) )/2) 1) determine f^(−1) (x) 2) calculate ∫_0 ^1 x f(x)dx and ∫_0 ^1 f(x)dx 3) calculate ∫ f^(−1) (x)dx 4) calculate u_n = ∫_0 ^π f(x)cos(nx)dx and v_n = ∫_0 ^n f(x)sin(nx)dx find nature of Σ (v_n /u_n ) ∫_0 ^1 xf(x) dx =(1/2) ∫_0 ^1 x e^(3x) dx +(1/2) ∫_0 ^1 x e^(−3x) dx (by parts) =(1/2){ [(x/3)e^(3x) ]_0 ^1 −(1/3)∫_0 ^1 e^(3x) dx +[−(x/3)e^(−3x) ]_0 ^1 +(1/3)∫_0 ^1 e^(−3x) dx} =(1/2){(e^3 /3) −(1/9)(e^3 −1) −(e^(−3) /3) −(1/9)(e^(−3) −1)}](Q42704.png)
$${f}\left({x}\right)\:\:=\:\:\frac{{e}^{\mathrm{3}{x}} \:+{e}^{−\mathrm{3}{x}} }{\mathrm{2}} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{x}\:{f}\left({x}\right){dx}\:\:\:\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\left.\mathrm{3}\right)\:\:{calculate}\:\:\:\int\:\:{f}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:{u}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:\:{f}\left({x}\right){cos}\left({nx}\right){dx}\:{and}\:{v}_{{n}} =\:\int_{\mathrm{0}} ^{{n}} \:\:{f}\left({x}\right){sin}\left({nx}\right){dx} \\ $$$${find}\:{nature}\:{of}\:\Sigma\:\frac{{v}_{{n}} }{{u}_{{n}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{xf}\left({x}\right)\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{\mathrm{3}{x}} {dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{−\mathrm{3}{x}} {dx}\:\:\:\left({by}\:{parts}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\left[\frac{{x}}{\mathrm{3}}{e}^{\mathrm{3}{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{\mathrm{3}{x}} {dx}\:\:+\left[−\frac{{x}}{\mathrm{3}}{e}^{−\mathrm{3}{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{−\mathrm{3}{x}} {dx}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{e}^{\mathrm{3}} }{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{9}}\left({e}^{\mathrm{3}} −\mathrm{1}\right)\:−\frac{{e}^{−\mathrm{3}} }{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{9}}\left({e}^{−\mathrm{3}} −\mathrm{1}\right)\right\} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 01/Sep/18
![1) f(x)=ch(3x) =y ⇔ 3x =argch(y) ⇔x =(1/3)argch(y) =(1/3)ln(y+(√(y^2 −1))) ⇒ f^(−1) (x) =(1/3)ln(y+(√(y^2 −1))) 2)∫_0 ^1 f(x)dx = (1/2)∫_0 ^1 ( e^(3x) +e^(−3x) )dx =(1/2)[(1/3)e^(3x) −(1/3)e^(−3x) ]_0 ^1 =(1/6){e^3 −e^(−3) }](Q42732.png)
$$\left.\mathrm{1}\right)\:{f}\left({x}\right)={ch}\left(\mathrm{3}{x}\right)\:={y}\:\Leftrightarrow\:\mathrm{3}{x}\:={argch}\left({y}\right)\:\Leftrightarrow{x}\:=\frac{\mathrm{1}}{\mathrm{3}}{argch}\left({y}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:{e}^{\mathrm{3}{x}} \:+{e}^{−\mathrm{3}{x}} \right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{{e}^{\mathrm{3}} \:−{e}^{−\mathrm{3}} \right\} \\ $$
Commented by maxmathsup by imad last updated on 01/Sep/18
$$\left.\mathrm{3}\right)\:{let}\:{I}\:\:=\:\int\:\:{f}^{−\mathrm{1}} \left({x}\right){dx}\:\:\:{let}\:\:{f}^{−\mathrm{1}} \left({x}\right)\:={t}\:\Rightarrow\:{x}\:={f}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\:\int\:\:{t}\:{f}^{'} \left({t}\right){dt}\:=\:{tf}\left({t}\right)\:−\int\:\:{f}\left({t}\right){dt}\:\:\:{and}\: \\ $$$$\int\:{f}\left({t}\right){dt}\:=\int\:\:\:\frac{{e}^{\mathrm{3}{t}} \:+{e}^{−\mathrm{3}{t}} }{\mathrm{2}}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{6}}\:{e}^{\mathrm{3}{t}} −\frac{\mathrm{1}}{\mathrm{6}}\:{e}^{−\mathrm{3}{t}} \:\:+{c}\:\Rightarrow \\ $$$${I}\:\:=\:{t}\:{f}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{6}}\:{e}^{\mathrm{3}{t}} \:+\frac{\mathrm{1}}{\mathrm{6}}\:{e}^{−\mathrm{3}{t}} \:\:\:{but}\:{t}\:={f}^{−\mathrm{1}} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$${I}\:\:=\frac{{x}}{\mathrm{3}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:−\frac{\mathrm{1}}{\mathrm{6}}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:\:+\frac{\mathrm{1}}{\mathrm{6}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)}\:+{c}\: \\ $$$$ \\ $$
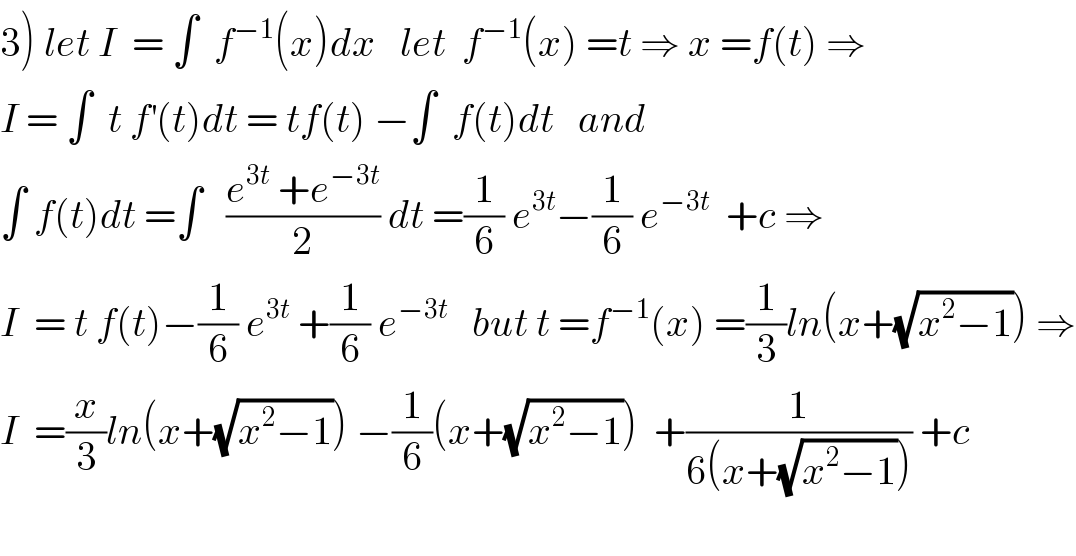
Commented by maxmathsup by imad last updated on 02/Sep/18
![4) we have u_n = ∫_0 ^π f(x)cos(nx)dx =(1/2) ∫_0 ^π (e^(3x) +e^(−3x) )cos(nx)dx ⇒ 2u_n = Re( ∫_0 ^π e^(inx) (e^(3x) +e^(−3x) )dx) =Re( ∫_0 ^π e^((3+in)x) + e^((−3+in)x) )dx but ∫_0 ^π ( e^((3+in)x) +e^((−3+in)x) )dx =[(1/(3+in)) e^((3+in)x) +(1/(−3+in)) e^((−3+in)x) ]_0 ^π =((e^(3π) (−1)^n )/(3+in)) +((e^(−3π) (−1)^n )/(−3 +in)) −(1/(3+in)) −(1/(−3+in)) =(((3−in) e^(3π) (−1)^n )/(9+n^2 )) + (((−3−in)e^(−3π) (−1)^n )/(9+n^2 )) −(1/(3+in)) +(1/(3−in)) =(((−1)^n )/(9+n^2 )) { 3 e^(3π) −in e^(3π) −3 e^(−3π) −in e^(−3π) } +(1/(3−in)) −(1/(3+in)) =((3(−1)^n )/(9+n^2 )){ e^(3π) −e^(−3π) } −((n(−1)^n )/(9+n^2 ))i {e^(3π) +e^(−3π) } +((2in)/(9+n^2 )) ⇒ u_n = ((3(−1)^n (e^(3π) −e^(−3π) ))/(9+n^2 )) also we have v_n = Im(∫_0 ^π e^((3+in)x) +e^((−3+in)x) )dx) ⇒v_n =((2n −n(−1)^n )/(9+n^2 )) .](Q42735.png)
$$\left.\mathrm{4}\right)\:\:{we}\:{have}\:{u}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:{f}\left({x}\right){cos}\left({nx}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\pi} \:\:\left({e}^{\mathrm{3}{x}} \:+{e}^{−\mathrm{3}{x}} \right){cos}\left({nx}\right){dx}\:\Rightarrow \\ $$$$\mathrm{2}{u}_{{n}} =\:{Re}\left(\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{{inx}} \left({e}^{\mathrm{3}{x}} \:+{e}^{−\mathrm{3}{x}} \right){dx}\right)\:={Re}\left(\:\int_{\mathrm{0}} ^{\pi} \:{e}^{\left(\mathrm{3}+{in}\right){x}} \:+\:{e}^{\left(−\mathrm{3}+{in}\right){x}} \right){dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\left(\:{e}^{\left(\mathrm{3}+{in}\right){x}} \:+{e}^{\left(−\mathrm{3}+{in}\right){x}} \right){dx}\:=\left[\frac{\mathrm{1}}{\mathrm{3}+{in}}\:{e}^{\left(\mathrm{3}+{in}\right){x}} \:+\frac{\mathrm{1}}{−\mathrm{3}+{in}}\:{e}^{\left(−\mathrm{3}+{in}\right){x}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{{e}^{\mathrm{3}\pi} \left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}+{in}}\:+\frac{{e}^{−\mathrm{3}\pi} \left(−\mathrm{1}\right)^{{n}} }{−\mathrm{3}\:+{in}}\:\:−\frac{\mathrm{1}}{\mathrm{3}+{in}}\:−\frac{\mathrm{1}}{−\mathrm{3}+{in}} \\ $$$$=\frac{\left(\mathrm{3}−{in}\right)\:{e}^{\mathrm{3}\pi} \left(−\mathrm{1}\right)^{{n}} }{\mathrm{9}+{n}^{\mathrm{2}} }\:+\:\frac{\left(−\mathrm{3}−{in}\right){e}^{−\mathrm{3}\pi} \left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\mathrm{9}+\boldsymbol{{n}}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{3}+\boldsymbol{{in}}}\:+\frac{\mathrm{1}}{\mathrm{3}−\boldsymbol{{in}}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\mathrm{9}+\boldsymbol{{n}}^{\mathrm{2}} }\:\left\{\:\mathrm{3}\:\boldsymbol{{e}}^{\mathrm{3}\pi} \:−{in}\:{e}^{\mathrm{3}\pi} \:−\mathrm{3}\:{e}^{−\mathrm{3}\pi} \:−{in}\:{e}^{−\mathrm{3}\pi} \right\}\:+\frac{\mathrm{1}}{\mathrm{3}−{in}}\:−\frac{\mathrm{1}}{\mathrm{3}+{in}} \\ $$$$=\frac{\mathrm{3}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{9}+{n}^{\mathrm{2}} }\left\{\:{e}^{\mathrm{3}\pi} \:−{e}^{−\mathrm{3}\pi} \right\}\:−\frac{{n}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{9}+{n}^{\mathrm{2}} }{i}\:\left\{{e}^{\mathrm{3}\pi} \:+{e}^{−\mathrm{3}\pi} \right\}\:\:\:+\frac{\mathrm{2}{in}}{\mathrm{9}+{n}^{\mathrm{2}} } \\ $$$$\left.\Rightarrow\:{u}_{{n}} =\:\frac{\mathrm{3}\left(−\mathrm{1}\right)^{{n}} \left({e}^{\mathrm{3}\pi} \:−{e}^{−\mathrm{3}\pi} \right)}{\mathrm{9}+{n}^{\mathrm{2}} }\:\:\:\:{also}\:{we}\:{have}\:{v}_{{n}} =\:{Im}\left(\int_{\mathrm{0}} ^{\pi} \:{e}^{\left(\mathrm{3}+{in}\right){x}} \:+{e}^{\left(−\mathrm{3}+{in}\right){x}} \right){dx}\right) \\ $$$$\Rightarrow{v}_{{n}} =\frac{\mathrm{2}{n}\:−{n}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{9}+{n}^{\mathrm{2}} }\:. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 02/Sep/18
$${u}_{{n}} =\frac{\mathrm{3}\left(−\mathrm{1}\right)^{{n}} \left({e}^{\mathrm{3}\pi} \:−{e}^{−\mathrm{3}\pi} \right)}{\mathrm{2}\left(\mathrm{9}+{n}^{\mathrm{2}} \right)}\:\:\:{and}\:{v}_{{n}} =\:\frac{\mathrm{2}{n}−{n}\left(−\mathrm{1}\right)^{{n}} \left\{\:{e}^{\mathrm{3}\pi} \:+{e}^{−\mathrm{3}\pi} \right\}}{\mathrm{2}\left(\mathrm{9}+{n}^{\mathrm{2}} \right)} \\ $$