Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 42785 by maxmathsup by imad last updated on 02/Sep/18

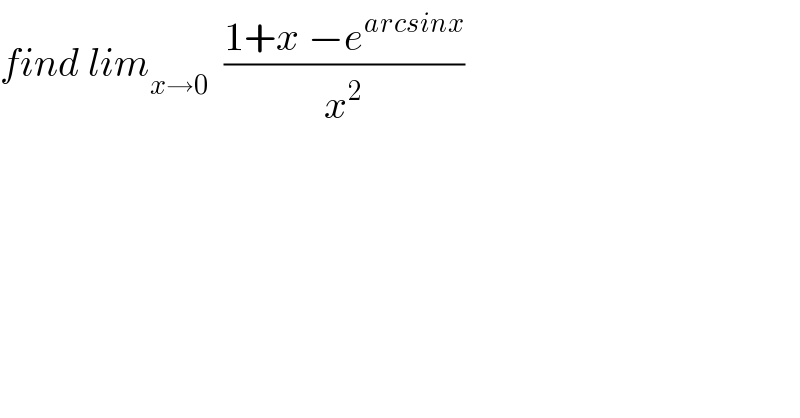
find lim_(x→0) ((1+x −e^(arcsinx) )/x^2 )

$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}+{x}\:−{e}^{{arcsinx}} }{{x}^{\mathrm{2}} } \\ $$

Commented by maxmathsup by imad last updated on 30/Sep/18

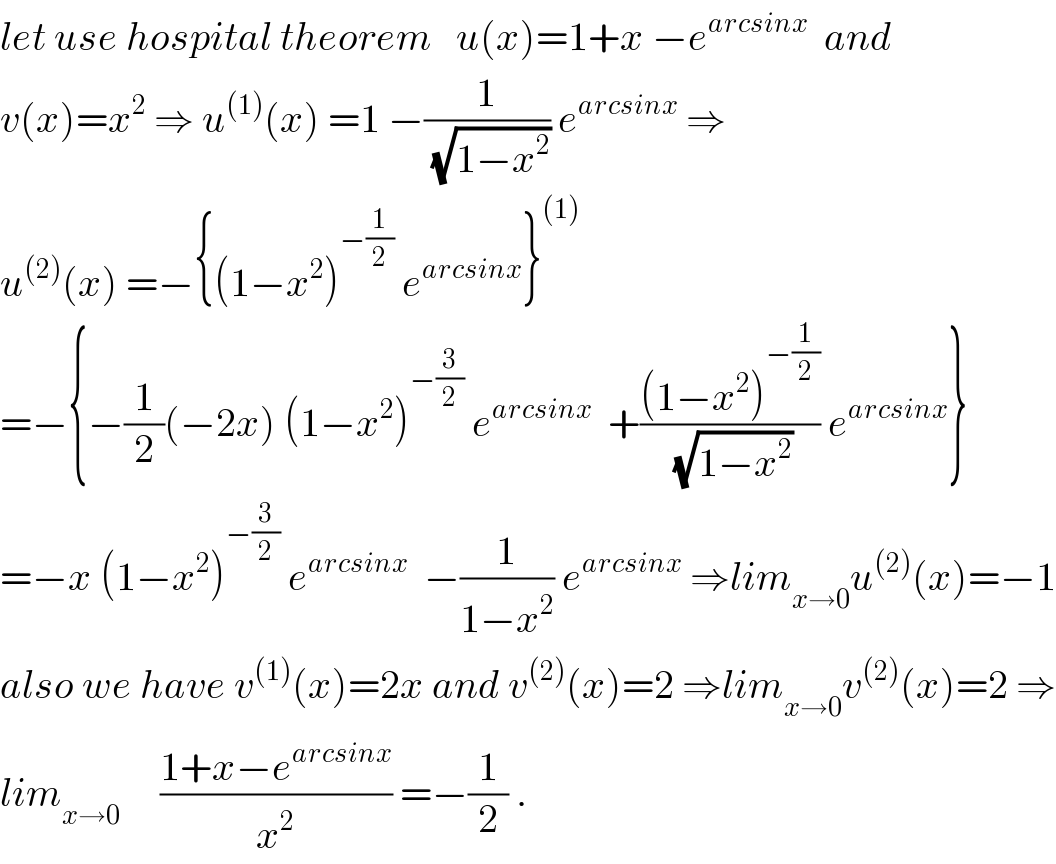
let use hospital theorem u(x)=1+x −e^(arcsinx) and v(x)=x^2 ⇒ u^((1)) (x) =1 −(1/(√(1−x^2 ))) e^(arcsinx) ⇒ u^((2)) (x) =−{(1−x^2 )^(−(1/2)) e^(arcsinx) }^((1)) =−{−(1/2)(−2x) (1−x^2 )^(−(3/2)) e^(arcsinx) +(((1−x^2 )^(−(1/2)) )/(√(1−x^2 ))) e^(arcsinx) } =−x (1−x^2 )^(−(3/2)) e^(arcsinx) −(1/(1−x^2 )) e^(arcsinx) ⇒lim_(x→0) u^((2)) (x)=−1 also we have v^((1)) (x)=2x and v^((2)) (x)=2 ⇒lim_(x→0) v^((2)) (x)=2 ⇒ lim_(x→0) ((1+x−e^(arcsinx) )/x^2 ) =−(1/2) .

$${let}\:{use}\:{hospital}\:{theorem}\:\:\:{u}\left({x}\right)=\mathrm{1}+{x}\:−{e}^{{arcsinx}} \:\:{and} \\ $$$${v}\left({x}\right)={x}^{\mathrm{2}} \:\Rightarrow\:{u}^{\left(\mathrm{1}\right)} \left({x}\right)\:=\mathrm{1}\:−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{e}^{{arcsinx}} \:\Rightarrow \\ $$$${u}^{\left(\mathrm{2}\right)} \left({x}\right)\:=−\left\{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{e}^{{arcsinx}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=−\left\{−\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{2}{x}\right)\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{{arcsinx}} \:\:+\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{e}^{{arcsinx}} \right\} \\ $$$$=−{x}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{{arcsinx}} \:\:−\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{e}^{{arcsinx}} \:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {u}^{\left(\mathrm{2}\right)} \left({x}\right)=−\mathrm{1} \\ $$$${also}\:{we}\:{have}\:{v}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{2}{x}\:{and}\:{v}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {v}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{\mathrm{1}+{x}−{e}^{{arcsinx}} }{{x}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18

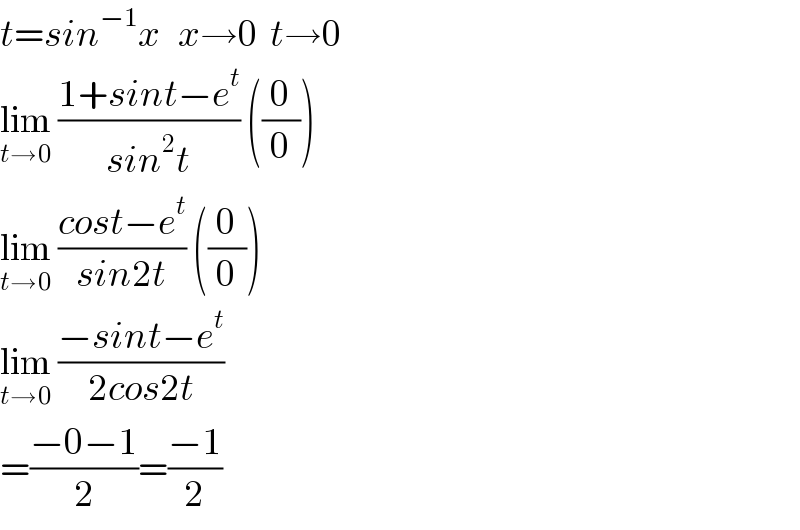
t=sin^(−1) x x→0 t→0 lim_(t→0) ((1+sint−e^t )/(sin^2 t)) ((0/0)) lim_(t→0) ((cost−e^t )/(sin2t)) ((0/0)) lim_(t→0) ((−sint−e^t )/(2cos2t)) =((−0−1)/2)=((−1)/2)

$${t}={sin}^{−\mathrm{1}} {x}\:\:\:{x}\rightarrow\mathrm{0}\:\:{t}\rightarrow\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+{sint}−{e}^{{t}} }{{sin}^{\mathrm{2}} {t}}\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{cost}−{e}^{{t}} }{{sin}\mathrm{2}{t}}\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{sint}−{e}^{{t}} }{\mathrm{2}{cos}\mathrm{2}{t}} \\ $$$$=\frac{−\mathrm{0}−\mathrm{1}}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com