Previous in Relation and Functions Next in Relation and Functions
Question Number 42805 by maxmathsup by imad last updated on 02/Sep/18
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:\:\:{with} \\ $$$${S}_{{n}} =\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}^{\mathrm{3}} }{\sqrt{\left(\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right)^{\mathrm{3}} }} \\ $$
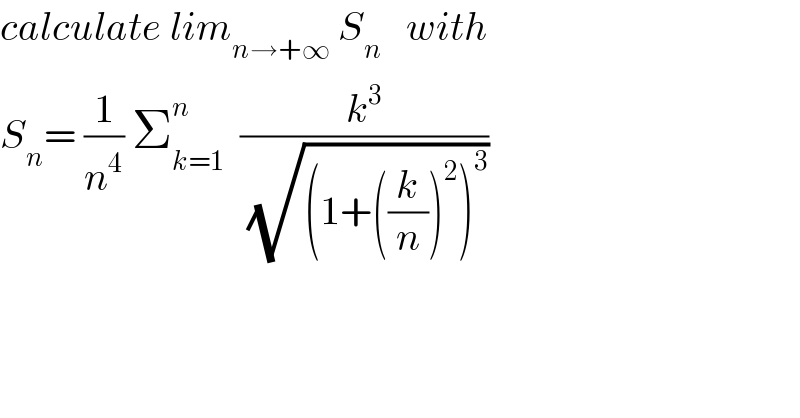
Commented by maxmathsup by imad last updated on 03/Sep/18
![we have S_n =(1/n) Σ_(k=1) ^n ((((k/n))^3 )/(√((1+((k/n))^2 )^3 ))) ⇒S_n is a Rieman sum and lim_(n→+∞) S_n = ∫_0 ^1 (x^3 /(√((1+x^2 )^3 )))dx = ∫_0 ^1 (x^3 /(((√(1+x^2 )))^3 ))dx changemen (√(1+x^2 ))=t give 1+x^2 =t^2 ⇒xdx =tdt ⇒ ∫_0 ^1 (x^3 /(((√(1+x^2 )^3 )))) dx = ∫_1 ^(√2) (((t^2 −1)tdt)/t^3 ) = ∫_1 ^(√2) ((t^3 −t)/t^3 )dt = ∫_1 ^(√2) (1−(1/t^2 )) =[t +(1/t)]_1 ^(√2) =(√2)+(1/(√2)) −2 =(3/(√2)) −2 ⇒ lim_(n→+∞) S_n = ((3−2(√2))/(√2)) .](Q42840.png)
$${we}\:{have}\:{S}_{{n}} =\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\left(\frac{{k}}{{n}}\right)^{\mathrm{3}} }{\sqrt{\left(\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right)^{\mathrm{3}} }}\:\Rightarrow{S}_{{n}} \:{is}\:{a}\:{Rieman}\:{sum}\:{and} \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{3}} }{\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\mathrm{3}} }{\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{3}} }{dx}\:{changemen}\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }={t} \\ $$$${give}\:\mathrm{1}+{x}^{\mathrm{2}} \:={t}^{\mathrm{2}} \:\Rightarrow{xdx}\:={tdt}\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{3}} }{\left(\sqrt{\left.\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\right.}\:{dx}\:=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right){tdt}}{{t}^{\mathrm{3}} } \\ $$$$=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{{t}^{\mathrm{3}} −{t}}{{t}^{\mathrm{3}} }{dt}\:=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\:=\left[{t}\:+\frac{\mathrm{1}}{{t}}\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:=\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:−\mathrm{2}\:=\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\:−\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =\:\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}}\:\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18
$${li}\underset{{n}\rightarrow\infty} {{m}S}_{{n}} ={lim}\:{n}\rightarrow\infty\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}}\frac{\left(\frac{{k}}{{n}}\right)^{\mathrm{3}} }{\sqrt{\left\{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right\}^{\mathrm{3}} }} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\sqrt{\left\{\mathrm{1}+{x}^{\mathrm{2}} \right\}^{\mathrm{3}} }}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}+{x}^{\mathrm{2}} \:\:\:{tdt}={xdx} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right){tdt}}{{t}^{\mathrm{3}} } \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:{dt} \\ $$$$\mid{t}+\frac{\mathrm{1}}{{t}}\mid_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \\ $$$$\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)+\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}−\sqrt{\mathrm{2}}\:+\mathrm{1}−\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}}=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}} \\ $$