Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 4281 by Filup last updated on 07/Jan/16

The following image shows the functiond f(x)=xe^(1/(1−x)) and g(x)=x−1 Can you explain as to why as ∣f(x)∣→∞, that f(x)→g(x).

$$\mathrm{The}\:\mathrm{following}\:\mathrm{image}\:\mathrm{shows}\:\mathrm{the}\:\mathrm{functiond} \\ $$$${f}\left({x}\right)={xe}^{\frac{\mathrm{1}}{\mathrm{1}−{x}}} \:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:{g}\left({x}\right)={x}−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{as}\:\mathrm{to}\:\mathrm{why}\:\mathrm{as}\:\mid{f}\left({x}\right)\mid\rightarrow\infty, \\ $$$$\mathrm{that}\:{f}\left({x}\right)\rightarrow{g}\left({x}\right). \\ $$

Commented by Filup last updated on 07/Jan/16

Commented by Filup last updated on 07/Jan/16

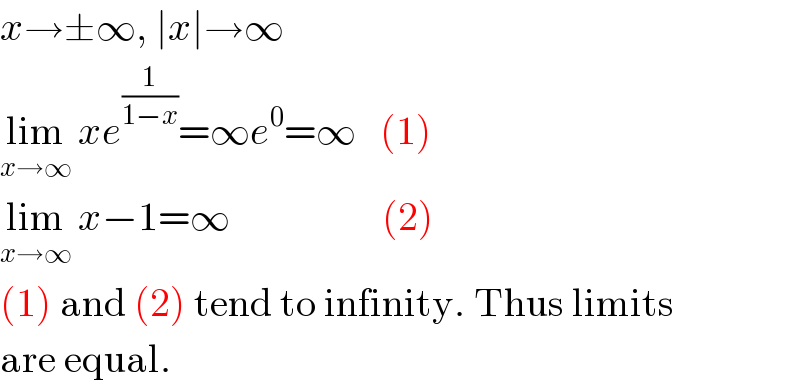
x→±∞, ∣x∣→∞ lim_(x→∞) xe^(1/(1−x)) =∞e^0 =∞ (1) lim_(x→∞) x−1=∞ (2) (1) and (2) tend to infinity. Thus limits are equal.

$${x}\rightarrow\pm\infty,\:\mid{x}\mid\rightarrow\infty \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{xe}^{\frac{\mathrm{1}}{\mathrm{1}−{x}}} =\infty{e}^{\mathrm{0}} =\infty\:\:\:\left(\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}−\mathrm{1}=\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{tend}\:\mathrm{to}\:\mathrm{infinity}.\:\mathrm{Thus}\:\mathrm{limits} \\ $$$$\mathrm{are}\:\mathrm{equal}. \\ $$

Commented by Yozzii last updated on 07/Jan/16

f(x)=xe^(1/(1−x)) (x≠1) f^′ (x)=e^((1−x)^(−1) ) +x×(1−x)^(−2) e^((1−x)^(−1) ) f^′ (x)=e^(1/(1−x)) (1+(x/((x−1)^2 ))) f^′ (x)=e^((1−x)^(−1) ) (((x^2 −x+1)/(x^2 −2x+1))) f^′ (x)=e^((1−x)^(−1) ) (((1−(1/x)+(1/x^2 ))/(1−(2/x)+(1/x^2 )))) ∴ l=lim_(x→∞) f^′ (x)=lim_(x→∞) {e^(1/(1−x)) (((1−(1/x)+(1/x^2 ))/(1−(2/x)+(1/x^2 ))))} l=e^(1/(−∞)) ((1−0+0)/(1−0+0))=1=g^′ (x) for x>1. So, the graph of f(x) is approximately parallel to that of g(x) for sufficiently large values of x. lnf(x)=lnx+(1/(1−x)) ∴lim_(x→1^+ ) lnf(x)=ln1−∞=−∞ ∴ lim_(x→1^+ ) f(x)=e^(−∞) =0 So, x=1 is the approximate root of f(x)=0. Also, lim_(x→∞) lnf(x)=∞⇒f(x)→∞ while f′(x)→1. So, a straight line approximates f(x) for large x. Given that f^′ (x)→1 as x→∞ for x>1 and x=1 is a root of f(x)=0, an asymptote to f(x) as x→∞ is found to be y−0=(1)(x−1)⇒y=x−1 which is the function g(x).

$${f}\left({x}\right)={xe}^{\frac{\mathrm{1}}{\mathrm{1}−{x}}} \:\:\:\:\left({x}\neq\mathrm{1}\right) \\ $$$${f}^{'} \left({x}\right)={e}^{\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} } +{x}×\left(\mathrm{1}−{x}\right)^{−\mathrm{2}} {e}^{\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} } \\ $$$${f}^{'} \left({x}\right)={e}^{\frac{\mathrm{1}}{\mathrm{1}−{x}}} \left(\mathrm{1}+\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$${f}^{'} \left({x}\right)={e}^{\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} } \left(\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}\right) \\ $$$${f}^{'} \left({x}\right)={e}^{\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} } \left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right) \\ $$$$\therefore\:{l}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}^{'} \left({x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{{e}^{\frac{\mathrm{1}}{\mathrm{1}−{x}}} \left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)\right\} \\ $$$${l}={e}^{\frac{\mathrm{1}}{−\infty}} \frac{\mathrm{1}−\mathrm{0}+\mathrm{0}}{\mathrm{1}−\mathrm{0}+\mathrm{0}}=\mathrm{1}={g}^{'} \left({x}\right)\:{for}\:{x}>\mathrm{1}. \\ $$$${So},\:{the}\:{graph}\:{of}\:{f}\left({x}\right)\:{is}\:{approximately} \\ $$$${parallel}\:{to}\:{that}\:{of}\:{g}\left({x}\right)\:{for}\:{sufficiently} \\ $$$${large}\:{values}\:{of}\:{x}. \\ $$$${lnf}\left({x}\right)={lnx}+\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{lnf}\left({x}\right)={ln}\mathrm{1}−\infty=−\infty \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{f}\left({x}\right)={e}^{−\infty} =\mathrm{0} \\ $$$${So},\:{x}=\mathrm{1}\:{is}\:{the}\:{approximate}\:{root}\:{of}\:{f}\left({x}\right)=\mathrm{0}. \\ $$$${Also},\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{lnf}\left({x}\right)=\infty\Rightarrow{f}\left({x}\right)\rightarrow\infty \\ $$$${while}\:{f}'\left({x}\right)\rightarrow\mathrm{1}.\:{So},\:{a}\:{straight}\:{line}\: \\ $$$${approximates}\:{f}\left({x}\right)\:{for}\:{large}\:{x}. \\ $$$${Given}\:{that}\:{f}^{'} \left({x}\right)\rightarrow\mathrm{1}\:{as}\:{x}\rightarrow\infty\:\:{for}\:{x}>\mathrm{1} \\ $$$${and}\:{x}=\mathrm{1}\:{is}\:{a}\:{root}\:{of}\:{f}\left({x}\right)=\mathrm{0},\:{an}\: \\ $$$${asymptote}\:{to}\:{f}\left({x}\right)\:{as}\:{x}\rightarrow\infty\:{is}\:{found}\:{to} \\ $$$${be}\:{y}−\mathrm{0}=\left(\mathrm{1}\right)\left({x}−\mathrm{1}\right)\Rightarrow{y}={x}−\mathrm{1}\:{which} \\ $$$${is}\:{the}\:{function}\:{g}\left({x}\right).\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com