
Question Number 4297 by 123456 last updated on 07/Jan/16
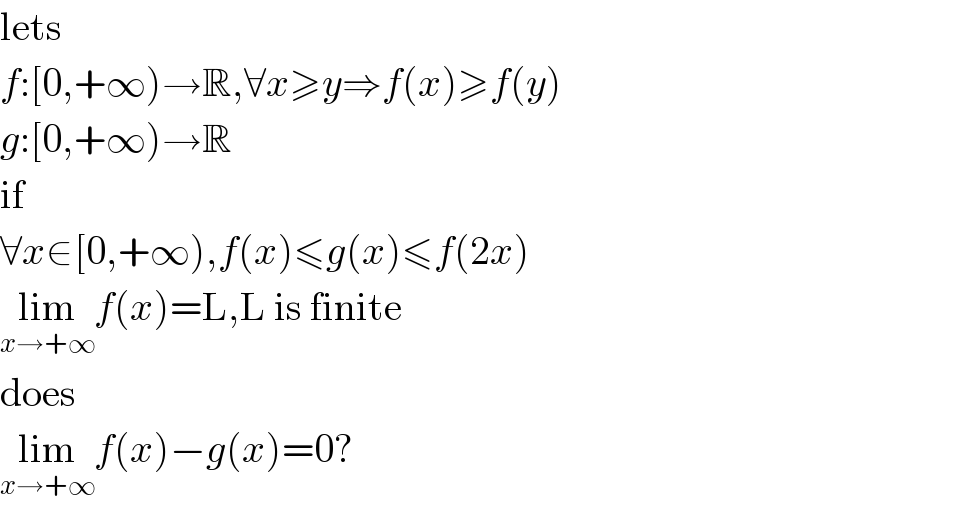
$$\mathrm{lets} \\ $$$${f}:\left[\mathrm{0},+\infty\right)\rightarrow\mathbb{R},\forall{x}\geqslant{y}\Rightarrow{f}\left({x}\right)\geqslant{f}\left({y}\right) \\ $$$${g}:\left[\mathrm{0},+\infty\right)\rightarrow\mathbb{R} \\ $$$$\mathrm{if} \\ $$$$\forall{x}\in\left[\mathrm{0},+\infty\right),{f}\left({x}\right)\leqslant{g}\left({x}\right)\leqslant{f}\left(\mathrm{2}{x}\right) \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{L},\mathrm{L}\:\mathrm{is}\:\mathrm{finite} \\ $$$$\mathrm{does} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)−{g}\left({x}\right)=\mathrm{0}? \\ $$
Commented by Yozzii last updated on 08/Jan/16

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left(\mathrm{2}{x}\right)=\underset{\mathrm{0}.\mathrm{5}{u}\rightarrow\infty} {\mathrm{lim}}{f}\left({u}\right)=\underset{{u}\rightarrow\infty} {\mathrm{lim}}{f}\left({u}\right)={L} \\ $$$${Since}\:{f}\left({x}\right)\leqslant{g}\left({x}\right)\leqslant{f}\left(\mathrm{2}{x}\right)\:\forall{x}\in\left[\mathrm{0},\infty\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}{g}\left({x}\right)\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left(\mathrm{2}{x}\right). \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left(\mathrm{2}{x}\right)={L}\:\Rightarrow\underset{{x}\rightarrow\infty} {\mathrm{lim}}{g}\left({x}\right)={L} \\ $$$${by}\:{the}\:{squeeze}\:{theorem}. \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{{f}\left({x}\right)−{g}\left({x}\right)\right\}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)−\underset{{x}\rightarrow\infty} {\mathrm{lim}}{g}\left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={L}−{L} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}. \\ $$$$\left({Under}\:{construction}\right) \\ $$$$ \\ $$
Commented by prakash jain last updated on 08/Jan/16

$${f}\left({x}\right)={x} \\ $$$${g}\left({x}\right)=\mathrm{1}.\mathrm{5}{x} \\ $$$${x}\geqslant\mathrm{0},\:{f}\left({x}\right)\leqslant{g}\left({x}\right)\leqslant{f}\left(\mathrm{2}{x}\right) \\ $$$${f}\left({x}\right)−{g}\left({x}\right)=−.\mathrm{5}{x} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)−{g}\left({x}\right)\neq\mathrm{0} \\ $$
Commented by Yozzii last updated on 08/Jan/16

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}=\infty\:\left({not}\:{finite}\right) \\ $$$${I}'{m}\:{searching}\:{for}\:{a}\:{counterexample} \\ $$$${as}\:{well}. \\ $$
Commented by prakash jain last updated on 08/Jan/16

$$\mathrm{oh}.\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{pay}\:\mathrm{attention}. \\ $$
Commented by prakash jain last updated on 08/Jan/16

$$\mathrm{You}\:\mathrm{are}\:\mathrm{correct}.\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)−{g}\left({x}\right)=\mathrm{0} \\ $$
