Question and Answers Forum
Question Number 43023 by ajfour last updated on 06/Sep/18

Commented by ajfour last updated on 06/Sep/18

Answered by MrW3 last updated on 07/Sep/18

Commented by MrW3 last updated on 07/Sep/18
![R sin γ=h sin θ ⇒sin γ=(h/R) sin θ with λ=(h/R) ⇒γ=sin^(−1) (λ sin θ) α=γ−θ β=γ+θ Δ_(OMD) =(h/2)×R sin α Δ_(OMC) =(h/2)×R sin β A_(OAD) =2×(h/2)×R sin α−αR^2 =((πR^2 )/3) ⇒(h/R) sin α−α=(π/3) ⇒λ sin [sin^(−1) (λ sin θ)−θ]−[sin^(−1) (λ sin θ)−θ]=(π/3) ...(i) A_(OBC) =2×(h/2)×R sin β+βR^2 =((2πR^2 )/3) ⇒(h/R) sin β+β=((2π)/3) ⇒λ sin [sin^(−1) (λ sin θ)+θ]+[sin^(−1) (λ sin θ)+θ]=((2π)/3) ...(ii) from (i) and (ii) we get λ and θ. I found a solution: λ=(h/R)≈5.763 θ≈2.64°](Q43099.png)
Commented by ajfour last updated on 07/Sep/18

Commented by ajfour last updated on 07/Sep/18

Commented by MrW3 last updated on 07/Sep/18
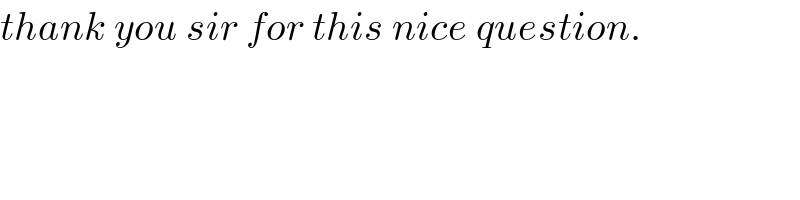
Commented by MrW3 last updated on 07/Sep/18

Commented by ajfour last updated on 07/Sep/18