Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 43027 by Raj Singh last updated on 06/Sep/18

Commented by math khazana by abdo last updated on 07/Sep/18

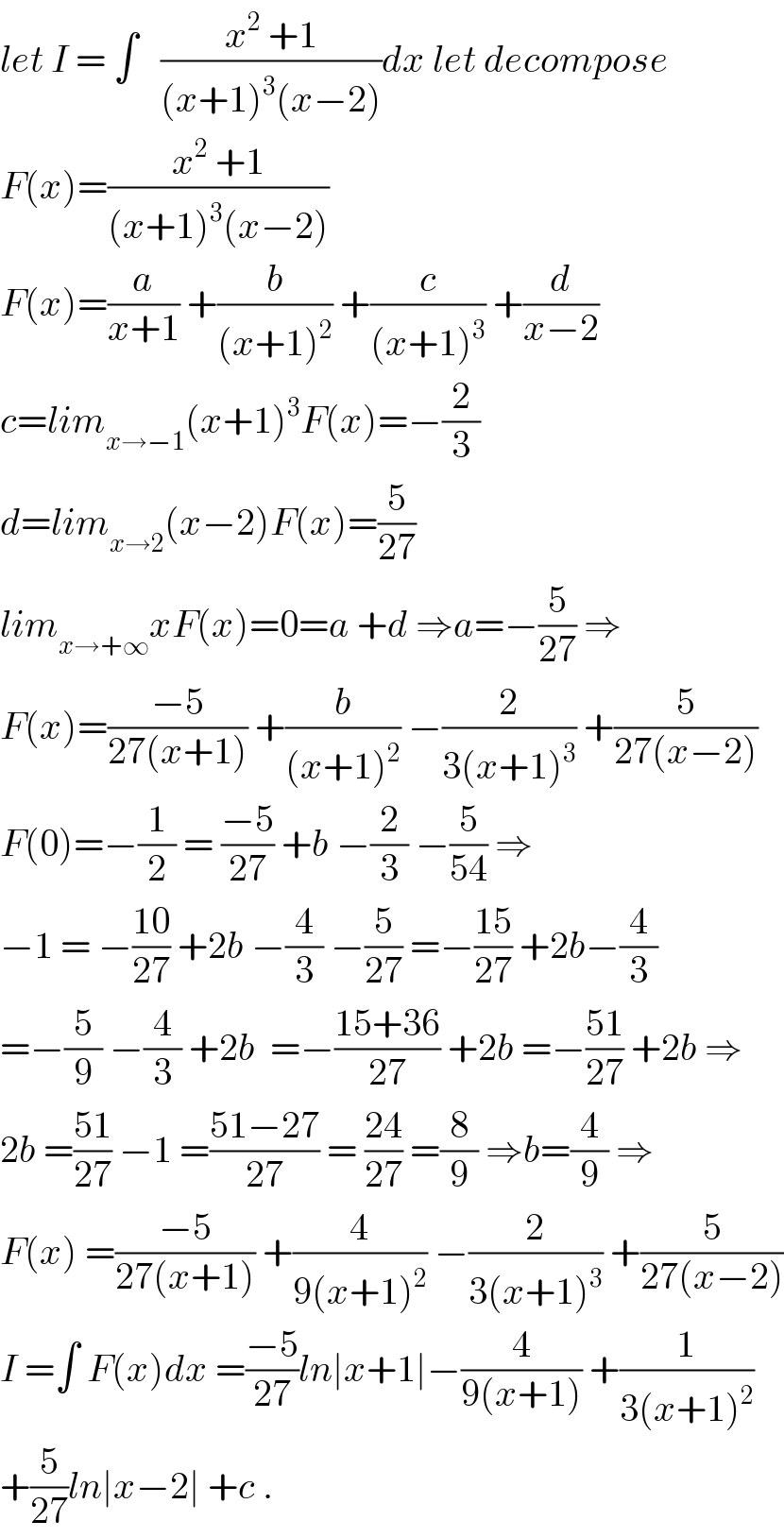
let I = ∫ ((x^2 +1)/((x+1)^3 (x−2)))dx let decompose F(x)=((x^2 +1)/((x+1)^3 (x−2))) F(x)=(a/(x+1)) +(b/((x+1)^2 )) +(c/((x+1)^3 )) +(d/(x−2)) c=lim_(x→−1) (x+1)^3 F(x)=−(2/3) d=lim_(x→2) (x−2)F(x)=(5/(27)) lim_(x→+∞) xF(x)=0=a +d ⇒a=−(5/(27)) ⇒ F(x)=((−5)/(27(x+1))) +(b/((x+1)^2 )) −(2/(3(x+1)^3 )) +(5/(27(x−2))) F(0)=−(1/2) = ((−5)/(27)) +b −(2/3) −(5/(54)) ⇒ −1 = −((10)/(27)) +2b −(4/3) −(5/(27)) =−((15)/(27)) +2b−(4/3) =−(5/9) −(4/3) +2b =−((15+36)/(27)) +2b =−((51)/(27)) +2b ⇒ 2b =((51)/(27)) −1 =((51−27)/(27)) = ((24)/(27)) =(8/9) ⇒b=(4/9) ⇒ F(x) =((−5)/(27(x+1))) +(4/(9(x+1)^2 )) −(2/(3(x+1)^3 )) +(5/(27(x−2))) I =∫ F(x)dx =((−5)/(27))ln∣x+1∣−(4/(9(x+1))) +(1/(3(x+1)^2 )) +(5/(27))ln∣x−2∣ +c .

$${let}\:{I}\:=\:\int\:\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)}{dx}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{b}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{{d}}{{x}−\mathrm{2}} \\ $$$${c}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right)^{\mathrm{3}} {F}\left({x}\right)=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${d}={lim}_{{x}\rightarrow\mathrm{2}} \left({x}−\mathrm{2}\right){F}\left({x}\right)=\frac{\mathrm{5}}{\mathrm{27}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}\:+{d}\:\Rightarrow{a}=−\frac{\mathrm{5}}{\mathrm{27}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{5}}{\mathrm{27}\left({x}+\mathrm{1}\right)}\:+\frac{{b}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{5}}{\mathrm{27}\left({x}−\mathrm{2}\right)} \\ $$$${F}\left(\mathrm{0}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{−\mathrm{5}}{\mathrm{27}}\:+{b}\:−\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{5}}{\mathrm{54}}\:\Rightarrow \\ $$$$−\mathrm{1}\:=\:−\frac{\mathrm{10}}{\mathrm{27}}\:+\mathrm{2}{b}\:−\frac{\mathrm{4}}{\mathrm{3}}\:−\frac{\mathrm{5}}{\mathrm{27}}\:=−\frac{\mathrm{15}}{\mathrm{27}}\:+\mathrm{2}{b}−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$=−\frac{\mathrm{5}}{\mathrm{9}}\:−\frac{\mathrm{4}}{\mathrm{3}}\:+\mathrm{2}{b}\:\:=−\frac{\mathrm{15}+\mathrm{36}}{\mathrm{27}}\:+\mathrm{2}{b}\:=−\frac{\mathrm{51}}{\mathrm{27}}\:+\mathrm{2}{b}\:\Rightarrow \\ $$$$\mathrm{2}{b}\:=\frac{\mathrm{51}}{\mathrm{27}}\:−\mathrm{1}\:=\frac{\mathrm{51}−\mathrm{27}}{\mathrm{27}}\:=\:\frac{\mathrm{24}}{\mathrm{27}}\:=\frac{\mathrm{8}}{\mathrm{9}}\:\Rightarrow{b}=\frac{\mathrm{4}}{\mathrm{9}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{−\mathrm{5}}{\mathrm{27}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{4}}{\mathrm{9}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{5}}{\mathrm{27}\left({x}−\mathrm{2}\right)} \\ $$$${I}\:=\int\:{F}\left({x}\right){dx}\:=\frac{−\mathrm{5}}{\mathrm{27}}{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{4}}{\mathrm{9}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$+\frac{\mathrm{5}}{\mathrm{27}}{ln}\mid{x}−\mathrm{2}\mid\:+{c}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18

2)∫log_(10) x dx =∫((log_e x)/(log_e 10))dx =(1/(ln10))∫lnxdx =(1/(ln10))[lnx×x−∫(1/x)×xdx] =(1/(ln10))[xlnx−x]+c

$$\left.\mathrm{2}\right)\int{log}_{\mathrm{10}} {x}\:{dx} \\ $$$$=\int\frac{{log}_{{e}} {x}}{{log}_{{e}} \mathrm{10}}{dx} \\ $$$$=\frac{\mathrm{1}}{{ln}\mathrm{10}}\int{lnxdx} \\ $$$$=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left[{lnx}×{x}−\int\frac{\mathrm{1}}{{x}}×{xdx}\right] \\ $$$$=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left[{xlnx}−{x}\right]+{c} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18

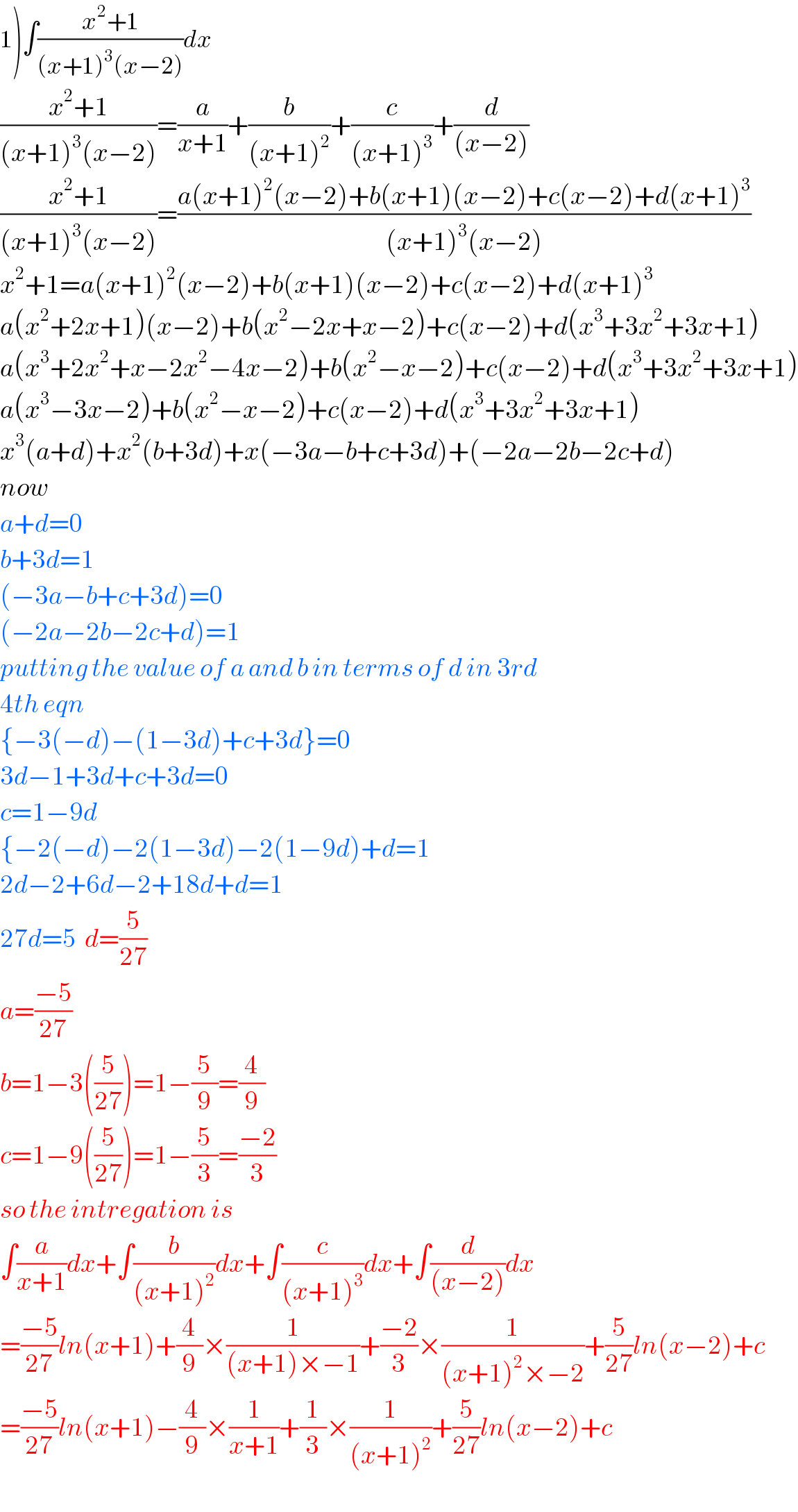
1)∫((x^2 +1)/((x+1)^3 (x−2)))dx ((x^2 +1)/((x+1)^3 (x−2)))=(a/(x+1))+(b/((x+1)^2 ))+(c/((x+1)^3 ))+(d/((x−2))) ((x^2 +1)/((x+1)^3 (x−2)))=((a(x+1)^2 (x−2)+b(x+1)(x−2)+c(x−2)+d(x+1)^3 )/((x+1)^3 (x−2))) x^2 +1=a(x+1)^2 (x−2)+b(x+1)(x−2)+c(x−2)+d(x+1)^3 a(x^2 +2x+1)(x−2)+b(x^2 −2x+x−2)+c(x−2)+d(x^3 +3x^2 +3x+1) a(x^3 +2x^2 +x−2x^2 −4x−2)+b(x^2 −x−2)+c(x−2)+d(x^3 +3x^2 +3x+1) a(x^3 −3x−2)+b(x^2 −x−2)+c(x−2)+d(x^3 +3x^2 +3x+1) x^3 (a+d)+x^2 (b+3d)+x(−3a−b+c+3d)+(−2a−2b−2c+d) now a+d=0 b+3d=1 (−3a−b+c+3d)=0 (−2a−2b−2c+d)=1 putting the value of a and b in terms of d in 3rd 4th eqn {−3(−d)−(1−3d)+c+3d}=0 3d−1+3d+c+3d=0 c=1−9d {−2(−d)−2(1−3d)−2(1−9d)+d=1 2d−2+6d−2+18d+d=1 27d=5 d=(5/(27)) a=((−5)/(27)) b=1−3((5/(27)))=1−(5/9)=(4/9) c=1−9((5/(27)))=1−(5/3)=((−2)/3) so the intregation is ∫(a/(x+1))dx+∫(b/((x+1)^2 ))dx+∫(c/((x+1)^3 ))dx+∫(d/((x−2)))dx =((−5)/(27))ln(x+1)+(4/9)×(1/((x+1)×−1))+((−2)/3)×(1/((x+1)^2 ×−2))+(5/(27))ln(x−2)+c =((−5)/(27))ln(x+1)−(4/9)×(1/(x+1))+(1/3)×(1/((x+1)^2 ))+(5/(27))ln(x−2)+c

$$\left.\mathrm{1}\right)\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)}{dx} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)}=\frac{{a}}{{x}+\mathrm{1}}+\frac{{b}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{c}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{{d}}{\left({x}−\mathrm{2}\right)} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)}=\frac{{a}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)+{b}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)+{c}\left({x}−\mathrm{2}\right)+{d}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}={a}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)+{b}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)+{c}\left({x}−\mathrm{2}\right)+{d}\left({x}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${a}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)+{b}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+{x}−\mathrm{2}\right)+{c}\left({x}−\mathrm{2}\right)+{d}\left({x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right) \\ $$$${a}\left({x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{2}\right)+{b}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)+{c}\left({x}−\mathrm{2}\right)+{d}\left({x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right) \\ $$$${a}\left({x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}\right)+{b}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)+{c}\left({x}−\mathrm{2}\right)+{d}\left({x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right) \\ $$$${x}^{\mathrm{3}} \left({a}+{d}\right)+{x}^{\mathrm{2}} \left({b}+\mathrm{3}{d}\right)+{x}\left(−\mathrm{3}{a}−{b}+{c}+\mathrm{3}{d}\right)+\left(−\mathrm{2}{a}−\mathrm{2}{b}−\mathrm{2}{c}+{d}\right) \\ $$$${now} \\ $$$${a}+{d}=\mathrm{0} \\ $$$${b}+\mathrm{3}{d}=\mathrm{1} \\ $$$$\left(−\mathrm{3}{a}−{b}+{c}+\mathrm{3}{d}\right)=\mathrm{0} \\ $$$$\left(−\mathrm{2}{a}−\mathrm{2}{b}−\mathrm{2}{c}+{d}\right)=\mathrm{1} \\ $$$${putting}\:{the}\:{value}\:{of}\:{a}\:{and}\:{b}\:{in}\:{terms}\:{of}\:{d}\:{in}\:\mathrm{3}{rd}\: \\ $$$$\mathrm{4}{th}\:{eqn} \\ $$$$\left\{−\mathrm{3}\left(−{d}\right)−\left(\mathrm{1}−\mathrm{3}{d}\right)+{c}+\mathrm{3}{d}\right\}=\mathrm{0} \\ $$$$\mathrm{3}{d}−\mathrm{1}+\mathrm{3}{d}+{c}+\mathrm{3}{d}=\mathrm{0} \\ $$$${c}=\mathrm{1}−\mathrm{9}{d} \\ $$$$\left\{−\mathrm{2}\left(−{d}\right)−\mathrm{2}\left(\mathrm{1}−\mathrm{3}{d}\right)−\mathrm{2}\left(\mathrm{1}−\mathrm{9}{d}\right)+{d}=\mathrm{1}\right. \\ $$$$\mathrm{2}{d}−\mathrm{2}+\mathrm{6}{d}−\mathrm{2}+\mathrm{18}{d}+{d}=\mathrm{1} \\ $$$$\mathrm{27}{d}=\mathrm{5}\:\:{d}=\frac{\mathrm{5}}{\mathrm{27}} \\ $$$${a}=\frac{−\mathrm{5}}{\mathrm{27}} \\ $$$${b}=\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{5}}{\mathrm{27}}\right)=\mathrm{1}−\frac{\mathrm{5}}{\mathrm{9}}=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$${c}=\mathrm{1}−\mathrm{9}\left(\frac{\mathrm{5}}{\mathrm{27}}\right)=\mathrm{1}−\frac{\mathrm{5}}{\mathrm{3}}=\frac{−\mathrm{2}}{\mathrm{3}} \\ $$$${so}\:{the}\:{intregation}\:{is} \\ $$$$\int\frac{{a}}{{x}+\mathrm{1}}{dx}+\int\frac{{b}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}+\int\frac{{c}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{dx}+\int\frac{{d}}{\left({x}−\mathrm{2}\right)}{dx} \\ $$$$=\frac{−\mathrm{5}}{\mathrm{27}}{ln}\left({x}+\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{9}}×\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)×−\mathrm{1}}+\frac{−\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} ×−\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{27}}{ln}\left({x}−\mathrm{2}\right)+{c} \\ $$$$=\frac{−\mathrm{5}}{\mathrm{27}}{ln}\left({x}+\mathrm{1}\right)−\frac{\mathrm{4}}{\mathrm{9}}×\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5}}{\mathrm{27}}{ln}\left({x}−\mathrm{2}\right)+{c} \\ $$

Commented by math khazana by abdo last updated on 07/Sep/18

your answer is correct sir Tanmay.

$${your}\:{answer}\:{is}\:{correct}\:{sir}\:{Tanmay}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18

thank you sir...

$${thank}\:{you}\:{sir}... \\ $$

Commented by malwaan last updated on 07/Sep/18

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com