Math Question and Answers


Question and Answers Forum

All Questions Topic List
Permutation and Combination Questions
Previous in All Question Next in All Question
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 43031 by aseerimad last updated on 06/Sep/18

Commented by MrW3 last updated on 06/Sep/18

$8! \times (9 + C_{2}^{9}) = 8! \times 45 = 5 \times 9! = 1814400$
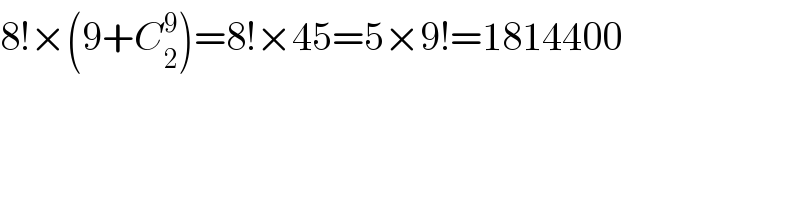
Commented by MrW3 last updated on 07/Sep/18

$E x p l a n a t i o n :$ $W e a r r a n g e a t f i r s t t h e o t h e r 8 s p e a k e r s,$ $t h e r e a r e 8! w a y s t o d o t h i s .$ $T h e r e a r e t w o m e t h o d s t o a r r a n g e t h e$ $s p e a k e r s A a n d B t h e n :$ $m e t h o d 1 : A a n d B a r e n e x t t o e a c h o t h e r . T h e r e$ $a r e 9 p o s s i b i l i t i e s . E . g . X X X X X X B A X X,$ $o r X X X X X X X X B A o r B A X X X X X X X X .$ $m e t h o d 2 : A a n d B a r e s e p a r a t e d b y a t$ $l e a s t o n e o f t h e o t h e r 8 p e o p l e . W e$ $c a n p l a c e A a n d B i n 9 p o s s i b l e p o s i t i o n s .$ $T h e r e a r e C_{2}^{9} w a y s . E . g . X X B X X X X A X X,$ $o r X X X X X X X B X A o r B X X X X X X X X A .$ $T h u s t h e r e s u l t i s$ $8! \times (9 + C_{2}^{9}) = 8! \times 45 = 5 \times 9!$ $G e n e r a l l y i n c a s e o f n p e o p l e :$ $(n - 2)! \times [(n - 1) + C_{2}^{n - 1}]$ $= (n - 2)! \times [(n - 1) + \frac{(n - 1) (n - 2)}{2}]$ $= \frac{n (n - 1) (n - 2)!}{2}$ $= \frac{n!}{2}$
	Answered by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18

	$a r r a n g e m e n t o f s p e a k e r l i k e$ $s u p o s e 1) B i s f i r s t s p e a k e r t h e n A c a n b e a n y$ $p o s i t i o n o u t o f r e m a i n i n g 9 s o$ $p e r m u t a t i o n i s 1 \times 9 \times 8!$ $h e r e 1 f o r B a n d 8! r e m a i n i n g 8 s p e a k e r$ $2) w h e n B s e c o n d s p e a k e r A c a n b e 3 r d 4 t h . . . 10 t h$ $s o 1 \times 8 \times 8!$ $3) w h e n B t h i r d s p e a k e r A c a n b e 4 t h 5 t h . . . 10 t h$ $1 \times 7 \times 8!$ $4) w h e n B 4 t h s p e a k e r A c a n b e 5 t h 6 t h . . . 10 t h$ $1 \times 6 \times 8!$ $5) w h e n B 5 t h s o e a k e r A c a n b e 6 t h 7 t h . . . 10 t h = 1$ $1 \times 5 \times 8!$ $6) w h e n B 6 t h s p e a k e r A c a n b e 7 t h 8 t h . . 10 t h$ $1 \times 4 \times 8!$ $7) w h e n B 7 t h s p e a k e r A c a n b e 8 t h 9 t h 10 t h$ $1 \times 3 \times 8!$ $8) w h e n B 8 t h s p e a k e r A [c a n b e [9 t h 10 t h$ $1 \times 2 \times 8!$ $9) w h e n B 9 t h s p e a k e r A c a n b e 10 t h$ $1 \times 1 \times 8!$ $s o a n s i s$ $1 \times 8! (9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1)$ $= 1 \times 8! \times \frac{9}{2} {2 \times 9 + (9 - 1) \times - 1}$ $= 1 \times 8! \times \frac{9}{2} (18 - 8)$ $= 8! \times 9 \times 5$ $= 9! \times 5$
	Answered by MrW3 last updated on 06/Sep/18

	$H e r e i s a n e a s y s o l u t i o n :$ $T o a r r a n g e 10 p e o p l e t h e r e a r e 10! w a y s .$ $T h e n u m b e r o f a r r a n g e m e n t s w i t h$ $A b e f o r e B i s t h e s a m e a s t h e n u m b e r$ $o f a r r a n g e m e n t s w i t h A b e h i n d B .$ $T h u s t h e s o l u t i o n i s \frac{10!}{2} = 1814400 .$
	Commented by ajfour last updated on 07/Sep/18

	$e x c e l l e n t S i r .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18

	$y e s s i r . . . t h a n k y o u . . .$
	Commented by malwaan last updated on 07/Sep/18

	$thank you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum