Question Number 43100 by maxmathsup by imad last updated on 07/Sep/18
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{cos}\theta}{\mathrm{1}+{xsin}\theta}{d}\theta \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+{xsin}\theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{values}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cos}\theta}{\mathrm{1}+\mathrm{2}{cos}\theta}{d}\theta\:\:\:{and}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+\mathrm{3}{sin}\theta\right)^{\mathrm{2}} }{d}\theta\:. \\ $$
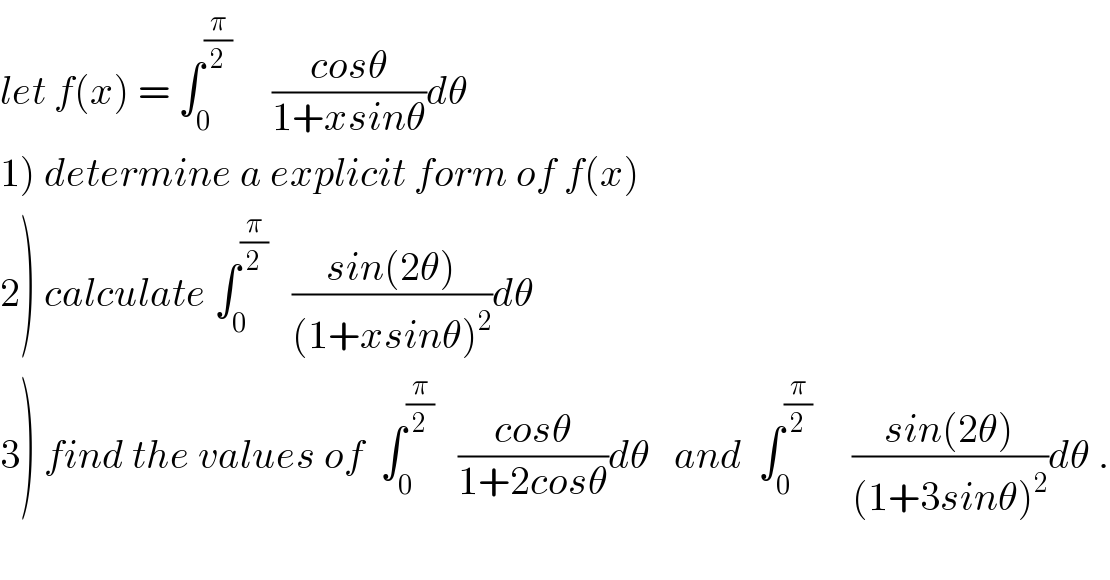
Commented by maxmathsup by imad last updated on 08/Sep/18
![1) x=0 ⇒f(x)=∫_0 ^(π/2) cosθ dθ =1 x≠0 ⇒ f(x)= (1/x) ∫_0 ^(π/2) ((xcosθ)/(1+xsinθ))dθ =(1/x)[ln∣1+xsinθ∣]_0 ^(π/2) =((ln∣1+x∣)/x) with x≠−1 and we must study the case x=−1 2) we have f^′ (x) = −∫_0 ^(π/2) ((sinθ cosθ)/((1+xsinθ)^2 ))dθ =−(1/2) ∫_0 ^(π/2) ((sin(2θ))/((1+xsinθ)^2 ))dθ ⇒ ∫_0 ^(π/2) ((sin(2θ))/((1+xsinθ)^2 ))dθ =−2f^′ (x) but f^′ (x)=−(1/x^2 )ln∣1+x∣ +(1/(x(1+x))) ⇒ ∫_0 ^(π/2) ((sin(2θ))/((1+xsinθ)^2 ))dθ =((2ln∣1+x∣)/x^2 ) −(2/(x(x+1))) .](Q43244.png)
$$\left.\mathrm{1}\right)\:{x}=\mathrm{0}\:\Rightarrow{f}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\theta\:{d}\theta\:=\mathrm{1} \\ $$$${x}\neq\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\frac{{xcos}\theta}{\mathrm{1}+{xsin}\theta}{d}\theta\:=\frac{\mathrm{1}}{{x}}\left[{ln}\mid\mathrm{1}+{xsin}\theta\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{{ln}\mid\mathrm{1}+{x}\mid}{{x}}\:{with} \\ $$$${x}\neq−\mathrm{1}\:\:\:{and}\:{we}\:{must}\:{study}\:{the}\:{case}\:{x}=−\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\theta\:{cos}\theta}{\left(\mathrm{1}+{xsin}\theta\right)^{\mathrm{2}} }{d}\theta\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+{xsin}\theta\right)^{\mathrm{2}} }{d}\theta\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+{xsin}\theta\right)^{\mathrm{2}} }{d}\theta\:=−\mathrm{2}{f}^{'} \left({x}\right)\:{but}\:\:{f}^{'} \left({x}\right)=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\mid\mathrm{1}+{x}\mid\:+\frac{\mathrm{1}}{{x}\left(\mathrm{1}+{x}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+{xsin}\theta\right)^{\mathrm{2}} }{d}\theta\:=\frac{\mathrm{2}{ln}\mid\mathrm{1}+{x}\mid}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{2}}{{x}\left({x}+\mathrm{1}\right)}\:. \\ $$
Commented by maxmathsup by imad last updated on 08/Sep/18
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cos}\theta}{\mathrm{1}+\mathrm{2}{sin}\theta}{d}\theta\:={f}\left(\mathrm{2}\right)=\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:\:{also}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\left(\mathrm{1}+\mathrm{3}{sin}\theta\right)^{\mathrm{2}} }\:=−\mathrm{2}{f}^{'} \left(\mathrm{3}\right)\:\:=\frac{\mathrm{2}{ln}\left(\mathrm{4}\right)}{\mathrm{9}}\:−\frac{\mathrm{2}}{\mathrm{12}}\:=\frac{\mathrm{4}{ln}\left(\mathrm{2}\right)}{\mathrm{9}}\:−\frac{\mathrm{1}}{\mathrm{6}}\:. \\ $$
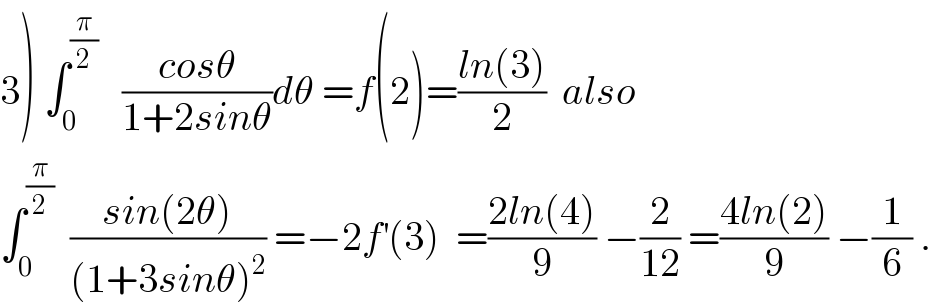
Answered by alex041103 last updated on 08/Sep/18
$${let}\:{u}=\mathrm{1}+{xsin}\theta \\ $$$${du}/{x}={cos}\theta\:{d}\theta \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\int_{\mathrm{1}} ^{\mathrm{1}+{x}} \frac{{du}}{{u}}=\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}={f}\left({x}\right) \\ $$