
Question and Answers Forum
Question Number 43131 by ajfour last updated on 07/Sep/18
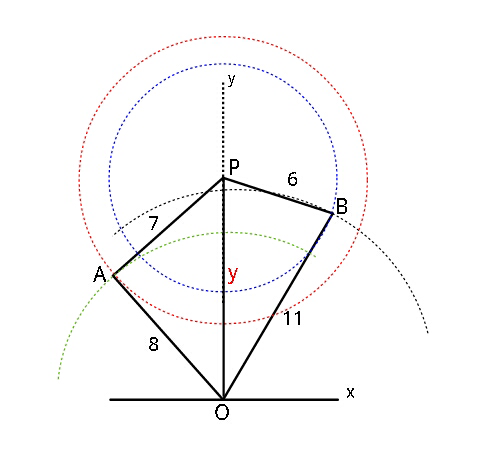
Commented by ajfour last updated on 07/Sep/18
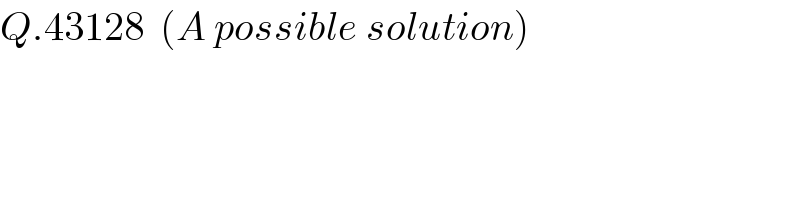
Answered by ajfour last updated on 07/Sep/18
![Area=(y/2)[(√(64−(((15)/(2y))+(y/2))^2 )) +(√(121−(((85)/(2y))+(y/2))^2 )) ] where y∈ [5,15] .](Q43134.png)
Answered by ajfour last updated on 07/Sep/18
![let presently OP = y = b point A is intersection of x^2 +y^2 =64 and x^2 +(y−b)^2 =49 ⇒ b(2y_A −b)=15 y_A =((15)/(2b))+(b/2) ⇒ x_A =(√(64−(((15)/(2b))+(b/2))^2 )) ..(i) point B is the intersection of x^2 +y^2 =121 and x^2 +(y−b)^2 =36 ⇒ b(2y_B −b)=85 y_B =((85)/(2b))+(b/2) ⇒ x_B = (√(121−(((85)/(2b))+(b/2))^2 )) Area = (b/2)(x_A +x_B ) Area = (b/2)[(√(64−(((15)/(2b))+(b/2))^2 )) +(√(121−(((85)/(2b))+(b/2))^2 )) ] Replacing b by y Area = (y/2)[(√(64−(((15)/(2y))+(y/2))^2 )) +(√(121−(((85)/(2y))+(y/2))^2 )) ].](Q43140.png)
| ||
Question and Answers Forum | ||
Question Number 43131 by ajfour last updated on 07/Sep/18 | ||
 | ||
Commented by ajfour last updated on 07/Sep/18 | ||
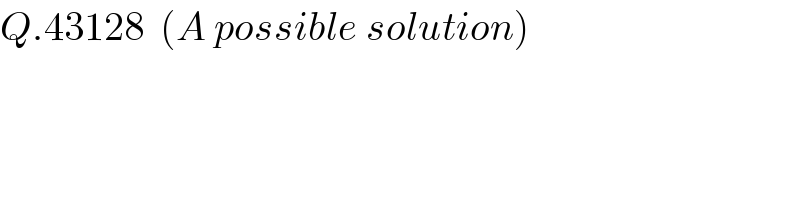 | ||
Answered by ajfour last updated on 07/Sep/18 | ||
![Area=(y/2)[(√(64−(((15)/(2y))+(y/2))^2 )) +(√(121−(((85)/(2y))+(y/2))^2 )) ] where y∈ [5,15] .](Q43134.png) | ||
| ||
Answered by ajfour last updated on 07/Sep/18 | ||
![let presently OP = y = b point A is intersection of x^2 +y^2 =64 and x^2 +(y−b)^2 =49 ⇒ b(2y_A −b)=15 y_A =((15)/(2b))+(b/2) ⇒ x_A =(√(64−(((15)/(2b))+(b/2))^2 )) ..(i) point B is the intersection of x^2 +y^2 =121 and x^2 +(y−b)^2 =36 ⇒ b(2y_B −b)=85 y_B =((85)/(2b))+(b/2) ⇒ x_B = (√(121−(((85)/(2b))+(b/2))^2 )) Area = (b/2)(x_A +x_B ) Area = (b/2)[(√(64−(((15)/(2b))+(b/2))^2 )) +(√(121−(((85)/(2b))+(b/2))^2 )) ] Replacing b by y Area = (y/2)[(√(64−(((15)/(2y))+(y/2))^2 )) +(√(121−(((85)/(2y))+(y/2))^2 )) ].](Q43140.png) | ||
| ||