
Question Number 4314 by Filup last updated on 09/Jan/16
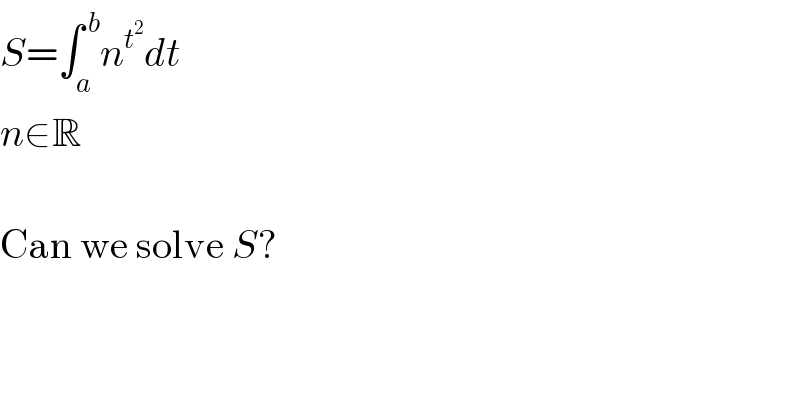
$${S}=\int_{{a}} ^{\:{b}} {n}^{{t}^{\mathrm{2}} } {dt} \\ $$$${n}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{solve}\:{S}? \\ $$
Commented by Filup last updated on 09/Jan/16
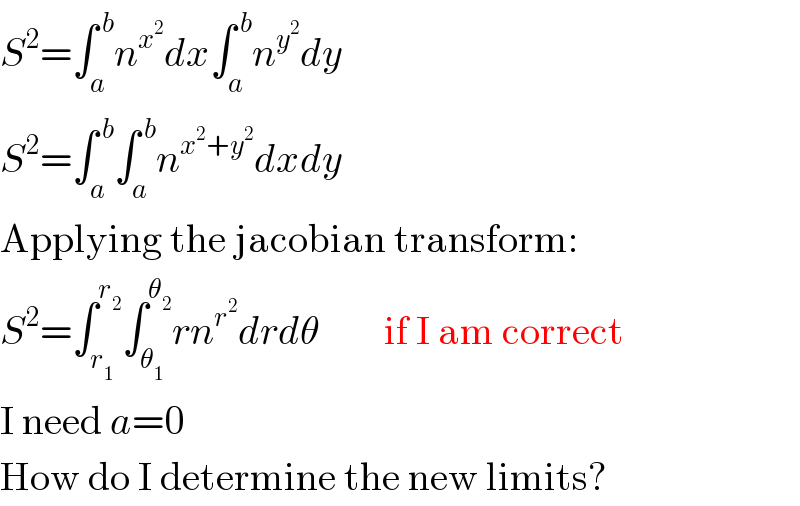
$${S}^{\mathrm{2}} =\int_{{a}} ^{\:{b}} {n}^{{x}^{\mathrm{2}} } {dx}\int_{{a}} ^{\:{b}} {n}^{{y}^{\mathrm{2}} } {dy} \\ $$$${S}^{\mathrm{2}} =\int_{{a}} ^{\:{b}} \int_{{a}} ^{\:{b}} {n}^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } {dxdy} \\ $$$$\mathrm{Applying}\:\mathrm{the}\:\mathrm{jacobian}\:\mathrm{transform}: \\ $$$${S}^{\mathrm{2}} =\int_{{r}_{\mathrm{1}} } ^{{r}_{\mathrm{2}} } \int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } {rn}^{{r}^{\mathrm{2}} } {drd}\theta\:\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{I}\:\mathrm{am}\:\mathrm{correct} \\ $$$$\mathrm{I}\:\mathrm{need}\:{a}=\mathrm{0} \\ $$$$\mathrm{How}\:\mathrm{do}\:\mathrm{I}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{new}\:\mathrm{limits}? \\ $$
Commented by prakash jain last updated on 10/Jan/16

$$\mathrm{Limit}\:\mathrm{on}\:{r}\:\mathrm{will}\:\mathrm{be}\:\mathrm{dependent}\:\mathrm{on}\:\theta.\:\mathrm{Basically} \\ $$$$\theta\:\mathrm{will}\:\mathrm{be}\:\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\mathrm{2}\pi.\:{r}\:\mathrm{can}\:\mathrm{be}\:\mathrm{found}\:\mathrm{based} \\ $$$$\mathrm{on}\:\mathrm{square}\:\mathrm{in}\:\mathrm{polar}\:\mathrm{coordinates}. \\ $$
