
Question and Answers Forum
Question Number 43147 by rahul 19 last updated on 07/Sep/18
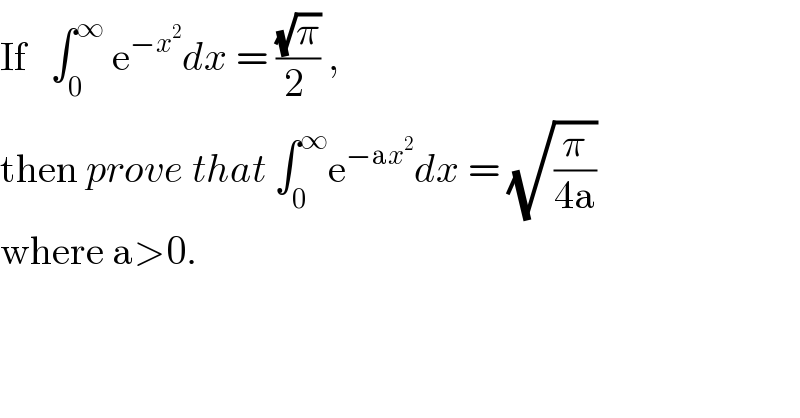
Commented byMrW3 last updated on 07/Sep/18
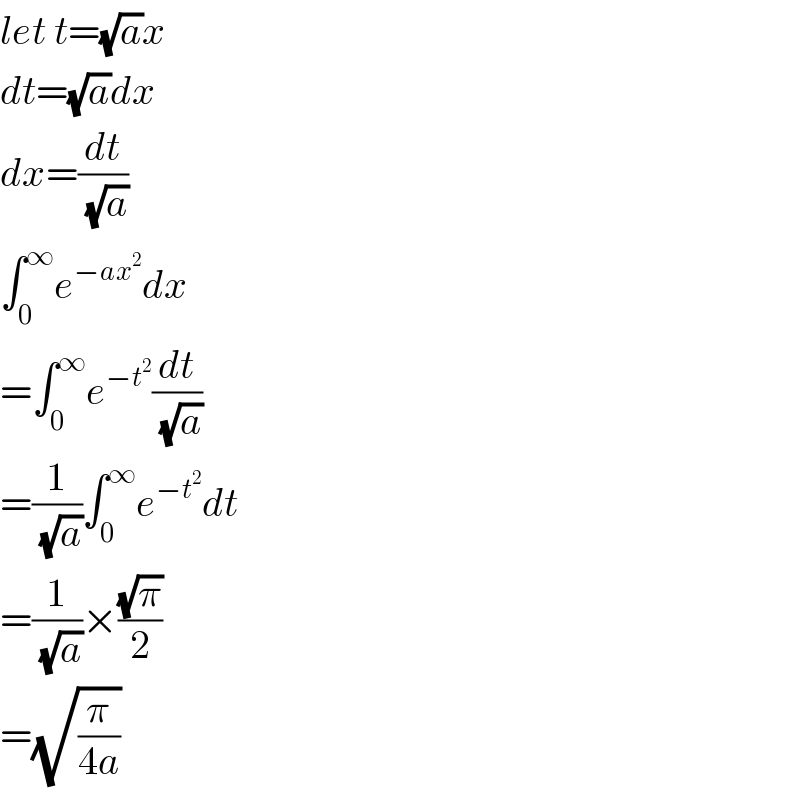
Commented byrahul 19 last updated on 07/Sep/18
thank you sir ��
| ||
Question and Answers Forum | ||
Question Number 43147 by rahul 19 last updated on 07/Sep/18 | ||
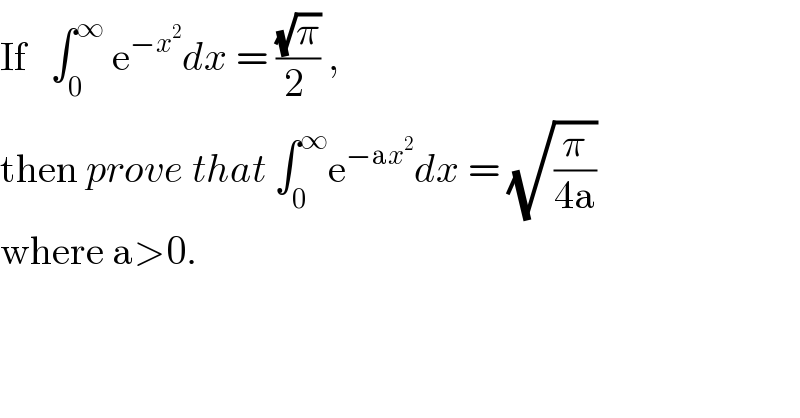 | ||
Commented byMrW3 last updated on 07/Sep/18 | ||
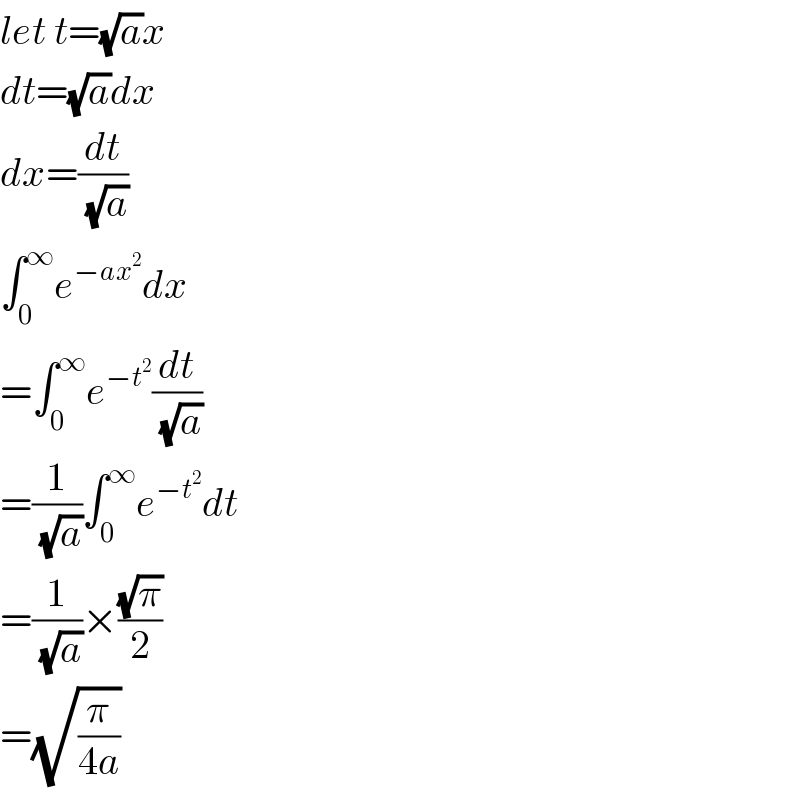 | ||
Commented byrahul 19 last updated on 07/Sep/18 | ||
thank you sir �� | ||