∫secxdx ?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 63976 by Scientist0000001 last updated on 11/Jul/19

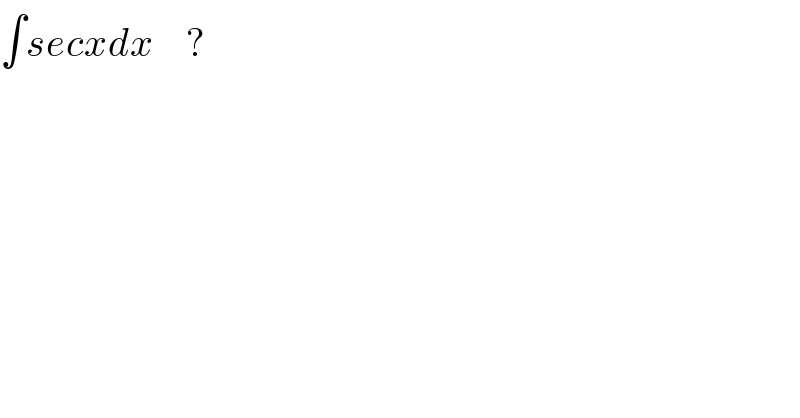
$\int s e c x d x ?$
Commented by Prithwish sen last updated on 12/Jul/19

$\int \frac{\sec^{2} \frac{x}{2}}{1 - \tan^{2} \frac{x}{2}} dx putting \tan \frac{x}{2} = t$ $\sec^{2} \frac{x}{2} dx = 2 dt ∴ 2 \int \frac{dt}{1 - t^{2}} = \int [\frac{1}{1 - t} + \frac{1}{1 + t}] dt$ $= \ln ∣ \frac{1 + t}{1 - t} ∣ + C$
Commented by hknkrc46 last updated on 11/Jul/19
$∫secxdx=∫(dx/(cosx))=∫((cosx)/(cos^2 x))dx=∫((cosx)/(1−sin^2 x))dx sinx=u⇒cosxdx=du ∫(du/(1−u^2 ))=(1/2)∫(((1−u)+(1+u))/((1−u)(1+u)))du =(1/2)[∫((1−u)/((1−u)(1+u)))du+∫((1+u)/((1−u)(1+u)))du] =(1/2)[∫(du/(1+u))+∫(du/(1−u))]=(1/2)[ln (1+u)−ln (1−u)]+c =(1/2)ln (((1+u)/(1−u)))+c=(1/2)ln (((1+sinx)/(1−sinx)))+c ★ =(1/2)ln ((((1+sinx)^2 )/((1+sinx)(1−sinx))))+c =(1/2)ln ((((1+sinx)^2 )/(1−sin^2 x)))+c =(1/2)ln ((((1+sinx)^2 )/(cos^2 x)))+c=ln (((1+sinx)/(cosx)))+c =ln ((1/(cosx))+((sinx)/(cosx)))+c=ln (secx+tanx)+c ★★ =ln (secx+tanx)+ln e^c =ln (e^c (secx+tanx)) =ln (c_1 (secx+tanx)) ★★★ {c , c_1 ∈R }$
$\int s e c x d x = \int \frac{d x}{c o s x} = \int \frac{c o s x}{{c o s}^{2} x} d x = \int \frac{c o s x}{1 - {s i n}^{2} x} d x$ $s i n x = u \Rightarrow c o s x d x = d u$ $\int \frac{d u}{1 - u^{2}} = \frac{1}{2} \int \frac{(1 - u) + (1 + u)}{(1 - u) (1 + u)} d u$ $= \frac{1}{2} [\int \frac{1 - u}{(1 - u) (1 + u)} d u + \int \frac{1 + u}{(1 - u) (1 + u)} d u]$ $= \frac{1}{2} [\int \frac{d u}{1 + u} + \int \frac{d u}{1 - u}] = \frac{1}{2} [\ln (1 + u) - \ln (1 - u)] + c$ $= \frac{1}{2} \ln (\frac{1 + u}{1 - u}) + c = \frac{1}{2} \ln (\frac{1 + s i n x}{1 - s i n x}) + c ★$ $= \frac{1}{2} \ln (\frac{{(1 + s i n x)}^{2}}{(1 + s i n x) (1 - s i n x)}) + c$ $= \frac{1}{2} \ln (\frac{{(1 + s i n x)}^{2}}{1 - {s i n}^{2} x}) + c$ $= \frac{1}{2} \ln (\frac{{(1 + s i n x)}^{2}}{{c o s}^{2} x}) + c = \ln (\frac{1 + s i n x}{c o s x}) + c$ $= \ln (\frac{1}{c o s x} + \frac{s i n x}{c o s x}) + c = \ln (s e c x + t a n x) + c ★ ★$ $= \ln (s e c x + t a n x) + \ln e^{c} = \ln (e^{c} (s e c x + t a n x))$ $= \ln (c_{1} (s e c x + t a n x)) ★ ★ ★$ ${c, c_{1} \in R}$
Commented by mathmax by abdo last updated on 11/Jul/19

$l e t I = \int \frac{d x}{c o s x} c h a n g e m e n t t a n (\frac{x}{2}) = t g i v e$ $I = \int \frac{2 d t}{(1 + t^{2}) \frac{1 - t^{2}}{1 + t^{2}}} = \int \frac{2 d t}{1 - t^{2}} = \int (\frac{1}{1 - t} + \frac{1}{1 + t}) d t$ $l n ∣ \frac{1 + t}{1 - t} ∣ + c = l n ∣ \frac{1 + t a n (\frac{x}{2})}{1 - t a n (\frac{x}{2})} ∣ + c = l n ∣ t a n (\frac{π}{4} + \frac{x}{2}) ∣ + c .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum