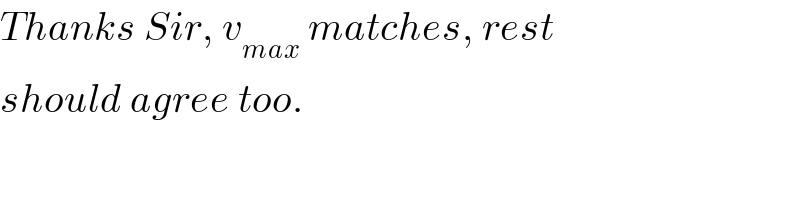Question Number 43187 by ajfour last updated on 08/Sep/18
Commented by ajfour last updated on 08/Sep/18
$${mass}\:{of}\:\left({toy}+{fuel}\right)=\:{M}+{m} \\ $$$${exhaust}\:{speed}\:\left({relative}\right)\:=\:{u} \\ $$$${friction}\:{coefficient}\:=\mu \\ $$$${Find}\:\left(\boldsymbol{{i}}\right)\:\boldsymbol{{maximum}}\:\boldsymbol{{velocity}} \\ $$$$\left(\boldsymbol{{ii}}\right)\:\boldsymbol{{Determine}}\:\boldsymbol{{how}}\:\boldsymbol{{far}}\:\boldsymbol{{can}}\:\boldsymbol{{it}}\:\boldsymbol{{go}}. \\ $$
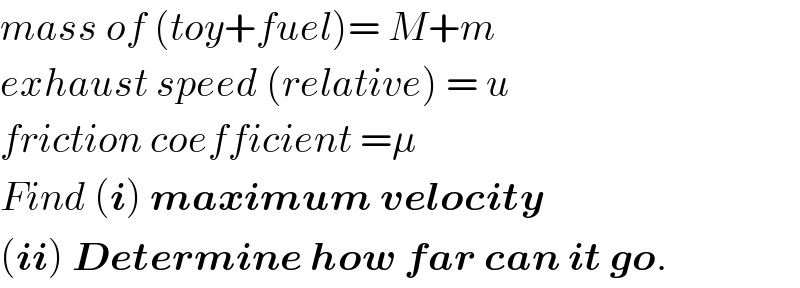
Answered by ajfour last updated on 08/Sep/18
![Case 1: (fuel over at t=t_1 , toy stops at t=t_2 ) let initial mass of fuel be m_0 M+m_0 = M_0 (M+m)(dv/dt)= −μN+q(ucos θ) N=(M+m)g+qusin θ ⇒ (dv/dt)= −μg+((qu(cos θ−μsin θ))/(M+m_0 −qt)) let λ=cos θ−μsin θ ⇒ ∫_0 ^( v) dv = −μgt+λuln ((M_0 /(M_0 −qt))) displacement s for this accelerating period is s=−((𝛍gt^2 )/2)+𝛌u∫_0 ^( t) ln ((M_0 /(M_0 −qt)))dt ∫_0 ^( t) ln ((M_0 /(M_0 −qt)))dt=tln ((M_0 /(M_0 −qt)))∣_0 ^t −∫_0 ^( t) t((q/(M_0 −qt)))dt =tln ((M_0 /(M_0 −qt)))+t+(M_0 /q)ln (((M_0 −qt)/M_0 )) ⇒ s_1 =λu[(m_0 /q)−(((M_0 −m_0 ))/q)ln ((M_0 /M))] −((μgm_0 ^2 )/(2q^2 )) Now t_1 = (m_0 /q) v_(max) = −((𝛍gm_0 )/q)+𝛌uln (((M+m_0 )/M)) hereafter s_2 =(v_(max) ^2 /(2𝛍g)) Total distance traveled is = s_1 +s_2 .](Q43247.png)
$${Case}\:\mathrm{1}:\:\left({fuel}\:{over}\:{at}\:{t}={t}_{\mathrm{1}} ,\right. \\ $$$$\left.{toy}\:{stops}\:{at}\:{t}={t}_{\mathrm{2}} \right) \\ $$$${let}\:{initial}\:{mass}\:{of}\:{fuel}\:{be}\:\boldsymbol{{m}}_{\mathrm{0}} \\ $$$${M}+{m}_{\mathrm{0}} =\:{M}_{\mathrm{0}} \\ $$$$\left({M}+{m}\right)\frac{{dv}}{{dt}}=\:−\mu{N}+{q}\left({u}\mathrm{cos}\:\theta\right) \\ $$$${N}=\left({M}+{m}\right){g}+{qu}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\frac{{dv}}{{dt}}=\:−\mu{g}+\frac{{qu}\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)}{{M}+{m}_{\mathrm{0}} −{qt}} \\ $$$${let}\:\:\lambda=\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\int_{\mathrm{0}} ^{\:\:{v}} {dv}\:=\:−\mu{gt}+\lambda{u}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right) \\ $$$${displacement}\:\boldsymbol{{s}}\:{for}\:{this}\:{accelerating} \\ $$$${period}\:{is} \\ $$$$\:\boldsymbol{{s}}=−\frac{\boldsymbol{\mu{gt}}^{\mathrm{2}} }{\mathrm{2}}+\boldsymbol{\lambda{u}}\int_{\mathrm{0}} ^{\:\:\boldsymbol{{t}}} \mathrm{ln}\:\left(\frac{\boldsymbol{{M}}_{\mathrm{0}} }{\boldsymbol{{M}}_{\mathrm{0}} −\boldsymbol{{qt}}}\right)\boldsymbol{{dt}} \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\:{t}} \mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right){dt}={t}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right)\mid_{\mathrm{0}} ^{{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\int_{\mathrm{0}} ^{\:\:{t}} {t}\left(\frac{{q}}{{M}_{\mathrm{0}} −{qt}}\right){dt} \\ $$$$\:\:={t}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right)+{t}+\frac{{M}_{\mathrm{0}} }{{q}}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} −{qt}}{{M}_{\mathrm{0}} }\right) \\ $$$$\Rightarrow\:\boldsymbol{{s}}_{\mathrm{1}} =\lambda{u}\left[\frac{{m}_{\mathrm{0}} }{{q}}−\frac{\left({M}_{\mathrm{0}} −{m}_{\mathrm{0}} \right)}{{q}}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mu{gm}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}{q}^{\mathrm{2}} } \\ $$$${Now}\:{t}_{\mathrm{1}} =\:\frac{{m}_{\mathrm{0}} }{{q}} \\ $$$$\boldsymbol{{v}}_{\boldsymbol{{max}}} =\:−\frac{\boldsymbol{\mu{gm}}_{\mathrm{0}} }{\boldsymbol{{q}}}+\boldsymbol{\lambda{u}}\mathrm{ln}\:\left(\frac{\boldsymbol{{M}}+\boldsymbol{{m}}_{\mathrm{0}} }{\boldsymbol{{M}}}\right) \\ $$$$\:\:\:\:\:\:\: \\ $$$${hereafter} \\ $$$$\boldsymbol{{s}}_{\mathrm{2}} =\frac{\boldsymbol{{v}}_{\boldsymbol{{max}}} ^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mu{g}}}\: \\ $$$${Total}\:{distance}\:{traveled}\:{is} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\boldsymbol{{s}}_{\mathrm{1}} +\boldsymbol{{s}}_{\mathrm{2}} \:. \\ $$
Commented by MrW3 last updated on 08/Sep/18
$${all}\:{correct}\:{sir}! \\ $$
Answered by MrW3 last updated on 08/Sep/18
![let m_0 =mass of fuel at t=0 let′s say at t=t_1 tank is empty. and it stops at t=t_2 0≤t≤t_1 : motion with variable mass M+m t_1 ≤t≤t_2 : motion with constant mass M in following it is assumed that the friction is so small as well as u and q are so large that the toy starts to move at t=0, see condition (I). (M+m)g−N−u sin θ ((d(M+m))/dt)=0 ⇒N=(M+m)g+uq sin θ −Nμ−u cos θ ((d(M+m))/dt)=(M+m)(dv/dt) ⇒−(M+m)μg+(cos θ−μ sin θ)uq=(M+m)(dv/dt) ⇒(M+m)(μg+(dv/dt))=uq(cos θ−μ sin θ) m=m_0 −qt ⇒(M+m_0 −qt)(μg+(dv/dt))=uq(cos θ−μ sin θ) ⇒(dv/dt)=((uq(cos θ−μ sin θ))/(M+m_0 −qt))−μg let M_0 =M+m_0 , λ=cos θ−μ sin θ ⇒a=(dv/dt)=((uqλ)/(M_0 −qt))−μg so that the toy starts to move at t=0, ((uqλ)/M_0 )−μg≥0 ⇒uq≥((μgM_0 )/λ)=((μg(M+m_0 ))/(cos θ−μ sin θ)) ...(I) ∫_0 ^v dv=∫_0 ^t (((uqλ)/(M_0 −qt))−μg)dt ⇒v=[−uλ ln (M_0 −qt)−μgt]_0 ^t ⇒v(t)=uλ ln (M_0 /(M_0 −qt))−μgt this is valid for t≤t_1 =(m_0 /q)=moment when tank is empty v_1 =v(t_1 )=uλ ln (M_0 /M)−((μgm_0 )/q) for t>t_1 : −μMg=M(dv/dt) ⇒(dv/dt)=−μg ∫_v_1 ^v dv=−∫_t_1 ^t μgdt v(t)−v_1 =−μg(t−t_1 ) ⇒v(t)=v_1 −μg(t−t_1 ) at t=t_2 : v=0 uλ ln (M_0 /M)−((μgm_0 )/q)−μg(t_2 −(m_0 /q))=0 t_2 =((uλ)/(μg)) ln (1+(m_0 /M)) since a≥0 for t≤t_1 , the max. v is reached at t_1 : v_(max) =v_1 =uλ ln(1+(m_0 /M))−((μgm_0 )/q) (ds/dt)=uλ ln (M_0 /(M_0 −qt))−μgt ∫_0 ^s ds=∫_0 ^t (uλ ln (M_0 /(M_0 −qt))−μgt)dt s(t)=((uλ)/q)[M_0 ln (M_0 −qt)+qtln ((M_0 /(M_0 −qt)))+qt]_0 ^t −((μgt^2 )/2) s(t)=((uλ)/q)[qt−(M_0 −qt)ln ((M_0 /(M_0 −qt)))]−((μgt^2 )/2) s(t)=uλ[t−((M_0 /q)−t)ln ((M_0 /(M_0 −qt)))]−((μgt^2 )/2) at t=t_1 : s_1 =((uλ)/q)[m_0 −Mln ((M_0 /M))]−((μgm_0 ^2 )/(2q^2 )) distance covered in t_1 ≤t≤t_2 : Δs_2 =(v_1 ^2 /(2μg))=(1/(2μg))[uλ ln (M_0 /M)−((μgm_0 )/q)]^2 total distance: s_(max) =s_2 =s_1 +Δs_2 ⇒s_(max) =((uλ)/q)[m_0 −M ln (1+(m_0 /M))]−((μgm_0 ^2 )/(2q^2 ))+(1/(2μg))[uλ ln(1+ (m_0 /M))−((μgm_0 )/q)]^2](Q43203.png)
$${let}\:{m}_{\mathrm{0}} ={mass}\:{of}\:{fuel}\:{at}\:{t}=\mathrm{0} \\ $$$$ \\ $$$${let}'{s}\:{say}\:{at}\:{t}={t}_{\mathrm{1}} \:{tank}\:{is}\:{empty}. \\ $$$${and}\:{it}\:{stops}\:{at}\:{t}={t}_{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant{t}\leqslant{t}_{\mathrm{1}} :\:{motion}\:{with}\:{variable}\:{mass}\:{M}+{m} \\ $$$${t}_{\mathrm{1}} \leqslant{t}\leqslant{t}_{\mathrm{2}} :\:{motion}\:{with}\:{constant}\:{mass}\:{M} \\ $$$$ \\ $$$${in}\:{following}\:{it}\:{is}\:{assumed}\:{that}\:{the} \\ $$$${friction}\:{is}\:{so}\:{small}\:{as}\:{well}\:{as}\:{u}\:{and} \\ $$$${q}\:{are}\:{so}\:{large}\:{that}\:{the}\:{toy}\:{starts}\:{to} \\ $$$${move}\:{at}\:{t}=\mathrm{0},\:{see}\:{condition}\:\left({I}\right). \\ $$$$ \\ $$$$\left({M}+{m}\right){g}−{N}−{u}\:\mathrm{sin}\:\theta\:\frac{{d}\left({M}+{m}\right)}{{dt}}=\mathrm{0} \\ $$$$\Rightarrow{N}=\left({M}+{m}\right){g}+{uq}\:\mathrm{sin}\:\theta \\ $$$$−{N}\mu−{u}\:\mathrm{cos}\:\theta\:\frac{{d}\left({M}+{m}\right)}{{dt}}=\left({M}+{m}\right)\frac{{dv}}{{dt}} \\ $$$$\Rightarrow−\left({M}+{m}\right)\mu{g}+\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right){uq}=\left({M}+{m}\right)\frac{{dv}}{{dt}} \\ $$$$\Rightarrow\left({M}+{m}\right)\left(\mu{g}+\frac{{dv}}{{dt}}\right)={uq}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$${m}={m}_{\mathrm{0}} −{qt} \\ $$$$\Rightarrow\left({M}+{m}_{\mathrm{0}} −{qt}\right)\left(\mu{g}+\frac{{dv}}{{dt}}\right)={uq}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\frac{{dv}}{{dt}}=\frac{{uq}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right)}{{M}+{m}_{\mathrm{0}} −{qt}}−\mu{g} \\ $$$${let}\:{M}_{\mathrm{0}} ={M}+{m}_{\mathrm{0}} ,\:\lambda=\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}=\frac{{dv}}{{dt}}=\frac{{uq}\lambda}{{M}_{\mathrm{0}} −{qt}}−\mu{g} \\ $$$${so}\:{that}\:{the}\:{toy}\:{starts}\:{to}\:{move}\:{at}\:{t}=\mathrm{0}, \\ $$$$\frac{{uq}\lambda}{{M}_{\mathrm{0}} }−\mu{g}\geqslant\mathrm{0} \\ $$$$\Rightarrow{uq}\geqslant\frac{\mu{gM}_{\mathrm{0}} }{\lambda}=\frac{\mu{g}\left({M}+{m}_{\mathrm{0}} \right)}{\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta}\:\:...\left({I}\right) \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{{v}} {dv}=\int_{\mathrm{0}} ^{{t}} \left(\frac{{uq}\lambda}{{M}_{\mathrm{0}} −{qt}}−\mu{g}\right){dt} \\ $$$$\Rightarrow{v}=\left[−{u}\lambda\:\mathrm{ln}\:\left({M}_{\mathrm{0}} −{qt}\right)−\mu{gt}\right]_{\mathrm{0}} ^{{t}} \\ $$$$\Rightarrow{v}\left({t}\right)={u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}−\mu{gt} \\ $$$${this}\:{is}\:{valid}\:{for}\:{t}\leqslant{t}_{\mathrm{1}} =\frac{{m}_{\mathrm{0}} }{{q}}={moment}\:{when}\:{tank}\:{is}\:{empty} \\ $$$${v}_{\mathrm{1}} ={v}\left({t}_{\mathrm{1}} \right)={u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}}−\frac{\mu{gm}_{\mathrm{0}} }{{q}} \\ $$$$ \\ $$$${for}\:{t}>{t}_{\mathrm{1}} : \\ $$$$−\mu{Mg}={M}\frac{{dv}}{{dt}} \\ $$$$\Rightarrow\frac{{dv}}{{dt}}=−\mu{g} \\ $$$$\int_{{v}_{\mathrm{1}} } ^{{v}} {dv}=−\int_{{t}_{\mathrm{1}} } ^{{t}} \mu{gdt} \\ $$$${v}\left({t}\right)−{v}_{\mathrm{1}} =−\mu{g}\left({t}−{t}_{\mathrm{1}} \right) \\ $$$$\Rightarrow{v}\left({t}\right)={v}_{\mathrm{1}} −\mu{g}\left({t}−{t}_{\mathrm{1}} \right) \\ $$$${at}\:{t}={t}_{\mathrm{2}} :\:{v}=\mathrm{0} \\ $$$${u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}}−\frac{\mu{gm}_{\mathrm{0}} }{{q}}−\mu{g}\left({t}_{\mathrm{2}} −\frac{{m}_{\mathrm{0}} }{{q}}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{2}} =\frac{{u}\lambda}{\mu{g}}\:\mathrm{ln}\:\left(\mathrm{1}+\frac{{m}_{\mathrm{0}} }{{M}}\right) \\ $$$$ \\ $$$${since}\:{a}\geqslant\mathrm{0}\:{for}\:{t}\leqslant{t}_{\mathrm{1}} ,\:{the}\:{max}.\:{v}\:{is}\:{reached}\:{at}\:{t}_{\mathrm{1}} : \\ $$$${v}_{{max}} ={v}_{\mathrm{1}} ={u}\lambda\:\mathrm{ln}\left(\mathrm{1}+\frac{{m}_{\mathrm{0}} }{{M}}\right)−\frac{\mu{gm}_{\mathrm{0}} }{{q}} \\ $$$$ \\ $$$$\frac{{ds}}{{dt}}={u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}−\mu{gt} \\ $$$$\int_{\mathrm{0}} ^{{s}} {ds}=\int_{\mathrm{0}} ^{{t}} \left({u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}−\mu{gt}\right){dt} \\ $$$${s}\left({t}\right)=\frac{{u}\lambda}{{q}}\left[{M}_{\mathrm{0}} \mathrm{ln}\:\left({M}_{\mathrm{0}} −{qt}\right)+{qt}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right)+{qt}\right]_{\mathrm{0}} ^{{t}} −\frac{\mu{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${s}\left({t}\right)=\frac{{u}\lambda}{{q}}\left[{qt}−\left({M}_{\mathrm{0}} −{qt}\right)\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right)\right]−\frac{\mu{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${s}\left({t}\right)={u}\lambda\left[{t}−\left(\frac{{M}_{\mathrm{0}} }{{q}}−{t}\right)\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}_{\mathrm{0}} −{qt}}\right)\right]−\frac{\mu{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${at}\:{t}={t}_{\mathrm{1}} : \\ $$$${s}_{\mathrm{1}} =\frac{{u}\lambda}{{q}}\left[{m}_{\mathrm{0}} −{M}\mathrm{ln}\:\left(\frac{{M}_{\mathrm{0}} }{{M}}\right)\right]−\frac{\mu{gm}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}{q}^{\mathrm{2}} } \\ $$$${distance}\:{covered}\:{in}\:{t}_{\mathrm{1}} \leqslant{t}\leqslant{t}_{\mathrm{2}} : \\ $$$$\Delta{s}_{\mathrm{2}} =\frac{{v}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\mu{g}}=\frac{\mathrm{1}}{\mathrm{2}\mu{g}}\left[{u}\lambda\:\mathrm{ln}\:\frac{{M}_{\mathrm{0}} }{{M}}−\frac{\mu{gm}_{\mathrm{0}} }{{q}}\right]^{\mathrm{2}} \\ $$$$ \\ $$$${total}\:{distance}: \\ $$$${s}_{{max}} ={s}_{\mathrm{2}} ={s}_{\mathrm{1}} +\Delta{s}_{\mathrm{2}} \\ $$$$\Rightarrow{s}_{{max}} =\frac{{u}\lambda}{{q}}\left[{m}_{\mathrm{0}} −{M}\:\mathrm{ln}\:\left(\mathrm{1}+\frac{{m}_{\mathrm{0}} }{{M}}\right)\right]−\frac{\mu{gm}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\mu{g}}\left[{u}\lambda\:\mathrm{ln}\left(\mathrm{1}+\:\frac{{m}_{\mathrm{0}} }{{M}}\right)−\frac{\mu{gm}_{\mathrm{0}} }{{q}}\right]^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 08/Sep/18
$${Thanks}\:{Sir},\:{v}_{{max}} \:{matches},\:{rest} \\ $$$${should}\:{agree}\:{too}. \\ $$