Question Number 43192 by Raj Singh last updated on 08/Sep/18
Commented by Rauny last updated on 09/Sep/18
$$\mathrm{cosec}\:{x}+\mathrm{sec}\:{x}=\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}}=\mathrm{2} \\ $$$$\mathrm{cos}\:{x}+\mathrm{sin}\:{x}=\mathrm{2sin}\:{x}\mathrm{cos}\:{x} \\ $$$${A}={B}\Rightarrow{A}^{\mathrm{2}} ={B}^{\mathrm{2}} , \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}=\mathrm{4sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{way}\:\forall{x}:\:\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}=\mathrm{1} \\ $$$${viz}.\:\mathrm{2sin}\:{x}\mathrm{cos}\:{x}+\mathrm{1}=\mathrm{4sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{let}\:\mathrm{sin}\:{x}\mathrm{cos}\:{x}={X}, \\ $$$$\mathrm{4}{X}^{\mathrm{2}} −\mathrm{2}{X}−\mathrm{1}=\mathrm{0} \\ $$$${X}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}}=\mathrm{sin}\:{x}\mathrm{cos}\:{x} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$=\mathrm{sin}^{\mathrm{2}} \:{x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}\right)\:\because\mathrm{cos}^{\mathrm{2}} \:{x}=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$−\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}−\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{8}}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{sin}^{\mathrm{2}} \:{x}={S}, \\ $$$${S}^{\mathrm{2}} −{S}+\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{8}}=−\mathrm{0}=\mathrm{0} \\ $$$${S}=\frac{\mathrm{1}+\sqrt{\frac{\mathrm{5}\mp\sqrt{\mathrm{5}}}{\mathrm{8}}}}{\mathrm{2}}\:\mathrm{or}\:\frac{\mathrm{1}−\sqrt{\frac{\mathrm{5}\mp\sqrt{\mathrm{5}}}{\mathrm{8}}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}\right)\:\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}\right) \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}\right)\:\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}\right) \\ $$$$\therefore\boldsymbol{\mathrm{cosec}}\:\boldsymbol{{x}}=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}}\:\mathrm{or}\:\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}} \\ $$$$\mathrm{or}\:\frac{\mathrm{2}}{\mathrm{1}−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}}\:\mathrm{or}\:\frac{\mathrm{2}}{\mathrm{1}−\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}} \\ $$$$\mathrm{or}\:\frac{−\mathrm{2}}{\mathrm{1}+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}}\:\mathrm{or}\:\frac{−\mathrm{2}}{\mathrm{1}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}} \\ $$$$\mathrm{or}\:\frac{−\mathrm{2}}{\mathrm{1}−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}}}}\:\mathrm{or}\:\frac{−\mathrm{2}}{\mathrm{1}−\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{8}}}} \\ $$$$\blacksquare \\ $$$$\mathrm{omg}.. \\ $$
Commented by Rauny last updated on 10/Sep/18
$$ \\ $$$$\mathrm{I}\:\mathrm{made}\:\mathrm{so}\:\mathrm{many}\:\mathrm{mistakes}..\: \\ $$$${the}\:{real}\:{sollution}:\:\mathrm{cosec}\:{x}+\mathrm{sec}\:{x}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}{i}}, \\ $$$$\mathrm{cosec}\:{x}=\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}\right)\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}{i}}}{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\left(\mathrm{1}−\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}\right)\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}{i}} \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{to}\:\mathrm{sleep}\:\mathrm{now}.\:\mathrm{sorry}! \\ $$
Commented by Rauny last updated on 14/Sep/18
![REALLY EXCELLENT SOLLUTION: cosec x+sec x=2 sin x+cos x=2sin xcos x sin x=((e^(ix) −e^(−ix) )/(2i)), cos x=((e^(ix) +e^(−ix) )/2) And e^(ix) :=E Then ((E−E^(−1) )/(2i))+((E+E^(−1) )/2)=(((E−E^(−1) )(E+E^(−1) ))/(2i)) ⇒((E−E^(−1) +iE+iE^(−1) )/(2i))=((E^2 −E^(−2) )/(2i)) (1+i)E−(1−i)E^(−1) =E^2 −E^(−2) E^2 −(1/E^2 )−(1+i)E+((1−i)/E)=0 E^2 +2i−(1/E^2 )−E−Ei+(1/E)−(1/E)i−2i=0 (E+(1/E)i)^2 −(E+(1/E)i)−(Ei−(1/E))−2i=0 ⇒(E+(1/E)i)^2 −(E+(1/E)i)−(Ei+(1/E)i^2 )−2i=0 ⇒(E+(1/E)i)^2 −(E+(1/E)i)−(E+(1/E)i)i−2i=0 E+(1/E)i:=X, X^2 −X−Xi−2i=0 X^2 −(1+i)X−2i=0 X=((1±(√(10i))+i)/2)=E+(1/E)i E^2 +i=((1±(√(10i))+i)/2)E E^2 −((1±(√(10i))+i)/2)E+i=0 E=(1/2)(−((1±(√(10i))+i)/2)+(√(((±(1+(√(10i))+i)(√(10i)))/4)−(7/2)i)) or (1/2)(−((1±(√(10i))+i)/2)−(√(((±(1+(√(10i))+i)(√(10i)))/4)−(7/2)i)) =e^(ix) 1+i:=j, (√(10i)):=k e^(ix) =(1/2)(−((j±k)/2)+(√(±((j+k)/4)k−(7/2)i))) or (1/2)(−((j±k)/2)−(√(±((j+k)/4)k−(7/2)i))) Then sin x=((e^(ix) −e^(−ix) )/(2i)) =(1/(2i))[−((j±k)/4)+(1/2)(√(±((j+k)/4)k−(7/2)i))−{−(j±k)+2(√(±((j+k)/4)k−(7/2)i))}] or (1/(2i))[−((j±k)/4)−(1/2)(√(±((j+k)/4)k−(7/2)i))−{−(j±k)−2(√(±((j+k)/4)k−(7/2)i))}] =(1/(2i)){(3/4)(j±k)−(3/4)(√(±(j+k)k−14i))} or (1/(2i)){(3/4)(j±k)+(3/4)(√(±(j+k)k−14i))} cosec x=(1/(sin x)) ∴cosec x+sec x=2∧1+i=j∧(√(10i))=k ⇒cosec x=((3i)/2){(j±k)+(√(±(j+k)k−14i))} or ((3i)/2){(j±k)−(√(±(j+k)k−14i))} Q.E.D.](Q43653.png)
$${REALLY}\:\:{EXCELLENT}\:{SOLLUTION}: \\ $$$$\mathrm{cosec}\:{x}+\mathrm{sec}\:{x}=\mathrm{2} \\ $$$$\mathrm{sin}\:{x}+\mathrm{cos}\:{x}=\mathrm{2sin}\:{x}\mathrm{cos}\:{x} \\ $$$$\mathrm{sin}\:{x}=\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}},\:\mathrm{cos}\:{x}=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}} \\ $$$$\mathrm{And}\:{e}^{{ix}} :={E} \\ $$$$\mathrm{Then}\:\frac{{E}−{E}^{−\mathrm{1}} }{\mathrm{2}{i}}+\frac{{E}+{E}^{−\mathrm{1}} }{\mathrm{2}}=\frac{\left({E}−{E}^{−\mathrm{1}} \right)\left({E}+{E}^{−\mathrm{1}} \right)}{\mathrm{2}{i}} \\ $$$$\Rightarrow\frac{{E}−{E}^{−\mathrm{1}} +{iE}+{iE}^{−\mathrm{1}} }{\mathrm{2}{i}}=\frac{{E}^{\mathrm{2}} −{E}^{−\mathrm{2}} }{\mathrm{2}{i}} \\ $$$$\left(\mathrm{1}+{i}\right){E}−\left(\mathrm{1}−{i}\right){E}^{−\mathrm{1}} ={E}^{\mathrm{2}} −{E}^{−\mathrm{2}} \\ $$$${E}^{\mathrm{2}} −\frac{\mathrm{1}}{{E}^{\mathrm{2}} }−\left(\mathrm{1}+{i}\right){E}+\frac{\mathrm{1}−{i}}{{E}}=\mathrm{0} \\ $$$${E}^{\mathrm{2}} +\mathrm{2}{i}−\frac{\mathrm{1}}{{E}^{\mathrm{2}} }−{E}−{Ei}+\frac{\mathrm{1}}{{E}}−\frac{\mathrm{1}}{{E}}{i}−\mathrm{2}{i}=\mathrm{0} \\ $$$$\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)^{\mathrm{2}} −\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)−\left({Ei}−\frac{\mathrm{1}}{{E}}\right)−\mathrm{2}{i}=\mathrm{0} \\ $$$$\Rightarrow\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)^{\mathrm{2}} −\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)−\left({Ei}+\frac{\mathrm{1}}{{E}}{i}^{\mathrm{2}} \right)−\mathrm{2}{i}=\mathrm{0} \\ $$$$\Rightarrow\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)^{\mathrm{2}} −\left({E}+\frac{\mathrm{1}}{{E}}{i}\right)−\left({E}+\frac{\mathrm{1}}{{E}}{i}\right){i}−\mathrm{2}{i}=\mathrm{0} \\ $$$${E}+\frac{\mathrm{1}}{{E}}{i}:={X}, \\ $$$${X}^{\mathrm{2}} −{X}−{Xi}−\mathrm{2}{i}=\mathrm{0} \\ $$$${X}^{\mathrm{2}} −\left(\mathrm{1}+{i}\right){X}−\mathrm{2}{i}=\mathrm{0} \\ $$$${X}=\frac{\mathrm{1}\pm\sqrt{\mathrm{10}{i}}+{i}}{\mathrm{2}}={E}+\frac{\mathrm{1}}{{E}}{i} \\ $$$${E}^{\mathrm{2}} +{i}=\frac{\mathrm{1}\pm\sqrt{\mathrm{10}{i}}+{i}}{\mathrm{2}}{E} \\ $$$${E}^{\mathrm{2}} −\frac{\mathrm{1}\pm\sqrt{\mathrm{10}{i}}+{i}}{\mathrm{2}}{E}+{i}=\mathrm{0} \\ $$$${E}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}\pm\sqrt{\mathrm{10}{i}}+{i}}{\mathrm{2}}+\sqrt{\frac{\pm\left(\mathrm{1}+\sqrt{\mathrm{10}{i}}+{i}\right)\sqrt{\mathrm{10}{i}}}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right. \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}\pm\sqrt{\mathrm{10}{i}}+{i}}{\mathrm{2}}−\sqrt{\frac{\pm\left(\mathrm{1}+\sqrt{\mathrm{10}{i}}+{i}\right)\sqrt{\mathrm{10}{i}}}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right. \\ $$$$={e}^{{ix}} \\ $$$$\mathrm{1}+{i}:={j},\:\sqrt{\mathrm{10}{i}}:={k} \\ $$$${e}^{{ix}} =\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{{j}\pm{k}}{\mathrm{2}}+\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right) \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{{j}\pm{k}}{\mathrm{2}}−\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right) \\ $$$$\mathrm{Then}\:\mathrm{sin}\:{x}=\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left[−\frac{{j}\pm{k}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}−\left\{−\left({j}\pm{k}\right)+\mathrm{2}\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right\}\right] \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left[−\frac{{j}\pm{k}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}−\left\{−\left({j}\pm{k}\right)−\mathrm{2}\sqrt{\pm\frac{{j}+{k}}{\mathrm{4}}{k}−\frac{\mathrm{7}}{\mathrm{2}}{i}}\right\}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\frac{\mathrm{3}}{\mathrm{4}}\left({j}\pm{k}\right)−\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\pm\left({j}+{k}\right){k}−\mathrm{14}{i}}\right\} \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\frac{\mathrm{3}}{\mathrm{4}}\left({j}\pm{k}\right)+\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\pm\left({j}+{k}\right){k}−\mathrm{14}{i}}\right\} \\ $$$$\mathrm{cosec}\:{x}=\frac{\mathrm{1}}{\mathrm{sin}\:{x}} \\ $$$$\therefore\mathrm{cosec}\:{x}+\mathrm{sec}\:{x}=\mathrm{2}\wedge\mathrm{1}+{i}={j}\wedge\sqrt{\mathrm{10}{i}}={k} \\ $$$$\Rightarrow\mathrm{cosec}\:{x}=\frac{\mathrm{3}{i}}{\mathrm{2}}\left\{\left({j}\pm{k}\right)+\sqrt{\pm\left({j}+{k}\right){k}−\mathrm{14}{i}}\right\} \\ $$$$\mathrm{or}\:\frac{\mathrm{3}{i}}{\mathrm{2}}\left\{\left({j}\pm{k}\right)−\sqrt{\pm\left({j}+{k}\right){k}−\mathrm{14}{i}}\right\} \\ $$$$\mathrm{Q}.\mathrm{E}.\mathrm{D}. \\ $$
Commented by Rauny last updated on 13/Sep/18
$$\mathrm{p}.\mathrm{s}.\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{that}\:\mathrm{for}\:\mathrm{50}\:\mathrm{minutes}.\:\mathrm{lol} \\ $$
Commented by rahul 19 last updated on 13/Sep/18
My God! ����������
Commented by Rauny last updated on 14/Sep/18
$$\left.:\right) \\ $$
Answered by alex041103 last updated on 08/Sep/18
$${let}\:{cosec}\:\phi={t}=\frac{\mathrm{1}}{{sin}\:\phi}>\mathrm{1} \\ $$$$\Rightarrow{sec}\:\phi=\frac{\mathrm{1}}{{cos}\:\phi}=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}=\frac{{t}}{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\Rightarrow{t}+\frac{{t}}{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{2} \\ $$$$\frac{{t}}{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{2}−{t} \\ $$$$\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}=\mathrm{4}+{t}^{\mathrm{2}} −\mathrm{4}{t}\: \\ $$$${if}\:{t}\neq\mathrm{1}\left({t}=\mathrm{1}\:{is}\:{not}\:{a}\:{solution}\right) \\ $$$$\Rightarrow{t}^{\mathrm{2}} =\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:={t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} +\mathrm{4}{t}^{\mathrm{2}} \:−\:{t}^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{4} \\ $$$$\Rightarrow{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{the}\:{real}\:{solutions}\:{are}: \\ $$$${t}_{\mathrm{1}} =\mathrm{1}−\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$$${t}_{\mathrm{2}} =\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$$${The}\:{two}\:{solutions}\:{are}\:{t}_{\mathrm{1},\mathrm{2}} \in\mathbb{R}−\left(−\mathrm{1};\mathrm{1}\right) \\ $$$$\Rightarrow\phi_{\mathrm{1};\mathrm{2}} \:{exists} \\ $$$$\Rightarrow{cosec}\phi=\mathrm{1}−\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}};\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$
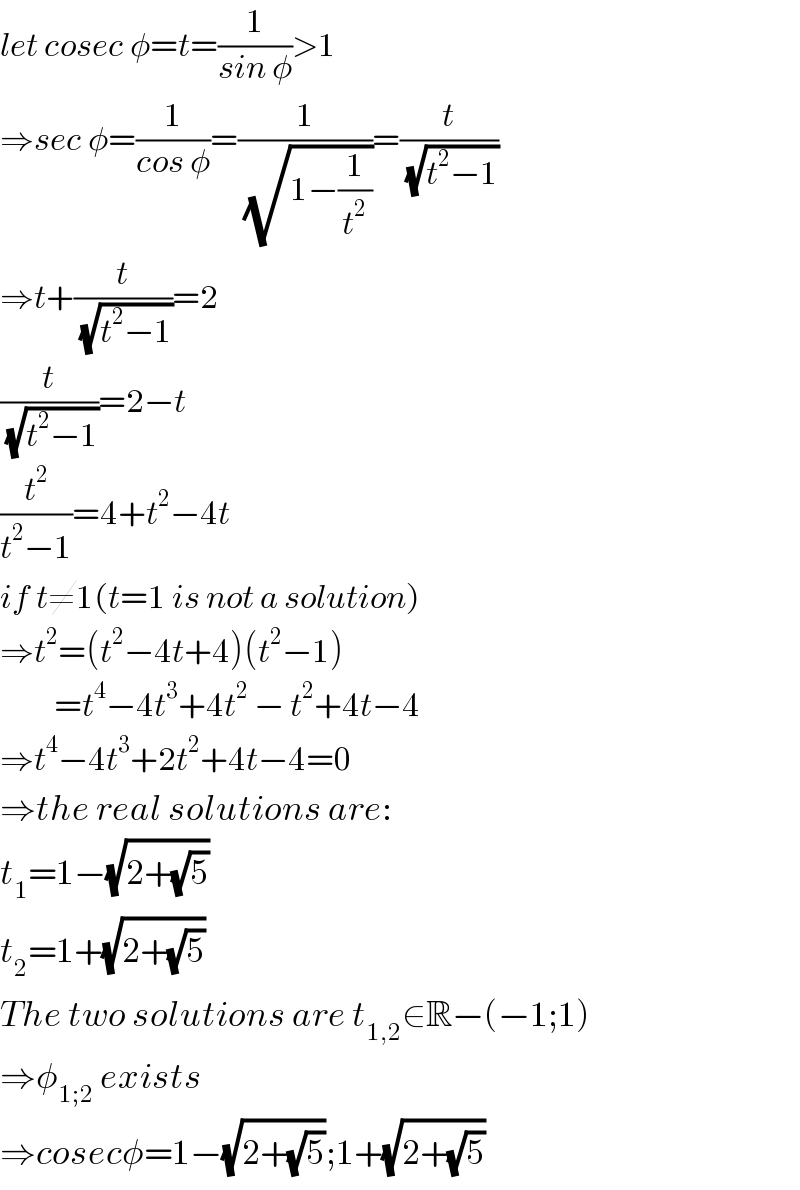
Commented by malwaan last updated on 09/Sep/18
$$\mathrm{thank}\:\mathrm{you} \\ $$