
Question and Answers Forum
Question Number 43252 by ajfour last updated on 08/Sep/18

Commented by MJS last updated on 08/Sep/18
![circle x^2 +y^2 =1 y=(√(1−x^2 )) parabola x=ay^2 −1 y=(√(a(x+1))); a>0 circle ∩ parabola 1−x^2 =a(x+1) x^2 +ax+(a−1)=0 x_1 =−1 [trivial] x_2 =1−a y_2 =(√(a(2−a))) ((area above parabola)/(area below parabola))=2 ((∫_(−1) ^(1−a) (√(1−x^2 ))dx−∫_(−1) ^(1−a) (√(a(x+1)))dx)/(∫_(−1) ^(1−a) (√(a(x+1)))dx+∫_(1−a) ^1 (√(1−x^2 ))dx))=2 (3/2)(arcsin(1−a)+(1−a)(√(a(2−a))))−2(√(a(2−a)^3 ))−(π/4)=0 a≈.0802770 x_2 ≈.919723 y_2 ≈.392568 α=2arctan (y_2 /x_2 ) ≈46.2288°](Q43254.png)
Commented by ajfour last updated on 09/Sep/18

Answered by MrW3 last updated on 08/Sep/18
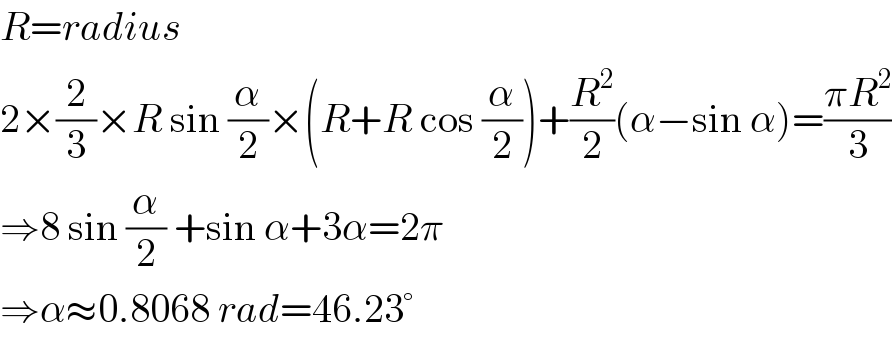
Commented by MrW3 last updated on 09/Sep/18

Commented by MrW3 last updated on 09/Sep/18
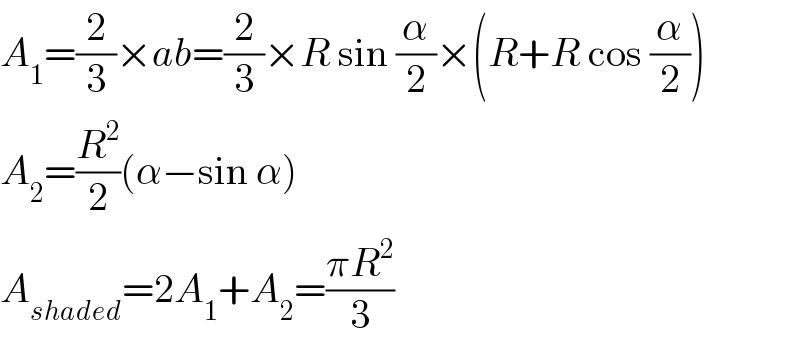
Commented by ajfour last updated on 09/Sep/18
Commented by MrW3 last updated on 09/Sep/18
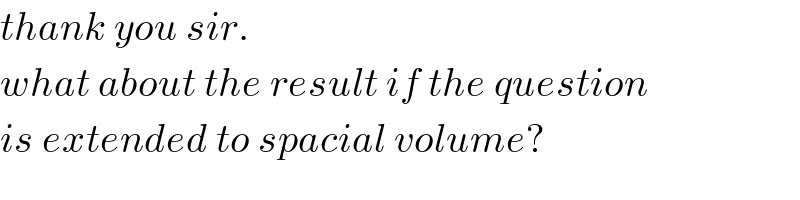
Commented by MrW3 last updated on 09/Sep/18
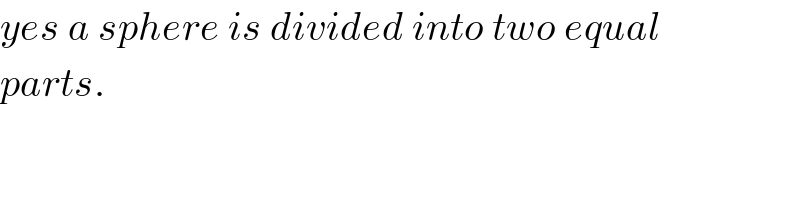
Commented by ajfour last updated on 09/Sep/18
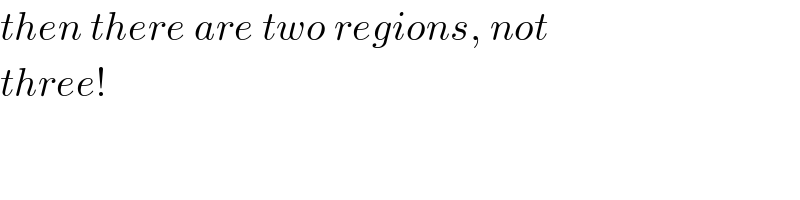
Answered by ajfour last updated on 09/Sep/18
![3D extension: sphere: r^2 +(z−R)^2 =R^2 paraboloid : z = Ar^2 let A(a, Aa^2 ) ⇒ a^2 +(Aa^2 −R)^2 =R^2 ⇒ Aa^2 =R+(√(R^2 −a^2 )) .....(i) or ((Aa^2 )/R)=1+(√(1−((a/R))^2 )) ...(i)^∗ ∫_0 ^( a) (z_(sphere) −z_(para) )(2πrdr)=((2πR^3 )/3) ⇒∫_0 ^( a) [R+(√(R^2 −r^2 ))−Ar^2 ]rdr = (R^3 /3) ....(ii) ((a^2 R)/2)−(((R^2 −a^2 )^(3/2) )/3)+(R^3 /3)−((Aa^4 )/4)=(R^3 /3) (a/R)=x = sin (α/2) ⇒ 6x^2 −4(1−x^2 )^(3/2) = 3x^2 (1+(√(1−x^2 )) ) ⇒ 6sin^2 (α/2)−4cos^3 (α/2)=3(sin^2 (α/2))(1+cos (α/2)) let cos (α/2) = p ⇒ 6(1−p^2 )−4p^3 =3(1−p^2 )(1+p) ⇒ p^3 +3p^2 +3p+1 = 4 ⇒ (p+1)^3 =4 p = (4)^(1/3) −1 𝛂 = 2cos^(−1) p = 2cos^(−1) ((4)^(1/3) −1) ≈ 108.0545 .](Q43314.png)
Commented by MrW3 last updated on 09/Sep/18
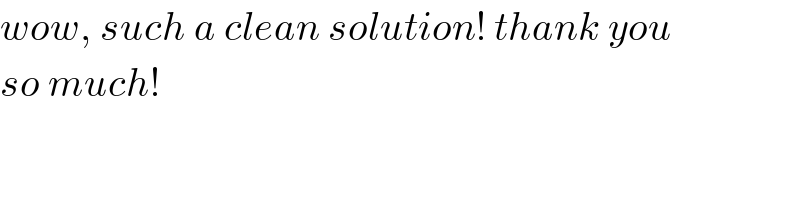
Answered by MrW3 last updated on 09/Sep/18
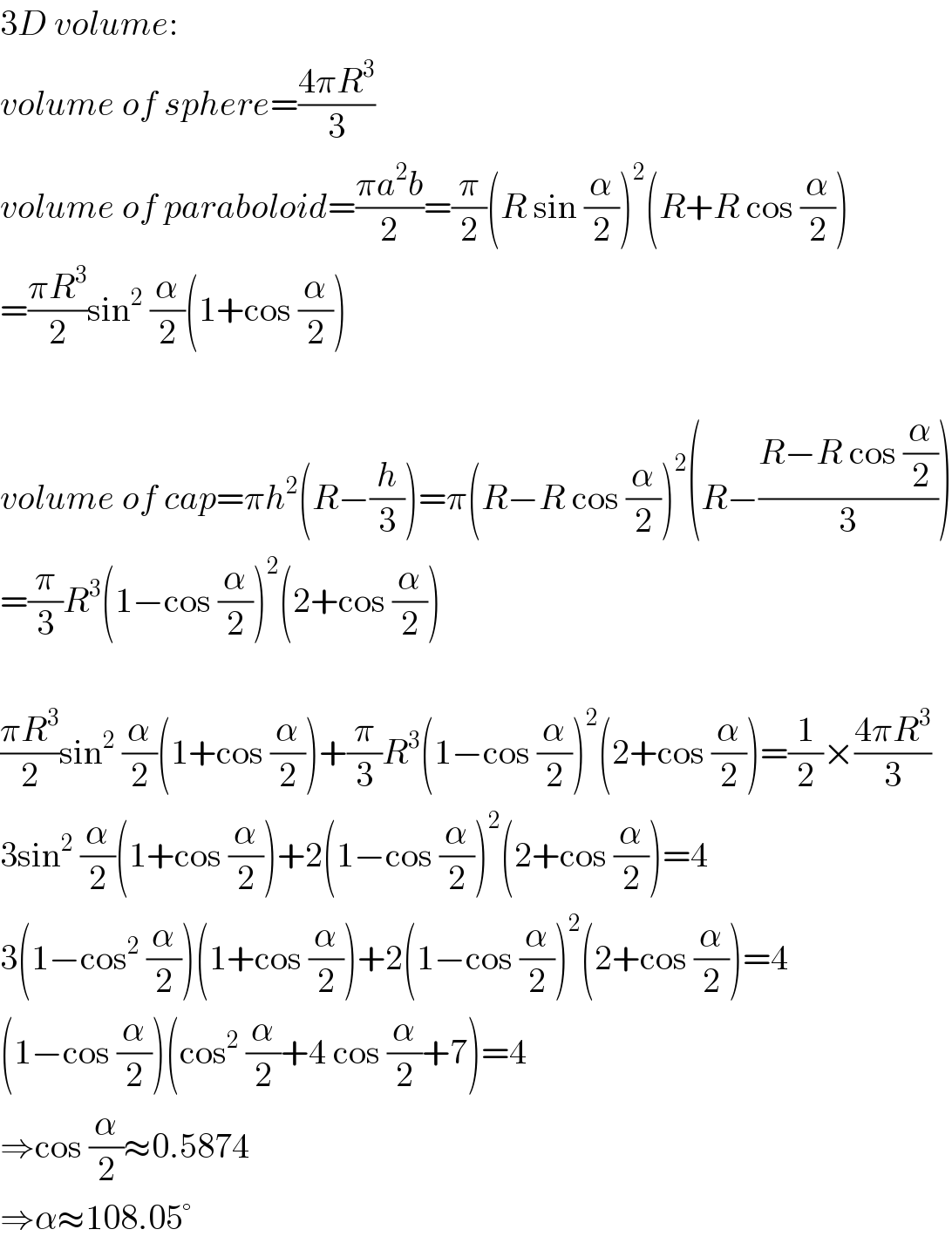
Commented by ajfour last updated on 09/Sep/18

