Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 43363 by rahul 19 last updated on 10/Sep/18

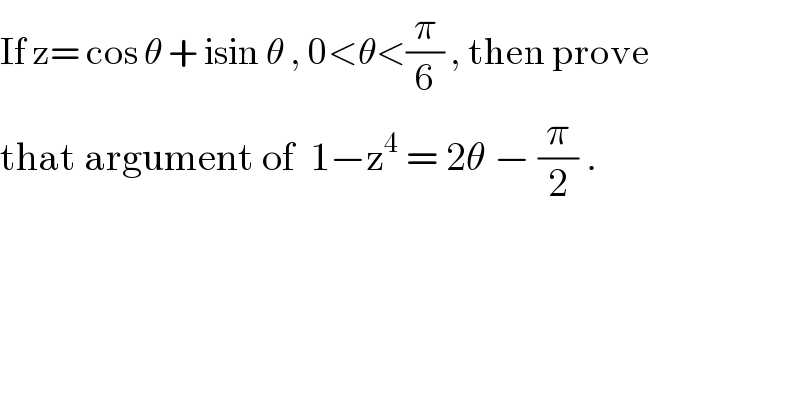
If z= cos θ + isin θ , 0<θ<(π/6) , then prove that argument of 1−z^4 = 2θ − (π/2) .

$$\mathrm{If}\:\mathrm{z}=\:\mathrm{cos}\:\theta\:+\:\mathrm{isin}\:\theta\:,\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{6}}\:,\:\mathrm{then}\:\mathrm{prove} \\ $$ $$\mathrm{that}\:\mathrm{argument}\:\mathrm{of}\:\:\mathrm{1}−\mathrm{z}^{\mathrm{4}} \:=\:\mathrm{2}\theta\:−\:\frac{\pi}{\mathrm{2}}\:. \\ $$

Commented bymaxmathsup by imad last updated on 10/Sep/18

we have z =e^(iθ) ⇒1−z^4 =1−e^(4iθ) =1−cos(4θ)−isin(4θ) =2 sin^2 (2θ) −2isin(2θ)cos(2θ) =−2isin(2θ){cos(2θ) +isin(2θ)} =2 sin(2θ)(−i) e^(i(2θ)) we have 0<2θ<(π/3) ⇒sin(2θ)>0 ⇒∣1−z^4 ∣ =2 sin(2θ) and arg(1−z^4 ) ≡arg(−i) +2θ [2π] ⇒arg(1−z^4 )≡ −(π/2) +2θ[2π] .

$${we}\:{have}\:{z}\:={e}^{{i}\theta} \:\Rightarrow\mathrm{1}−{z}^{\mathrm{4}} \:=\mathrm{1}−{e}^{\mathrm{4}{i}\theta} \:\:\:=\mathrm{1}−{cos}\left(\mathrm{4}\theta\right)−{isin}\left(\mathrm{4}\theta\right) \\ $$ $$=\mathrm{2}\:{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right)\:−\mathrm{2}{isin}\left(\mathrm{2}\theta\right){cos}\left(\mathrm{2}\theta\right)\:=−\mathrm{2}{isin}\left(\mathrm{2}\theta\right)\left\{{cos}\left(\mathrm{2}\theta\right)\:+{isin}\left(\mathrm{2}\theta\right)\right\} \\ $$ $$=\mathrm{2}\:{sin}\left(\mathrm{2}\theta\right)\left(−\boldsymbol{{i}}\right)\:\boldsymbol{{e}}^{\boldsymbol{{i}}\left(\mathrm{2}\theta\right)} \:\:{we}\:{have}\:\:\mathrm{0}<\mathrm{2}\theta<\frac{\pi}{\mathrm{3}}\:\Rightarrow{sin}\left(\mathrm{2}\theta\right)>\mathrm{0}\:\Rightarrow\mid\mathrm{1}−{z}^{\mathrm{4}} \mid\:=\mathrm{2}\:{sin}\left(\mathrm{2}\theta\right) \\ $$ $${and}\:\:{arg}\left(\mathrm{1}−{z}^{\mathrm{4}} \right)\:\equiv{arg}\left(−{i}\right)\:+\mathrm{2}\theta\:\:\left[\mathrm{2}\pi\right]\:\Rightarrow{arg}\left(\mathrm{1}−{z}^{\mathrm{4}} \right)\equiv\:−\frac{\pi}{\mathrm{2}}\:+\mathrm{2}\theta\left[\mathrm{2}\pi\right]\:. \\ $$

Answered by ajfour last updated on 10/Sep/18

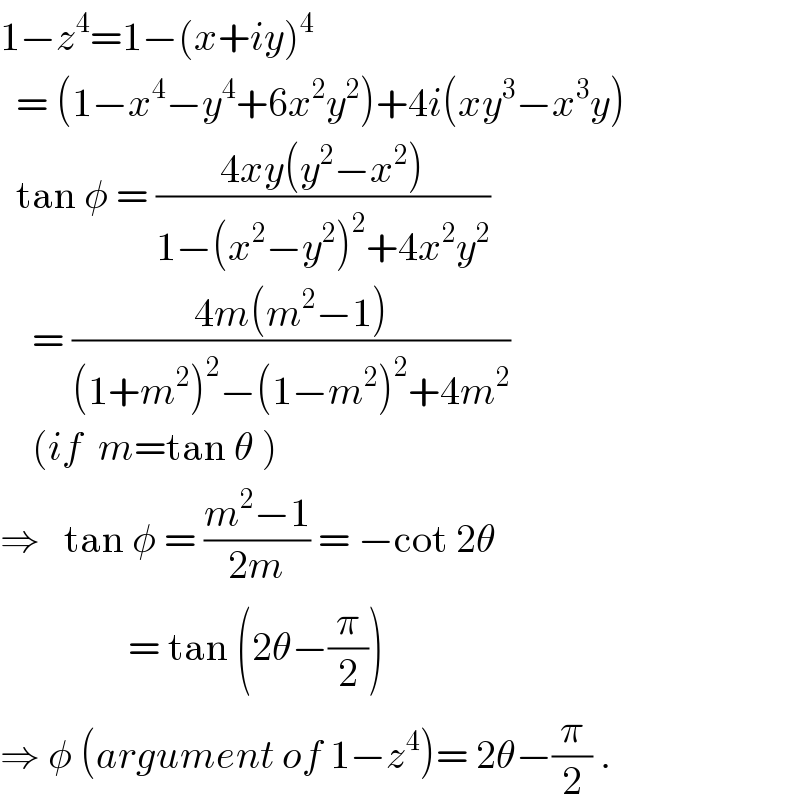
1−z^4 =1−(x+iy)^4 = (1−x^4 −y^4 +6x^2 y^2 )+4i(xy^3 −x^3 y) tan φ = ((4xy(y^2 −x^2 ))/(1−(x^2 −y^2 )^2 +4x^2 y^2 )) = ((4m(m^2 −1))/((1+m^2 )^2 −(1−m^2 )^2 +4m^2 )) (if m=tan θ ) ⇒ tan φ = ((m^2 −1)/(2m)) = −cot 2θ = tan (2θ−(π/2)) ⇒ φ (argument of 1−z^4 )= 2θ−(π/2) .

$$\mathrm{1}−{z}^{\mathrm{4}} =\mathrm{1}−\left({x}+{iy}\right)^{\mathrm{4}} \\ $$ $$\:\:=\:\left(\mathrm{1}−{x}^{\mathrm{4}} −{y}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)+\mathrm{4}{i}\left({xy}^{\mathrm{3}} −{x}^{\mathrm{3}} {y}\right) \\ $$ $$\:\:\mathrm{tan}\:\phi\:=\:\frac{\mathrm{4}{xy}\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}{\mathrm{1}−\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} } \\ $$ $$\:\:\:\:=\:\frac{\mathrm{4}{m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{m}^{\mathrm{2}} } \\ $$ $$\:\:\:\:\left({if}\:\:{m}=\mathrm{tan}\:\theta\:\right) \\ $$ $$\Rightarrow\:\:\:\mathrm{tan}\:\phi\:=\:\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{m}}\:=\:−\mathrm{cot}\:\mathrm{2}\theta \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}\:\left(\mathrm{2}\theta−\frac{\pi}{\mathrm{2}}\right) \\ $$ $$\Rightarrow\:\phi\:\left({argument}\:{of}\:\mathrm{1}−{z}^{\mathrm{4}} \right)=\:\mathrm{2}\theta−\frac{\pi}{\mathrm{2}}\:. \\ $$

Commented byrahul 19 last updated on 10/Sep/18

thanks sir.

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

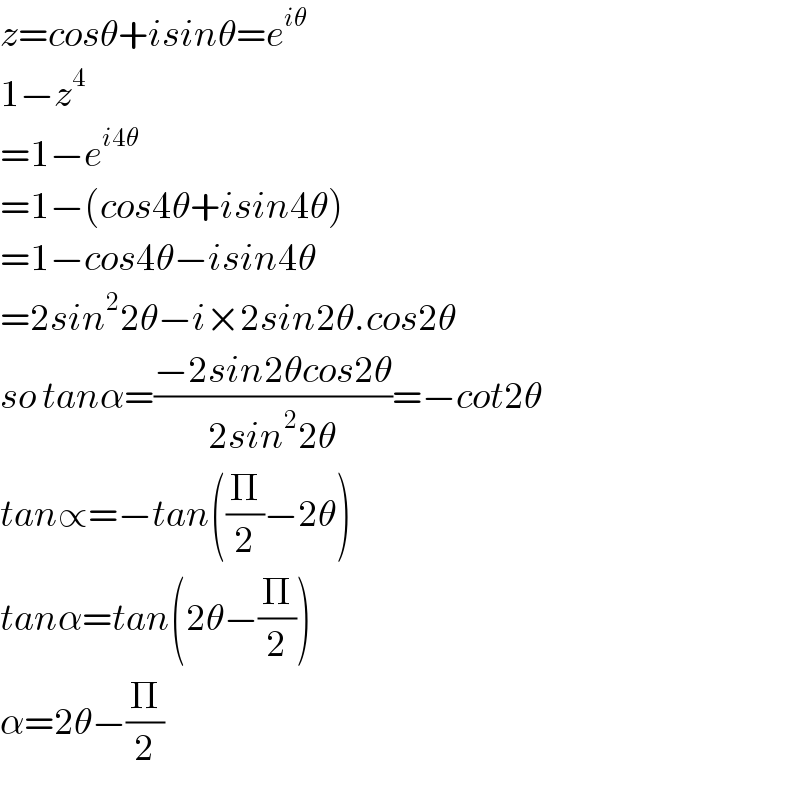
z=cosθ+isinθ=e^(iθ) 1−z^4 =1−e^(i4θ) =1−(cos4θ+isin4θ) =1−cos4θ−isin4θ =2sin^2 2θ−i×2sin2θ.cos2θ so tanα=((−2sin2θcos2θ)/(2sin^2 2θ))=−cot2θ tan∝=−tan((Π/2)−2θ) tanα=tan(2θ−(Π/2)) α=2θ−(Π/2)

$${z}={cos}\theta+{isin}\theta={e}^{{i}\theta} \\ $$ $$\mathrm{1}−{z}^{\mathrm{4}} \\ $$ $$=\mathrm{1}−{e}^{{i}\mathrm{4}\theta} \\ $$ $$=\mathrm{1}−\left({cos}\mathrm{4}\theta+{isin}\mathrm{4}\theta\right) \\ $$ $$=\mathrm{1}−{cos}\mathrm{4}\theta−{isin}\mathrm{4}\theta \\ $$ $$=\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}\theta−{i}×\mathrm{2}{sin}\mathrm{2}\theta.{cos}\mathrm{2}\theta \\ $$ $${so}\:{tan}\alpha=\frac{−\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{2}\theta}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}\theta}=−{cot}\mathrm{2}\theta \\ $$ $${tan}\propto=−{tan}\left(\frac{\Pi}{\mathrm{2}}−\mathrm{2}\theta\right) \\ $$ $${tan}\alpha={tan}\left(\mathrm{2}\theta−\frac{\Pi}{\mathrm{2}}\right) \\ $$ $$\alpha=\mathrm{2}\theta−\frac{\Pi}{\mathrm{2}} \\ $$

Commented byrahul 19 last updated on 10/Sep/18

thanks sir.

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

z=cosθ+isinθ=e^(iθ) 1−z^4 =1−e^(i4θ) =1−(cos4θ+isin4θ) =1−cos4θ−isin4θ =2sin^2 2θ−i×2sin2θ.cos2θ so tanα=((−2sin2θcos2θ)/(2sin^2 2θ))=−cot2θ tan∝=−tan((Π/2)−2θ) tanα=tan(2θ−(Π/2)) α=2θ−(Π/2)

$${z}={cos}\theta+{isin}\theta={e}^{{i}\theta} \\ $$ $$\mathrm{1}−{z}^{\mathrm{4}} \\ $$ $$=\mathrm{1}−{e}^{{i}\mathrm{4}\theta} \\ $$ $$=\mathrm{1}−\left({cos}\mathrm{4}\theta+{isin}\mathrm{4}\theta\right) \\ $$ $$=\mathrm{1}−{cos}\mathrm{4}\theta−{isin}\mathrm{4}\theta \\ $$ $$=\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}\theta−{i}×\mathrm{2}{sin}\mathrm{2}\theta.{cos}\mathrm{2}\theta \\ $$ $${so}\:{tan}\alpha=\frac{−\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{2}\theta}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}\theta}=−{cot}\mathrm{2}\theta \\ $$ $${tan}\propto=−{tan}\left(\frac{\Pi}{\mathrm{2}}−\mathrm{2}\theta\right) \\ $$ $${tan}\alpha={tan}\left(\mathrm{2}\theta−\frac{\Pi}{\mathrm{2}}\right) \\ $$ $$\alpha=\mathrm{2}\theta−\frac{\Pi}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com