Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 43386 by ajfour last updated on 10/Sep/18

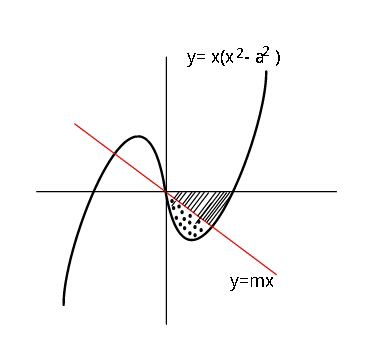
Commented by ajfour last updated on 10/Sep/18

$I f t h e t w o d i f f e r e n t l y s h a d e d$ $a r e a s a r e e q u a l, f i n d s l o p e m o f$ $l i n e, i n t e r m s o f a .$
Commented by Tawa1 last updated on 10/Sep/18

$Sir, please how did you draw the smoth curve using lekh diagram ?$
Commented by ajfour last updated on 10/Sep/18

$q u i c k l y m o v e d f i n g e r l i k e a$ $p a r a b o l a (o n e b r a n c h l o n g, o t h e r$ $s h o r t), (l e k h r e c o g n i s e d i t),$ $c o p i e d i t, f l i p p e d t h e c o p y$ $v e r i c a l t h e n h o r i z o n t a l a n d$ $j o i n e d t h e b r a n c h e n d s o f$ $o r i g i n a l a n d c o p i e d o n e, t h e n$ $g r o u p e d t h e m, t h e n r e s i z e d i t .$
Commented by Tawa1 last updated on 10/Sep/18

$God bless you sir$
	Answered by MrW3 last updated on 10/Sep/18
	$y=x(x^2 −a^2 ) (dy/dx)=3x^2 −a^2 at x=0: tan θ_0 =−a^2 ⇒r sin θ=r cos θ(r^2 cos^2 θ−a^2 ) ⇒r^2 =((tan θ+a^2 )/(cos^2 θ)) A=∫_θ_0 ^(2π) ((r^2 dθ)/2)=(1/2)∫_θ_0 ^(2π) ((tan θ+a^2 )/(cos^2 θ)) dθ =(1/2)∫_θ_0 ^(2π) (tan θ+a^2 ) d(tan θ) =(1/2)[((tan^2 θ)/2)+a^2 tan θ]_θ_0 ^(2π) =(1/2)[−(a^4 /2)+a^4 ]=(a^4 /4) let tan θ_1 =m A_1 =(1/2)[((tan^2 θ)/2)+a^2 tan θ]_θ_1 ^(2π) =(1/2)[−((tan^2 θ_1 )/2)−a^2 tan θ_1 ] =−(1/2)[(m^2 /2)+a^2 m]=(A/2)=(a^4 /8) ⇒2m^2 +4a^2 m+a^4 =0 ⇒m=((−4a^2 ±(√(16a^4 −8a^4 )))/4) = { ((−((2+(√2))/2)a^2 )),((−((2−(√2))/2)a^2 )) :} since ∣θ_1 ∣<∣θ_0 ∣⇒∣m∣=∣tan θ_1 ∣<∣tan θ_0 ∣=a^2 the suitable solution is: m=−((2−(√2))/2)a^2 ≈−0.293a^2$
	$y = x (x^{2} - a^{2})$ $\frac{d y}{d x} = 3 x^{2} - a^{2}$ $a t x = 0 : \tan θ_{0} = - a^{2}$ $\Rightarrow r \sin θ = r \cos θ (r^{2} \cos^{2} θ - a^{2})$ $\Rightarrow r^{2} = \frac{\tan θ + a^{2}}{\cos^{2} θ}$ $A = \int_{θ_{0}}^{2 π} \frac{r^{2} d θ}{2} = \frac{1}{2} \int_{θ_{0}}^{2 π} \frac{\tan θ + a^{2}}{\cos^{2} θ} d θ$ $= \frac{1}{2} \int_{θ_{0}}^{2 π} (\tan θ + a^{2}) d (\tan θ)$ $= \frac{1}{2} {[\frac{\tan^{2} θ}{2} + a^{2} \tan θ]}_{θ_{0}}^{2 π}$ $= \frac{1}{2} [- \frac{a^{4}}{2} + a^{4}] = \frac{a^{4}}{4}$ $l e t \tan θ_{1} = m$ $A_{1} = \frac{1}{2} {[\frac{\tan^{2} θ}{2} + a^{2} \tan θ]}_{θ_{1}}^{2 π}$ $= \frac{1}{2} [- \frac{\tan^{2} θ_{1}}{2} - a^{2} \tan θ_{1}]$ $= - \frac{1}{2} [\frac{m^{2}}{2} + a^{2} m] = \frac{A}{2} = \frac{a^{4}}{8}$ $\Rightarrow 2 m^{2} + 4 a^{2} m + a^{4} = 0$ $\Rightarrow m = \frac{- 4 a^{2} \pm \sqrt{16 a^{4} - 8 a^{4}}}{4}$ $= {\begin{cases} - \frac{2 + \sqrt{2}}{2} a^{2} \\ - \frac{2 - \sqrt{2}}{2} a^{2} \end{cases}$ $s i n c e ∣ θ_{1} ∣<∣ θ_{0} ∣\Rightarrow∣ m ∣=∣ \tan θ_{1} ∣<∣ \tan θ_{0} ∣= a^{2}$ $t h e s u i t a b l e s o l u t i o n i s :$ $m = - \frac{2 - \sqrt{2}}{2} a^{2} \approx - 0.293 a^{2}$
	Commented by ajfour last updated on 10/Sep/18

	$T h a n k s S i r, i g o t t h e s a m e a n s w e r .$
	Answered by ajfour last updated on 10/Sep/18

	$I n t e r s e c t i o n p o i n t s o f l i n e$ $a n d c u r v e :$ $y = m x = x (x^{2} - a^{2})$ $\Rightarrow O (0, 0) a n d P (\sqrt{a^{2} + m}, y_{P})$ $A = - \int_{0}^{a} (x^{3} - a^{2} x) d x = - (\frac{a^{4}}{4} - \frac{a^{4}}{2})$ $\Rightarrow A = \frac{a^{4}}{4}$ $\int_{0}^{\sqrt{a^{2} + m}} (m x - x^{3} + a^{2} x) d x = \frac{a^{4}}{8} (= \frac{A}{2})$ $\Rightarrow \frac{m (a^{2} + m)}{2} - \frac{{(a^{2} + m)}^{2}}{4} + \frac{a^{2} (a^{2} + m)}{2} = \frac{a^{4}}{8}$ $\Rightarrow {(a^{2} + m)}^{2} = \frac{a^{4}}{2}$ $\Rightarrow m = (\frac{1}{\sqrt{2}} - 1) a^{2}$ $s a m e a s m = - (\frac{2 - \sqrt{2}}{2}) a^{2} .$ $[\frac{d y}{d x} ∣_{x = 0} = - a^{2}; s o w e r e j e c t$ $m = - (1 + \frac{1}{\sqrt{2}}) a^{2}] .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18
	$solving mx=x(x^2 −a^2 ) x{m−(x^2 −a^2 }=0 x=0 x^2 −a^2 =m x=±(√(a^2 +m)) y=mx intersect the curve at {−(√(a^2 +m)) ,0,(√(a^2 +m)) } the curve y=x(x^2 −a^2 ) intersect x axis at{−a,0,a} now area of dot shaded+line shaded= ∫_0 ^a x(x^2 −a^2 )dx =∫_0 ^a x^3 −x^ a^2 dx =∣(x^4 /4)−(x^2 /2)×a^2 ∣_0 ^a =(a^4 /4)−(a^4 /2) taking the mod of value of area=(a^4 /4) so dot shaded=(a^4 /8) line shaded=(a^4 /8) area line shaded ∫_0 ^((√(a^2 +m)) ) mx dx+∫_((√(a^2 +m)) ) ^a x(x^2 −a^2 )dx =∣((mx^2 )/2)∣_0 ^((√(a^2 +m)) ) +∣(x^4 /4)−((x^2 a^2 )/2)∣_((√(a^2 +m)) ) ^a =((m(a^2 +m))/2)+{((a^4 /4)−(a^4 /2))−(((a^4 +2a^2 m+m^2 )/4)−((a^2 (a^2 +m))/2)} =((a^2 m+m^2 )/2)+{(((−a^4 )/4))−(((a^4 +2a^2 m+m^2 −2a^4 −2a^2 m)/4))} =((a^2 m+m^2 )/2)+{((−a^4 −a^4 −2a^2 m−m^2 +2a^4 +2a^2 m)/4)} =((a^2 m+m^2 )/2)−(m^2 /4) =((2a^2 m+2m^2 −m^2 )/4) =((2a^2 m+m^2 )/4) ((2a^2 m+m^2 )/4)=(a^4 /8) 4a^2 m+2m^2 −a^4 =0 2m^2 +4a^2 m−a^4 =0 m=((−4a^2 ±(√(16a^4 +8a^4 )) )/4) =((−4a^2 ±2(√6) a^2 )/4)=((−2a^2 ±(√6) a^2 )/2) as per figure m is negdtive m=((−a^2 (2+(√6) ))/2) pls check$
	$s o l v i n g m x = x (x^{2} - a^{2})$ $x {m - (x^{2} - a^{2}} = 0$ $x = 0$ $x^{2} - a^{2} = m$ $x = \pm \sqrt{a^{2} + m}$ $y = m x i n t e r s e c t t h e c u r v e a t {- \sqrt{a^{2} + m}, 0, \sqrt{a^{2} + m}}$ $t h e c u r v e y = x (x^{2} - a^{2}) i n t e r s e c t x a x i s a t {- a, 0, a}$ $n o w a r e a o f d o t s h a d e d + l i n e s h a d e d =$ $\int_{0}^{a} x (x^{2} - a^{2}) d x$ $= \int_{0}^{a} x^{3} - x^{} a^{2} d x$ $=∣ \frac{x^{4}}{4} - \frac{x^{2}}{2} \times a^{2} ∣_{0}^{a}$ $= \frac{a^{4}}{4} - \frac{a^{4}}{2}$ $t a k i n g t h e m o d o f v a l u e o f a r e a = \frac{a^{4}}{4}$ $s o d o t s h a d e d = \frac{a^{4}}{8}$ $l i n e s h a d e d = \frac{a^{4}}{8}$ $a r e a l i n e s h a d e d$ $\int_{0}^{\sqrt{a^{2} + m}} m x d x + \int_{\sqrt{a^{2} + m}}^{a} x (x^{2} - a^{2}) d x$ $=∣ \frac{{m x}^{2}}{2} ∣_{0}^{\sqrt{a^{2} + m}} + ∣ \frac{x^{4}}{4} - \frac{x^{2} a^{2}}{2} ∣_{\sqrt{a^{2} + m}}^{a}$ $= \frac{m (a^{2} + m)}{2} + {(\frac{a^{4}}{4} - \frac{a^{4}}{2}) - (\frac{a^{4} + 2 a^{2} m + m^{2}}{4} - \frac{a^{2} (a^{2} + m)}{2}}$ $= \frac{a^{2} m + m^{2}}{2} + {(\frac{- a^{4}}{4}) - (\frac{a^{4} + 2 a^{2} m + m^{2} - 2 a^{4} - 2 a^{2} m}{4})}$ $= \frac{a^{2} m + m^{2}}{2} + {\frac{- a^{4} - a^{4} - 2 a^{2} m - m^{2} + 2 a^{4} + 2 a^{2} m}{4}}$ $= \frac{a^{2} m + m^{2}}{2} - \frac{m^{2}}{4}$ $= \frac{2 a^{2} m + 2 m^{2} - m^{2}}{4}$ $= \frac{2 a^{2} m + m^{2}}{4}$ $\frac{2 a^{2} m + m^{2}}{4} = \frac{a^{4}}{8}$ $4 a^{2} m + 2 m^{2} - a^{4} = 0$ $2 m^{2} + 4 a^{2} m - a^{4} = 0$ $m = \frac{- 4 a^{2} \pm \sqrt{16 a^{4} + 8 a^{4}}}{4}$ $= \frac{- 4 a^{2} \pm 2 \sqrt{6} a^{2}}{4} = \frac{- 2 a^{2} \pm \sqrt{6} a^{2}}{2}$ $a s p e r f i g u r e m i s n e g d t i v e$ $m = \frac{- a^{2} (2 + \sqrt{6})}{2}$ $p l s c h e c k$
	Commented by ajfour last updated on 10/Sep/18

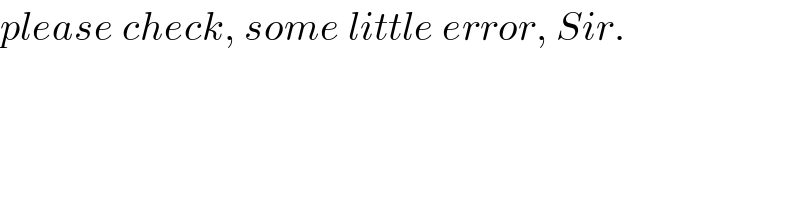
	$p l e a s e c h e c k, s o m e l i t t l e e r r o r, S i r .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

	$i h a v e d o n e$ $\int_{0}^{\sqrt{a^{2} + m}} m x + \int_{\sqrt{a^{2} + m}}^{a} x (x^{2} - a^{2}) d x t o f i n d t h e l i n e s h a d e d$ $a r e a$ $s u m o f t h e v a l u e o f t h i s t w o i n t r e g a l = \frac{a^{4}}{8}$ $b u t y o u h a v e d o n e$ $\int_{0}^{\sqrt{a^{2} + m}} m x - x (x^{2} - a^{2}) d x = \frac{a^{4}}{8}$ $p l s s a y w h i c h a r e a b e l o n g s t o t h i s i n t r e g a l$
	Commented by ajfour last updated on 10/Sep/18

	$t h e d o t s h a d e d a r e a i s e q u a l t o$ $w h a t i h a v e i n t e g r a t e d .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

	$i d o n o t a g r e e . . . \int_{0}^{\sqrt{a^{2} + m}} m x d x i s t h e a r e a o f t r i a n g l e$ $f o r m e d b y y = m x a n d x a x i s a n d s t l i n e x = \sqrt{a^{2} + m}$ $\int_{0}^{\sqrt{a^{2} + m}} x (x^{2} - a^{2}) d x$ $i s t h e a r e a f o r m e d b y x a x i s a n d c u r v e x (x^{2} - a^{2}) a n d s t$ $l i n e x = \sqrt{a^{2} + m} [$
	Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

	$p l s f i n d l i n e s h a d e d a r e a . . .$
	Commented by ajfour last updated on 10/Sep/18

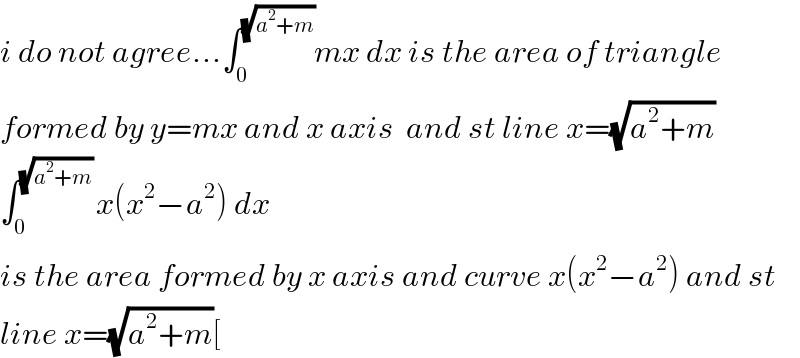
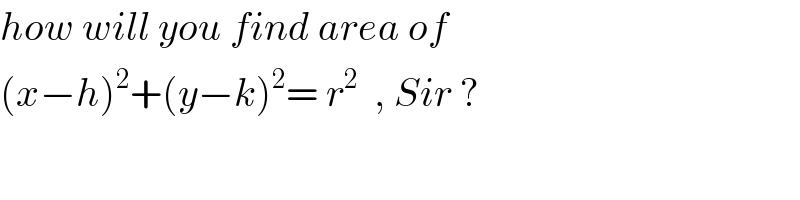
	$h o w w i l l y o u f i n d a r e a o f$ ${(x - h)}^{2} + {(y - k)}^{2} = r^{2}, S i r ?$
	Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

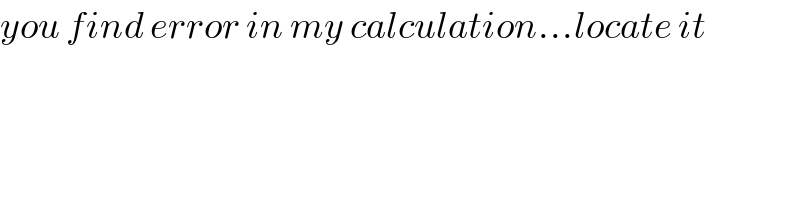
	$y o u f i n d e r r o r i n m y c a l c u l a t i o n . . . l o c a t e i t$
	Commented by ajfour last updated on 10/Sep/18

	$\int_{0}^{\sqrt{a^{2} + m}} m x d x + \int_{\sqrt{a^{2} + m}}^{a} x (x^{2} - a^{2}) d x = - \frac{a^{4}}{8}$ $(a r e a i s b e l o w x - a x i s s o - v e)$ $t h e n y o u s h a l l g e t$ $4 a^{2} m + 2 m^{2} + a^{4} = 0$ $\Rightarrow 2 m^{2} + 4 a^{2} m + a^{4} = 0$ $m = \frac{- 4 a^{2} \pm \sqrt{16 a^{4} - 8 a^{4}}}{4}$ $o r m = (- 1 + \frac{1}{\sqrt{2}}) a^{2}$ $(n o t a c c e p t i n g t h e o t h e r r o o t) .$
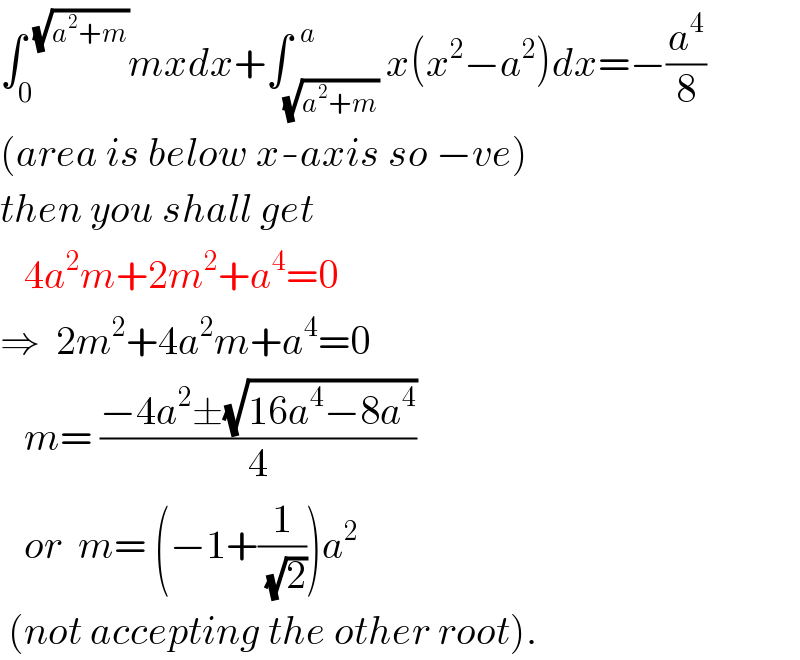
	Commented by tanmay.chaudhury50@gmail.com last updated on 11/Sep/18

	$o k t h a n k y o u . . .$
	Answered by MJS last updated on 10/Sep/18

	$p : y = x^{3} - a^{2} x$ $l : y = m x$ $p \cap l$ $x^{3} - (m + a^{2}) x = 0 \Rightarrow x = \sqrt{m + a^{2}}$ $dotted area : D = \underset{0}{\int^{\sqrt{m + a^{2}}}} (x^{3} - a^{2} x) d x - m \underset{0}{\int^{\sqrt{m + a^{2}}}} x d x$ $shaded area : S = m \underset{0}{\int^{\sqrt{m + a^{2}}}} x d x + \underset{\sqrt{m + a^{2}}}{\int^{a}} (x^{3} - a^{2} x) d x$ $D = \frac{1}{4} (m^{2} - a^{4}) - \frac{1}{2} m (m + a^{2}) = - \frac{1}{4} {(m + a^{2})}^{2}$ $S = \frac{1}{2} m (m + a^{2}) - \frac{1}{4} m^{2} = \frac{1}{4} m (m + 2 a^{2})$ $S - D = 0$ $m^{2} + 2 a^{2} m + \frac{a^{4}}{2} = 0$ $m = (- 1 + \frac{\sqrt{2}}{2}) a^{2} [the 2^{nd} solution {doesn}^{'} t$ $give a real value for \sqrt{m + a^{2}}]$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum