
Question and Answers Forum
Question Number 43539 by abdo.msup.com last updated on 11/Sep/18
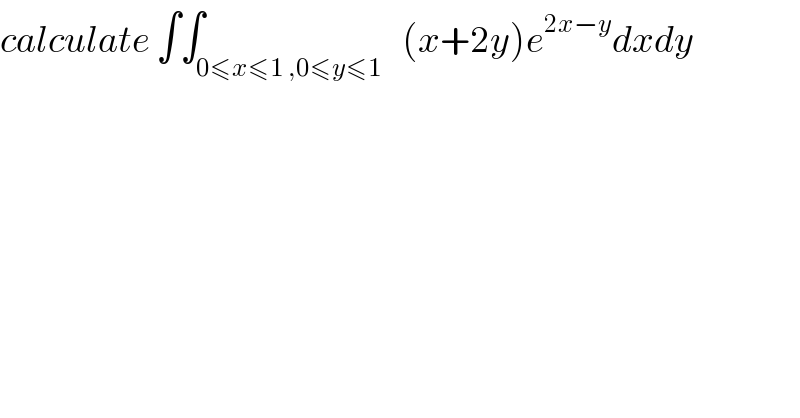
Commented by maxmathsup by imad last updated on 16/Sep/18
![let consider the diffeomorphisme (u,v) →ϕ(u,v)=(ϕ_1 (u,v),ϕ_2 (u,v))= (x,y) /u=x+2y and v=2x−y ⇒ { ((x+2y=u)),((2x−y=v ⇒ { ((2x+4y=2u)),((2x−y=v)) :})) :} ⇒ { ((5y=2u−v)),((x=u−2(((2u−v)/5)) ⇒ { ((y=(2/5)u−(1/5)v)),((x=(1/5)u +(2/5)v)) :})) :} ⇒ϕ(u,v)=(ϕ_1 ,ϕ_2 )=(x,y)=((1/5)u+(2/5)v,(2/5)u−(1/5)v)⇒ M_j (ϕ) = ((((∂ϕ_1 /∂u) (∂ϕ_1 /∂v))),(((∂ϕ_2 /∂u) (∂ϕ_2 /∂v))) ) = ((( (1/5) (2/5))),(((2/5) −(1/5))) ) and detM_j =−(1/(25)) −(4/(25)) =−(1/(25)) we have 0≤x≤1 and 0≤2y≤2 ⇒0≤x+2y≤3 ⇒0≤u≤3 0≤2x≤2 and −1≤−y≤0 ⇒−1≤2x−y≤ 2 ⇒−1≤v≤2 ⇒ ∫∫f(x,y)dxdy = ∫∫_w foϕ(u,v) ∣detM_j (ϕ)∣ du dv =∫∫_(0≤u≤3 and −1≤v≤2) u e^v (1/(25)) du dv =(1/(25)) ∫_0 ^3 udu .∫_(−1) ^2 e^v dv =(1/(25))[ (u^2 /2)]_0 ^3 .[ e^v ]_(−1) ^2 =(1/(50))(9)( e^2 −e^(−1) ) =(9/(50)){ e^2 −(1/e)} .](Q43849.png)
| ||
Question and Answers Forum | ||
Question Number 43539 by abdo.msup.com last updated on 11/Sep/18 | ||
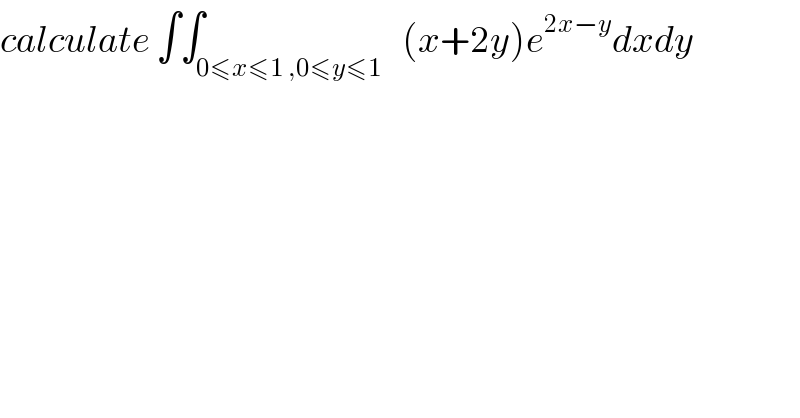 | ||
Commented by maxmathsup by imad last updated on 16/Sep/18 | ||
![let consider the diffeomorphisme (u,v) →ϕ(u,v)=(ϕ_1 (u,v),ϕ_2 (u,v))= (x,y) /u=x+2y and v=2x−y ⇒ { ((x+2y=u)),((2x−y=v ⇒ { ((2x+4y=2u)),((2x−y=v)) :})) :} ⇒ { ((5y=2u−v)),((x=u−2(((2u−v)/5)) ⇒ { ((y=(2/5)u−(1/5)v)),((x=(1/5)u +(2/5)v)) :})) :} ⇒ϕ(u,v)=(ϕ_1 ,ϕ_2 )=(x,y)=((1/5)u+(2/5)v,(2/5)u−(1/5)v)⇒ M_j (ϕ) = ((((∂ϕ_1 /∂u) (∂ϕ_1 /∂v))),(((∂ϕ_2 /∂u) (∂ϕ_2 /∂v))) ) = ((( (1/5) (2/5))),(((2/5) −(1/5))) ) and detM_j =−(1/(25)) −(4/(25)) =−(1/(25)) we have 0≤x≤1 and 0≤2y≤2 ⇒0≤x+2y≤3 ⇒0≤u≤3 0≤2x≤2 and −1≤−y≤0 ⇒−1≤2x−y≤ 2 ⇒−1≤v≤2 ⇒ ∫∫f(x,y)dxdy = ∫∫_w foϕ(u,v) ∣detM_j (ϕ)∣ du dv =∫∫_(0≤u≤3 and −1≤v≤2) u e^v (1/(25)) du dv =(1/(25)) ∫_0 ^3 udu .∫_(−1) ^2 e^v dv =(1/(25))[ (u^2 /2)]_0 ^3 .[ e^v ]_(−1) ^2 =(1/(50))(9)( e^2 −e^(−1) ) =(9/(50)){ e^2 −(1/e)} .](Q43849.png) | ||