
Question and Answers Forum
Question Number 43545 by peter frank last updated on 11/Sep/18
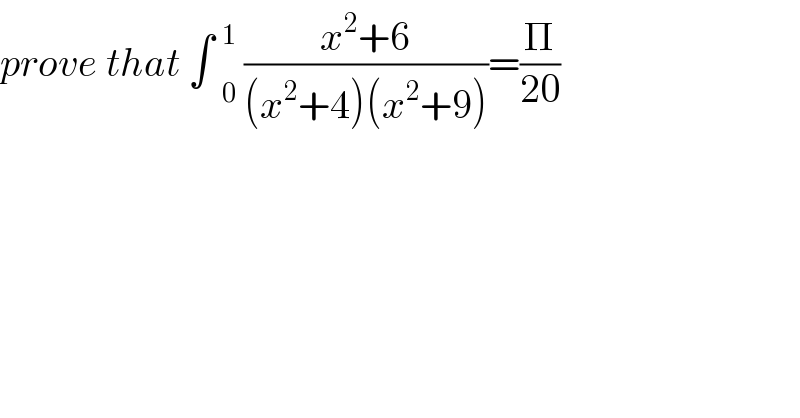
Answered by behi83417@gmail.com last updated on 12/Sep/18
![I=(1/2)∫((2x^2 +12)/((x^2 +4)(x^2 +9)))dx= =(1/2)[∫((1/(x^2 +9))+(1/(x^2 +4))−(1/5)((1/(x^2 +4))−(1/(x^2 +9)))]dx= =(3/5)∫ (dx/(x^2 +9))+(2/5)∫ (dx/(x^2 +4))= =(3/5).(1/3)tg^(−1) ((x/3))+(2/5).(1/2)tg^(−1) ((x/2))+c= =(1/5)tg^(−1) (((x/3)+(x/2))/(1−(x^2 /6)))=(1/5)tg^(−1) ((5x)/(6−x^2 ))+c. I=F(1)−F(0)=(1/5)[tg^(−1) (5/5)−0]= =(1/5).(π/4)=(π/(20)). ■](Q43553.png)
| ||
Question and Answers Forum | ||
Question Number 43545 by peter frank last updated on 11/Sep/18 | ||
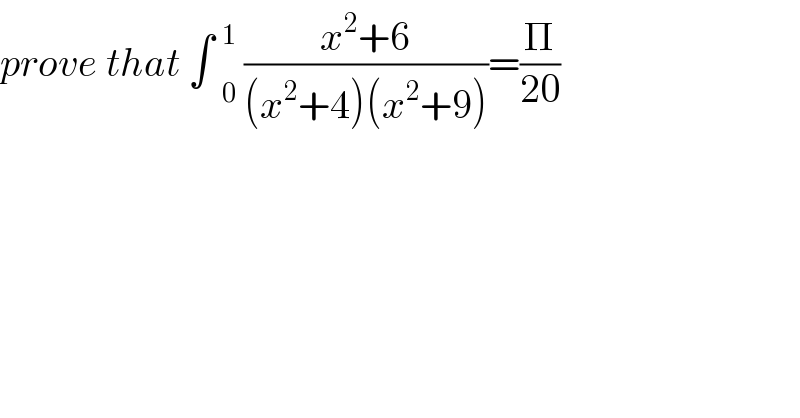 | ||
Answered by behi83417@gmail.com last updated on 12/Sep/18 | ||
![I=(1/2)∫((2x^2 +12)/((x^2 +4)(x^2 +9)))dx= =(1/2)[∫((1/(x^2 +9))+(1/(x^2 +4))−(1/5)((1/(x^2 +4))−(1/(x^2 +9)))]dx= =(3/5)∫ (dx/(x^2 +9))+(2/5)∫ (dx/(x^2 +4))= =(3/5).(1/3)tg^(−1) ((x/3))+(2/5).(1/2)tg^(−1) ((x/2))+c= =(1/5)tg^(−1) (((x/3)+(x/2))/(1−(x^2 /6)))=(1/5)tg^(−1) ((5x)/(6−x^2 ))+c. I=F(1)−F(0)=(1/5)[tg^(−1) (5/5)−0]= =(1/5).(π/4)=(π/(20)). ■](Q43553.png) | ||
| ||