Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 4363 by Rasheed Soomro last updated on 13/Jan/16

If lim_(x→a) ((f(x))/(g(x))) exists and lim_(x→a) g(x)=0, then show that lim_(x→a) f(x)=0.

$${If}\:\:\underset{{x}\rightarrow{a}} {{lim}}\:\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\:{exists}\:{and}\:\underset{{x}\rightarrow{a}} {{lim}}\:{g}\left({x}\right)=\mathrm{0}, \\ $$$${then}\:{show}\:{that} \\ $$$$\underset{{x}\rightarrow{a}} {{lim}}\:{f}\left({x}\right)=\mathrm{0}. \\ $$

Answered by Yozzii last updated on 13/Jan/16

Let l=lim_(x→a) ((f(x))/(g(x))) and h(x)=((f(x))/(g(x))) (g(x)≠0). l exists if, for every ε>0 there exists a δ>0 such that ∣h(x)−l∣<ε whenever 0<∣x−a∣<δ. ∴∣((f(x))/(g(x)))−lim_(x→a) ((f(x))/(g(x)))∣<ε ∣((f(x))/(g(x)))−((lim_(x→a) f(x))/(lim_(x→a) g(x)))∣<ε ∣((f(x)×lim_(x→a) g(x)−g(x)lim_(x→a) f(x))/(g(x)lim_(x→a) g(x)))∣<ε ∴∣f(x)lim_(x→a) g(x)−g(x)lim_(x→a) f(x)∣<ε∣g(x)lim_(x→a) g(x)∣ Since lim_(x→a) g(x)=0 we have ∣0−g(x)lim_(x→a) f(x)∣<0 Hence ∣−g(x)lim_(x→a) f(x)∣<0 which is false. (If indeed lim_(x→a) f(x)=0, there exists some error in my use of the ε−δ definition of the limit.)

$${Let}\:{l}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\:{and}\:{h}\left({x}\right)=\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\:\left({g}\left({x}\right)\neq\mathrm{0}\right).\:{l}\:{exists}\:{if},\:{for}\:{every} \\ $$$$\epsilon>\mathrm{0}\:{there}\:{exists}\:{a}\:\delta>\mathrm{0}\:{such}\:{that} \\ $$$$\mid{h}\left({x}\right)−{l}\mid<\epsilon\:{whenever}\:\mathrm{0}<\mid{x}−{a}\mid<\delta. \\ $$$$\therefore\mid\frac{{f}\left({x}\right)}{{g}\left({x}\right)}−\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\mid<\epsilon \\ $$$$\mid\frac{{f}\left({x}\right)}{{g}\left({x}\right)}−\frac{\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)}{\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)}\mid<\epsilon \\ $$$$\mid\frac{{f}\left({x}\right)×\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)−{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)}{{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)}\mid<\epsilon \\ $$$$\therefore\mid{f}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)−{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)\mid<\epsilon\mid{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)\mid \\ $$$${Since}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)=\mathrm{0}\:{we}\:{have} \\ $$$$\mid\mathrm{0}−{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)\mid<\mathrm{0} \\ $$$${Hence}\:\mid−{g}\left({x}\right)\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)\mid<\mathrm{0}\:{which}\:{is}\:{false}. \\ $$$$ \\ $$$$\left({If}\:{indeed}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{0},\:{there}\:{exists}\right. \\ $$$${some}\:{error}\:{in}\:{my}\:{use}\:{of}\:{the}\:\epsilon−\delta\: \\ $$$$\left.{definition}\:{of}\:{the}\:{limit}.\right) \\ $$

Commented by prakash jain last updated on 13/Jan/16

lim_(x→3) ((x^2 −9)/(x−3))

$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{9}}{{x}−\mathrm{3}} \\ $$

Commented by Yozzii last updated on 13/Jan/16

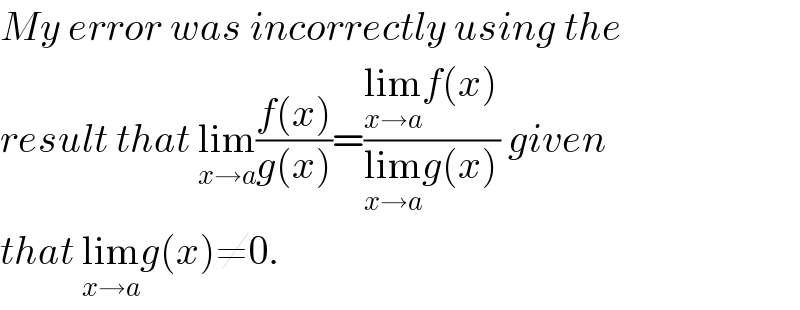
My error was incorrectly using the result that lim_(x→a) ((f(x))/(g(x)))=((lim_(x→a) f(x))/(lim_(x→a) g(x))) given that lim_(x→a) g(x)≠0.

$${My}\:{error}\:{was}\:{incorrectly}\:{using}\:{the}\: \\ $$$${result}\:{that}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\frac{\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)}{\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)}\:{given} \\ $$$${that}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}{g}\left({x}\right)\neq\mathrm{0}. \\ $$

Answered by RasheedSindhi last updated on 14/Jan/16

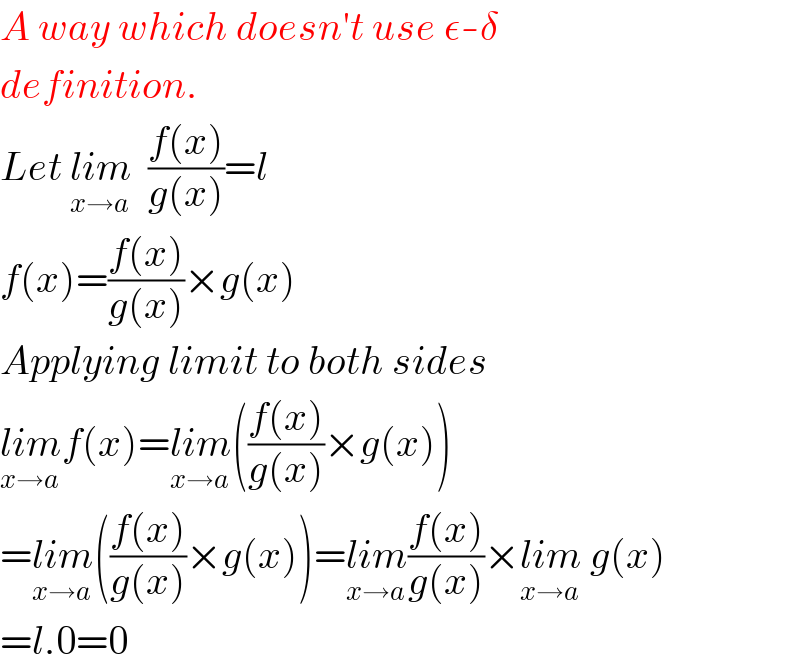
A way which doesn′t use ε-δ definition. Let lim_(x→a) ((f(x))/(g(x)))=l f(x)=((f(x))/(g(x)))×g(x) Applying limit to both sides lim_(x→a) f(x)=lim_(x→a) (((f(x))/(g(x)))×g(x)) =lim_(x→a) (((f(x))/(g(x)))×g(x))=lim_(x→a) ((f(x))/(g(x)))×lim_(x→a) g(x) =l.0=0

$${A}\:{way}\:{which}\:{doesn}'{t}\:{use}\:\epsilon-\delta \\ $$$${definition}. \\ $$$${Let}\:\underset{{x}\rightarrow{a}} {{lim}}\:\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}={l} \\ $$$${f}\left({x}\right)=\frac{{f}\left({x}\right)}{{g}\left({x}\right)}×{g}\left({x}\right) \\ $$$${Applying}\:{limit}\:{to}\:{both}\:{sides} \\ $$$$\underset{{x}\rightarrow{a}} {{lim}f}\left({x}\right)=\underset{{x}\rightarrow{a}} {{lim}}\left(\frac{{f}\left({x}\right)}{{g}\left({x}\right)}×{g}\left({x}\right)\right) \\ $$$$=\underset{{x}\rightarrow{a}} {{lim}}\left(\frac{{f}\left({x}\right)}{{g}\left({x}\right)}×{g}\left({x}\right)\right)=\underset{{x}\rightarrow{a}} {{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}×\underset{{x}\rightarrow{a}} {{lim}}\:{g}\left({x}\right) \\ $$$$={l}.\mathrm{0}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com