Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 43657 by Tinkutara last updated on 13/Sep/18

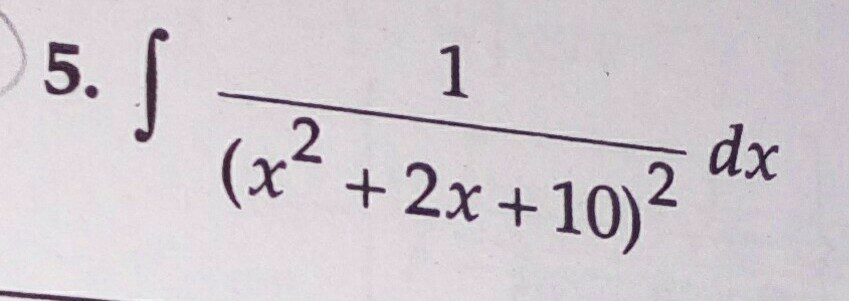
Commented by maxmathsup by imad last updated on 24/Sep/18
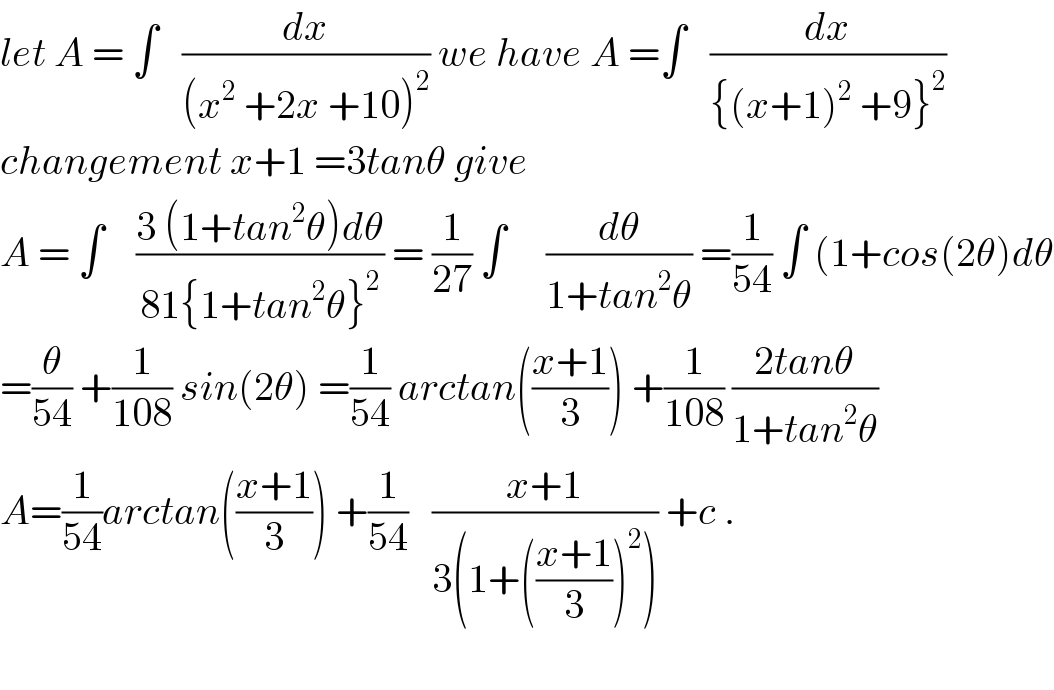
$let A = ∫ (dx/((x^2 +2x +10)^2 )) we have A =∫ (dx/({(x+1)^2 +9}^2 )) changement x+1 =3tanθ give A = ∫ ((3 (1+tan^2 θ)dθ)/(81{1+tan^2 θ}^2 )) = (1/(27)) ∫ (dθ/(1+tan^2 θ)) =(1/(54)) ∫ (1+cos(2θ)dθ =(θ/(54)) +(1/(108)) sin(2θ) =(1/(54)) arctan(((x+1)/3)) +(1/(108)) ((2tanθ)/(1+tan^2 θ)) A=(1/(54))arctan(((x+1)/3)) +(1/(54)) ((x+1)/(3(1+(((x+1)/3))^2 ))) +c .$
$l e t A = \int \frac{d x}{{(x^{2} + 2 x + 10)}^{2}} w e h a v e A = \int \frac{d x}{{{(x + 1)}^{2} + 9}^{2}}$ $c h a n g e m e n t x + 1 = 3 t a n θ g i v e$ $A = \int \frac{3 (1 + {t a n}^{2} θ) d θ}{81 {1 + {t a n}^{2} θ}^{2}} = \frac{1}{27} \int \frac{d θ}{1 + {t a n}^{2} θ} = \frac{1}{54} \int (1 + c o s (2 θ) d θ$ $= \frac{θ}{54} + \frac{1}{108} s i n (2 θ) = \frac{1}{54} a r c t a n (\frac{x + 1}{3}) + \frac{1}{108} \frac{2 t a n θ}{1 + {t a n}^{2} θ}$ $A = \frac{1}{54} a r c t a n (\frac{x + 1}{3}) + \frac{1}{54} \frac{x + 1}{3 (1 + {(\frac{x + 1}{3})}^{2})} + c .$
	Answered by ajfour last updated on 13/Sep/18

	$\int \frac{d x}{{[{(x + 1)}^{2} + 3^{2}]}^{2}}$ $l e t x + 1 = 3 \tan θ$ $\Rightarrow \int \frac{3 \sec^{2} θ d θ}{81 \sec^{4} θ} = \frac{1}{54} \int 2 \cos^{2} θ d θ + c$ $. . . .$ $= \frac{1}{54} [\tan^{- 1} (\frac{x + 1}{3}) + \frac{3 (x + 1)}{(x^{2} + 2 x + 10)}] + c .$
	Commented by Tinkutara last updated on 14/Sep/18
	Thank you very much Sir! But in answer there is no multiplication with 3 in numerator of 2nd term.
	Commented by Tinkutara last updated on 14/Sep/18

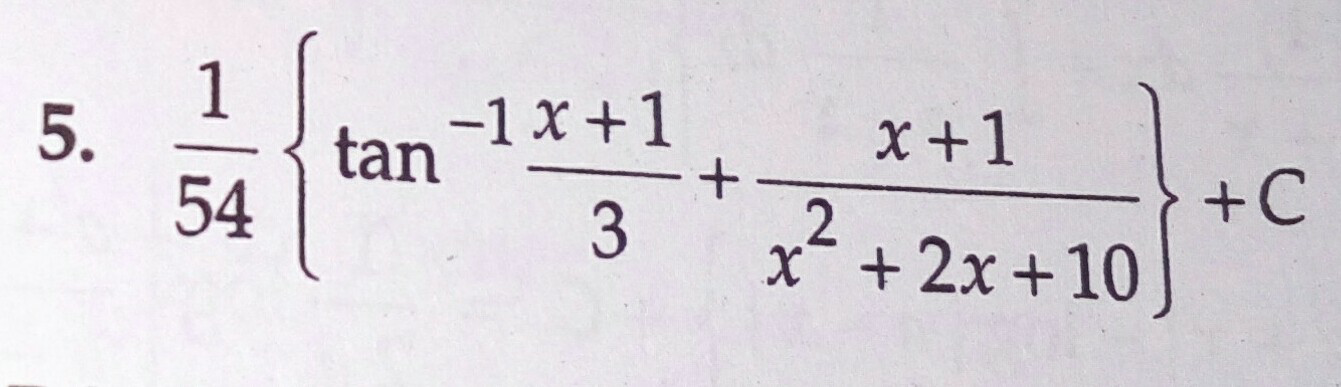
	Commented by MJS last updated on 14/Sep/18

	$\frac{d}{d x} [\frac{1}{54} (\arctan \frac{x + 1}{3} + \frac{x + 1}{x^{2} + 2 x + 10}] =$ $= \frac{1}{54} (\frac{1}{3 (\frac{{(x + 1)}^{2}}{9} + 1)} + \frac{x^{2} + 2 x + 10 - (x + 1) (2 x + 2)}{{(x^{2} + 2 x + 10)}^{2}})$ $= \frac{1}{54} (\frac{3}{x^{2} + 2 x + 10} + \frac{- x^{2} - 2 x + 8}{{(x^{2} + 2 x + 10)}^{2}}) =$ $= \frac{1}{27} \times \frac{x^{2} + 2 x + 19}{{(x^{2} + 2 x + 10)}^{2}}$ $so the book is wrong$
	Commented by Tinkutara last updated on 14/Sep/18
	Thank you Sir!
	Answered by tanmay.chaudhury50@gmail.com last updated on 14/Sep/18
	$∫(dx/({(x+1)^2 +3^2 }^2 )) x+1=3tanα dx=3sec^2 αdα ∫((3sec^2 αdα)/({3^2 (1+tan^2 α)}^2 )) (1/(27))∫((sec^2 αdα)/(sec^4 α)) (1/(27))∫((1+cos2α)/2)dα (1/(54)){α+((sin2α)/2)}+c (1/(54)){tan^(−1) (((x+1)/3))+(1/2)×((2tanα)/(1+tan^2 α))} (1/(54)){tan^(−1) (((x+1)/3))+(((x+1)/3)/(1+(((x+1)/3))^2 ))}+c (1/(54)){tan^(−1) (((x+1)/3))+((3(x+1))/(x^2 +2x+10))}+c$
	$\int \frac{d x}{{{(x + 1)}^{2} + 3^{2}}^{2}}$ $x + 1 = 3 t a n α$ $d x = 3 {s e c}^{2} α d α$ $\int \frac{3 {s e c}^{2} α d α}{{3^{2} (1 + {t a n}^{2} α)}^{2}}$ $\frac{1}{27} \int \frac{{s e c}^{2} α d α}{{s e c}^{4} α}$ $\frac{1}{27} \int \frac{1 + c o s 2 α}{2} d α$ $\frac{1}{54} {α + \frac{s i n 2 α}{2}} + c$ $\frac{1}{54} {{t a n}^{- 1} (\frac{x + 1}{3}) + \frac{1}{2} \times \frac{2 t a n α}{1 + {t a n}^{2} α}}$ $\frac{1}{54} {{t a n}^{- 1} (\frac{x + 1}{3}) + \frac{\frac{x + 1}{3}}{1 + {(\frac{x + 1}{3})}^{2}}} + c$ $\frac{1}{54} {{t a n}^{- 1} (\frac{x + 1}{3}) + \frac{3 (x + 1)}{x^{2} + 2 x + 10}} + c$
	Commented by Tinkutara last updated on 14/Sep/18
	Thanks very much Sir! But please check the answer in book.
	Answered by MJS last updated on 14/Sep/18

	$\int \frac{d x}{{(x^{2} + 2 x + 10)}^{2}} = \int \frac{d x}{{({(x + 1)}^{2} + 9)}^{2}} =$ $[t = x + 1 \to d x = d t]$ $= \int \frac{d t}{{(t^{2} + 9)}^{2}} =$ $[reduction formula$ $\int \frac{d t}{{({a t}^{2} + b)}^{n}} = \frac{t}{2 b (n - 1) {({a t}^{2} + b)}^{n - 1}} + \frac{2 n - 3}{2 b (n - 1)} \int \frac{d t}{{({a t}^{2} + b)}^{n - 1}}]$ $= \frac{t}{18 (t^{2} + 9)} + \frac{1}{18} \int \frac{d t}{t^{2} + 9} =$ $\int \frac{d t}{t^{2} + 9} =$ $[u = \frac{t}{3} \to d t = 3 d u]$ $= \frac{1}{3} \int \frac{d u}{u^{2} + 1} = \frac{1}{3} \arctan u = \frac{1}{3} \arctan \frac{t}{3}$ $= \frac{t}{18 (t^{2} + 9)} + \frac{1}{54} \arctan \frac{t}{3} =$ $= \frac{x + 1}{18 (x^{2} + 2 x + 10)} + \frac{1}{54} \arctan \frac{x + 1}{3} + C$
	Commented by Tinkutara last updated on 14/Sep/18
	Thanks very much.
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum