Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 43699 by Meritguide1234 last updated on 14/Sep/18

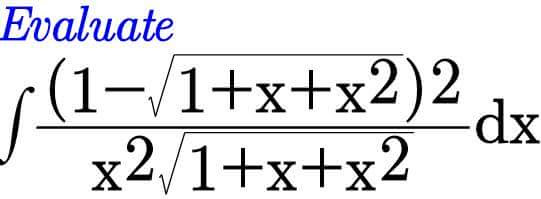
Commented by Meritguide1234 last updated on 14/Sep/18

$$completeit$$

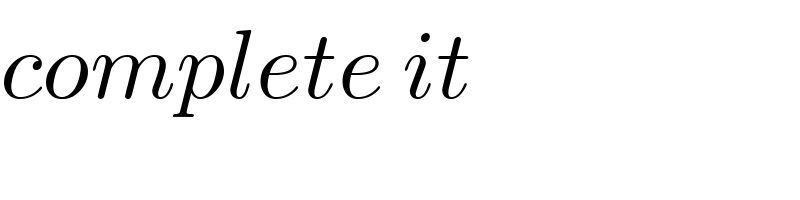
Commented by maxmathsup by imad last updated on 14/Sep/18

$$letI=\int \frac{{(1-\sqrt{1+x+x^2})}^2}{x^2\sqrt{1+x+x^2}}dxwehaveI=\int \frac{1-2\sqrt{1+x+x^2}+1+x+x^2}{x^2\sqrt{1+x+x^2}}dx$$$$=\int \frac{dx}{x^2\sqrt{1+x+x^2}}dx-2\int \frac{dx}{x^2}+\int \frac{\sqrt{1+x+x^2}}{x^2}dxbut$$$$-2\int \frac{dx}{x^2}=\frac{2}{x}+cand\int \frac{dx}{x^2\sqrt{1+x+x^2}}=\int \frac{dx}{x^2\sqrt{{(x+\frac{1}{2})}^2+\frac{3}{4}}}$$$${=}_{x+\frac{1}{2}=\frac{\sqrt{3}}{2}sh\left(t\right)}\int \frac{1}{{(\frac{\sqrt{3}}{2}sh\left(t\right)-\frac{1}{2})}^2\frac{\sqrt{3}}{2}ch\left(t\right)}\frac{\sqrt{3}}{2}ch\left(t\right)dt$$$$=\int \frac{4dt}{{(\sqrt{3}sh\left(t\right)-1)}^2}=\int \frac{4dt}{3{sh}^2\left(t\right)-2\sqrt{3}sh\left(t\right)+1}$$$$=\int \frac{4dt}{3\frac{1+ch\left(2t\right)}{2}-2\sqrt{3}sh\left(t\right)+1}=8\int \frac{dt}{3+3ch\left(2t\right)-4\sqrt{3}sh\left(t\right)+2}$$$$=8\int \frac{dt}{3+3\frac{e^{2t}+e^{-2t}}{2}-4\sqrt{3}\frac{e^t-e^{-t}}{2}+2}=16\int \frac{dt}{6+3e^{2t}+3e^{-2t}-4\sqrt{3}{e}^t+4\sqrt{3}{e}^{-t}+4}$$$${=}_{e^t=u}16\int \frac{du}{u\{10+3u^2+3u^{-2}-4\sqrt{3}u+4\sqrt{3}{u}^{-1}\}}$$$$=16\int \frac{du}{10u+3u^3+3u^{-1}-4\sqrt{3}{u}^2+4\sqrt{3}}$$$$=16\int \frac{udu}{10u^2+3u^4+3-4\sqrt{3}{u}^3+4\sqrt{3}u}letdecompose$$$$F\left(u\right)=\frac{u}{3u^4-4\sqrt{3}{u}^3+10u^2+4\sqrt{3}u+3}...becontinued...$$

Commented by MJS last updated on 14/Sep/18

$${\mathrm{there}}^{\prime }\mathrm{s}\mathrm{a}\mathrm{magic}\mathrm{word}\mathrm{and}\mathrm{I}\mathrm{seem}\mathrm{to}\mathrm{remember}$$$$\mathrm{it}\mathrm{starts}\mathrm{with}‘‘{\mathrm{p}}^{″}.$$

Commented by Meritguide1234 last updated on 15/Sep/18

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Sep/18

$$\int \frac{1-2\sqrt{1+x+x^2}+1+x+x^2}{x^2\sqrt{1+x+x^2}}dx$$$$\int \frac{dx}{x^2\sqrt{1+x+x^2}}-2\int \frac{dx}{x^2}+\int \frac{\sqrt{1+x+x^2}}{x^2}dx$$$$I=I_1-2I_2+I_3$$$$I_1=\int \frac{dx}{x^2\sqrt{1+x+x^2}}$$$$t=\frac{1}{x}dx$$$$dt=-\frac{dx}{x^2}$$$$\int \frac{-dt}{\sqrt{1+\frac{1}{t}+\frac{1}{t^2}}}$$$$\int \frac{-tdt}{\sqrt{t^2+t+1}}\frac{}{}$$$$\frac{-1}{2}\int \frac{2t+1-1}{\sqrt{t^2+t+1}}dt$$$$=\frac{1}{2}\int \frac{dt}{\sqrt{t^2+t+1}}-\frac{1}{2}\int \frac{d(t^2+t+1)}{\sqrt{t^2+t+1}}$$$$=\frac{1}{2}\int \frac{dt}{\sqrt{t^2+2.t.\frac{1}{2}+\frac{1}{4}+1-\frac{1}{4}}}-\frac{1}{2}\int \frac{d(t^2+t+1)}{\sqrt{t^2+t+1}}dt$$$$=\frac{1}{2}\int \frac{dt}{\sqrt{{(t+\frac{1}{2})}^2+{\left(\frac{\sqrt{3}}{2}\right)}^2}}-\frac{1}{2}\int \frac{d(t^2+t+1)}{\sqrt{t^2+t+1}}$$$$=\frac{1}{2}ln\{(t+\frac{1}{2})+\sqrt{t^2+t+1}\}-\frac{1}{2}\times \frac{\sqrt{t^2+t+1}}{\frac{1}{2}}$$$$=\frac{1}{2}ln\{(t+\frac{1}{2})+\sqrt{t^2+t+1}\}-\sqrt{t^2+t+1}$$$$=\frac{1}{2}ln\{(\frac{1}{x}+\frac{1}{2})+\sqrt{\frac{1}{x^2}+\frac{1}{x}+1}\}-\sqrt{\frac{1}{x^2}+\frac{1}{x}+1}$$$$I_2=\int \frac{dx}{x^2}=\frac{x^{-1}}{-1}=\frac{-1}{x}$$$$I_3=\int \frac{\sqrt{1+x+x^2}}{x^2}$$$$=\int \frac{1+x+x^2}{x^2\sqrt{1+x+x^2}}dx$$$$=\int \frac{dx}{x^2\sqrt{1+x+x^2}}+\int \frac{dx}{x\sqrt{1+x+x^2}}+\int \frac{dx}{\sqrt{1+x+x^2}}$$$$=sameas{I}_1+\int \frac{dx}{x\sqrt{1+x+x^2}}+\int \frac{dx}{\sqrt{{(x+\frac{1}{2})}^2+{\left(\frac{\sqrt{3}}{2}\right)}^2}}$$$$=sameas{I}_1+ln\{(x+\frac{1}{2})+\sqrt{x^2+x+1}\}+\int \frac{dx}{x\sqrt{1+x+x^2}}$$$$=\frac{1}{2}ln\{(\frac{1}{x}+\frac{1}{2})+\sqrt{\frac{1}{x^2}+\frac{1}{x}+1}\}-\sqrt{\frac{1}{x^2}+\frac{1}{x}+1}+$$$$ln\{(x+\frac{1}{2}+\sqrt{x^2+x+1}\}+\int \frac{dx}{x\sqrt{1+x+x^2}}$$$$\int \frac{dx}{x\sqrt{1+x+x^2}}$$$$x=\frac{1}{t}dx=\frac{-1}{t^2}dt$$$$\int \frac{-dt}{t^2\times \frac{1}{t}\times \sqrt{1+\frac{1}{t}+\frac{1}{t^2}}}$$$$\int \frac{-dt}{\sqrt{t^2+t+1}}$$$$=-ln\{t+\frac{1}{2})+\sqrt{t^2+t+1}\}$$$$=-ln[(\frac{1}{x}+\frac{1}{2})+\left\{\sqrt{\frac{1}{x^2}+\frac{1}{x}+1}\right\}]$$$$\mathit{N}OWPLSputthevalueof{I}_1-2I_2+I_3$$$$$$$$$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com