let ϕ(a,x) =∫_0 ^(π/2) (dt/(x+asin^2 t)) 2) find a exlicite form of ϕ(a,x) 3)determine ϕ(1,x)and ϕ(a,1) 4)find the vslue of ∫_0 ^(π/2) (dt/(2+3sin^2 t)) 5)find ∫_0 ^(π/2) (dt/((x+asin^2 t)^2 )) 6) find ∫_0 ^(π/2) ((sin^2 t)/((x+a sin^2 t)^2 ))dt .


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 43823 by abdo.msup.com last updated on 15/Sep/18

$l e t φ (a, x) = \int_{0}^{\frac{π}{2}} \frac{d t}{x + {a s i n}^{2} t}$ $2) f i n d a e x l i c i t e f o r m o f φ (a, x)$ $3) d e t e r m i n e φ (1, x) a n d φ (a, 1)$ $4) f i n d t h e v s l u e o f \int_{0}^{\frac{π}{2}} \frac{d t}{2 + 3 {s i n}^{2} t}$ $5) f i n d \int_{0}^{\frac{π}{2}} \frac{d t}{{(x + {a s i n}^{2} t)}^{2}}$ $6) f i n d \int_{0}^{\frac{π}{2}} \frac{{s i n}^{2} t}{{(x + a {s i n}^{2} t)}^{2}} d t .$
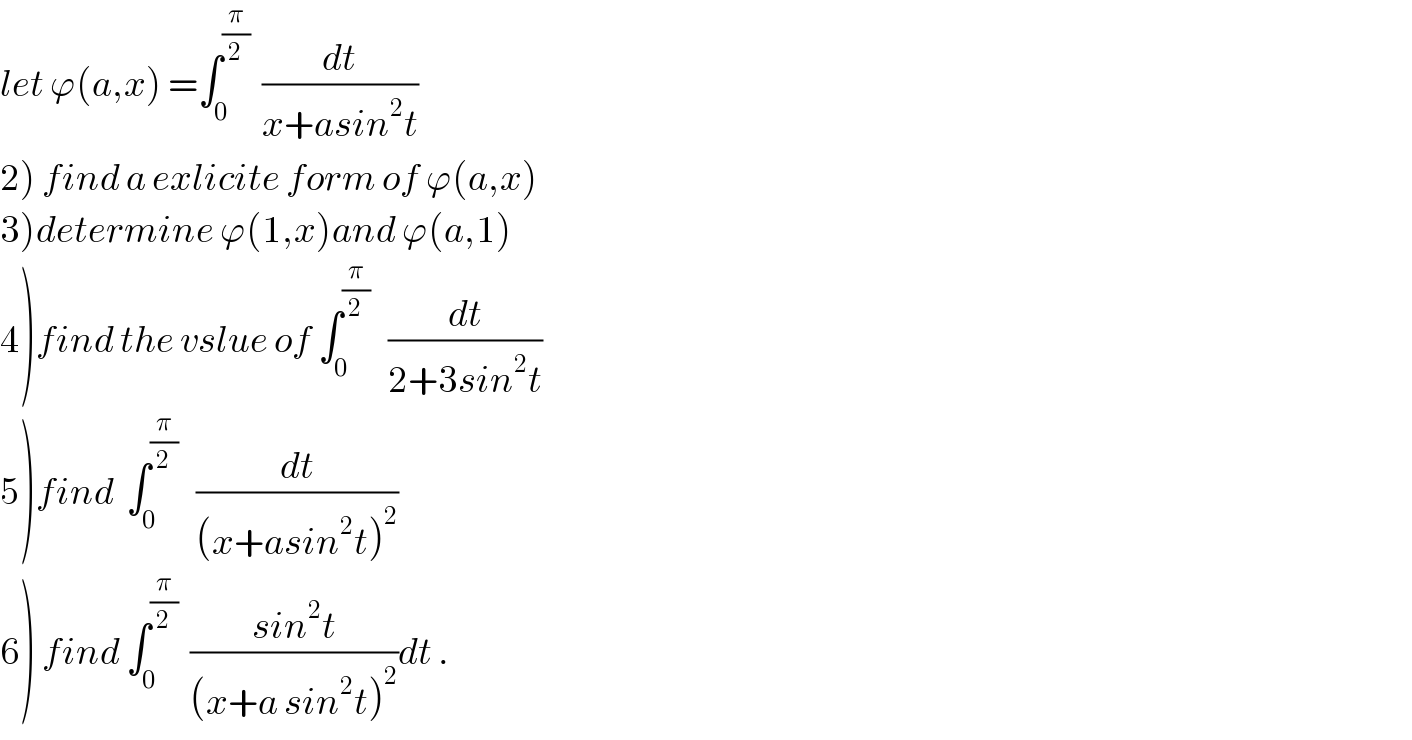
Commented by maxmathsup by imad last updated on 17/Sep/18
$1) we have ϕ(a,x) =∫_0 ^(π/2) (dt/(x+a ((1−cos(2t))/2))) = ∫_0 ^(π/2) ((2dt)/(2x +a −a cos(2t))) =_(2t =u) ∫_0 ^π (du/(2x +a−acosu)) =_(tan((u/2))=α) ∫_0 ^∞ (1/(2x+a−a((1−α^2 )/(1+α^2 )))) ((2dα)/(1+α^2 )) = ∫_0 ^∞ ((2 dα)/((2x+1)(1+α^2 )−a(1−α^2 ))) =∫_0 ^∞ ((2dα)/((2x+1) +(2x+1 +a)α^2 −a)) = ∫_0 ^∞ ((2dα)/((2x+1+a)α^2 + 2x+1−a)) =(2/((2x+1+a))) ∫_0 ^∞ (dα/(α^2 +((2x+1−a)/(2x+1+a)))) case 1 ((2x+1−a)/(2x+1+a))>0 changement α =(√((2x+1−a)/(2x+1+a)))z give ϕ(a,x) = (2/((2x+1+a))) ∫_0 ^∞ (1/(((2x+1−a)/(2x+1 +a))(1+z^2 ))) (√((2x+1−a)/(2x+1+a)))dz =(2/(2x+1+a)) ((2x+1+a)/(2x+1−a)) (√((2x+1−a)/(2x+1+a)))(π/2) =(π/(2x+1+a)) (√((2x+1+a)/(2x+1−a))) = (π/(√((2x+1+a)^2 −a^2 ))) case 2 ((2x+1−a)/(2x+1 +a))<0 ⇒ϕ(a,x) = (2/(2x+1+a)) ∫_0 ^∞ (dα/(α^2 −((a−(2x+1))/(a+2x+1)))) changement α =(√((a−(2x+1))/(a+2x+1)))z give ϕ(a,x) = (2/(2x+1+a)) ∫_0 ^∞ (1/(((a−(2x+1))/(a+2x+1))(z^2 −1))) (√((a−(2x+1))/(a+(2x+1)))) dz = (2/(2x+1+a)) ((a +2x+1)/(a−(2x+1))) (√((a−(2x+1))/(a+(2x+1))))∫_0 ^∞ (dz/(z^2 −1)) = (π/(√(a^2 −(2x+1)^2 ))) (1/2)∫_0 ^∞ {(1/(z−1)) −(1/(z+1))}dz =(π/(2(√(a^2 −(2x+1)^2 ))))[ln∣((z−1)/(z+1))∣]_0 ^(+∞) =0$
$1) w e h a v e φ (a, x) = \int_{0}^{\frac{π}{2}} \frac{d t}{x + a \frac{1 - c o s (2 t)}{2}} = \int_{0}^{\frac{π}{2}} \frac{2 d t}{2 x + a - a c o s (2 t)}$ $=_{2 t = u} \int_{0}^{π} \frac{d u}{2 x + a - a c o s u} =_{t a n (\frac{u}{2}) = α} \int_{0}^{\infty} \frac{1}{2 x + a - a \frac{1 - α^{2}}{1 + α^{2}}} \frac{2 d α}{1 + α^{2}}$ $= \int_{0}^{\infty} \frac{2 d α}{(2 x + 1) (1 + α^{2}) - a (1 - α^{2})} = \int_{0}^{\infty} \frac{2 d α}{(2 x + 1) + (2 x + 1 + a) α^{2} - a}$ $= \int_{0}^{\infty} \frac{2 d α}{(2 x + 1 + a) α^{2} + 2 x + 1 - a} = \frac{2}{(2 x + 1 + a)} \int_{0}^{\infty} \frac{d α}{α^{2} + \frac{2 x + 1 - a}{2 x + 1 + a}}$ $c a s e 1 \frac{2 x + 1 - a}{2 x + 1 + a} > 0 c h a n g e m e n t α = \sqrt{\frac{2 x + 1 - a}{2 x + 1 + a}} z g i v e$ $φ (a, x) = \frac{2}{(2 x + 1 + a)} \int_{0}^{\infty} \frac{1}{\frac{2 x + 1 - a}{2 x + 1 + a} (1 + z^{2})} \sqrt{\frac{2 x + 1 - a}{2 x + 1 + a}} d z$ $= \frac{2}{2 x + 1 + a} \frac{2 x + 1 + a}{2 x + 1 - a} \sqrt{\frac{2 x + 1 - a}{2 x + 1 + a}} \frac{π}{2} = \frac{π}{2 x + 1 + a} \sqrt{\frac{2 x + 1 + a}{2 x + 1 - a}}$ $= \frac{π}{\sqrt{{(2 x + 1 + a)}^{2} - a^{2}}}$ $c a s e 2 \frac{2 x + 1 - a}{2 x + 1 + a} < 0 \Rightarrow φ (a, x) = \frac{2}{2 x + 1 + a} \int_{0}^{\infty} \frac{d α}{α^{2} - \frac{a - (2 x + 1)}{a + 2 x + 1}}$ $c h a n g e m e n t α = \sqrt{\frac{a - (2 x + 1)}{a + 2 x + 1}} z g i v e$ $φ (a, x) = \frac{2}{2 x + 1 + a} \int_{0}^{\infty} \frac{1}{\frac{a - (2 x + 1)}{a + 2 x + 1} (z^{2} - 1)} \sqrt{\frac{a - (2 x + 1)}{a + (2 x + 1)}} d z$ $= \frac{2}{2 x + 1 + a} \frac{a + 2 x + 1}{a - (2 x + 1)} \sqrt{\frac{a - (2 x + 1)}{a + (2 x + 1)}} \int_{0}^{\infty} \frac{d z}{z^{2} - 1}$ $= \frac{π}{\sqrt{a^{2} - {(2 x + 1)}^{2}}} \frac{1}{2} \int_{0}^{\infty} {\frac{1}{z - 1} - \frac{1}{z + 1}} d z = \frac{π}{2 \sqrt{a^{2} - {(2 x + 1)}^{2}}} {[l n ∣ \frac{z - 1}{z + 1} ∣]}_{0}^{+ \infty} = 0$
Commented by maxmathsup by imad last updated on 17/Sep/18

$2) f o r a = 1 w e g e t \frac{2 x + 1 - a}{2 x + 1 + a} = \frac{2 x}{2 x + 2} = \frac{x}{x + 1}$ $c a s e 1 \frac{x}{x + 1} > 0 \Rightarrow φ (1, x) = \frac{π}{\sqrt{4 {(x + 1)}^{2} - 1}}$ $c a s e 2 \frac{x}{x + 1} < 0 \Rightarrow φ (1, x) = 0$ $a l s o f o r x = 1 w e h a v e \frac{2 x + 1 - a}{2 x + 1 + a} = \frac{3 - a}{3 + a}$ $c a s e 1 \frac{3 - a}{3 + a} > 0 \Rightarrow φ (a, 1) = \frac{π}{\sqrt{{(3 + a)}^{2} - a^{2}}}$ $c a s e 2 \frac{3 - a}{3 + a} < 0 \Rightarrow φ (a, 1) = 0 .$
Commented by maxmathsup by imad last updated on 17/Sep/18

$3) \int_{0}^{\frac{π}{2}} \frac{d t}{2 + 3 {s i n}^{2} t} = φ (3, 2) w e h a v e a = 3 a n d x = 2$ $w e g e t \frac{2 x + 1 - a}{2 x + 1 + a} = \frac{5 - 3}{8} = \frac{1}{4} > 0 \Rightarrow φ (3, 2) = \frac{π}{\sqrt{{(5 + 3)}^{2} - 3^{2}}} = \frac{π}{\sqrt{64 - 9}} = \frac{π}{\sqrt{55}}$
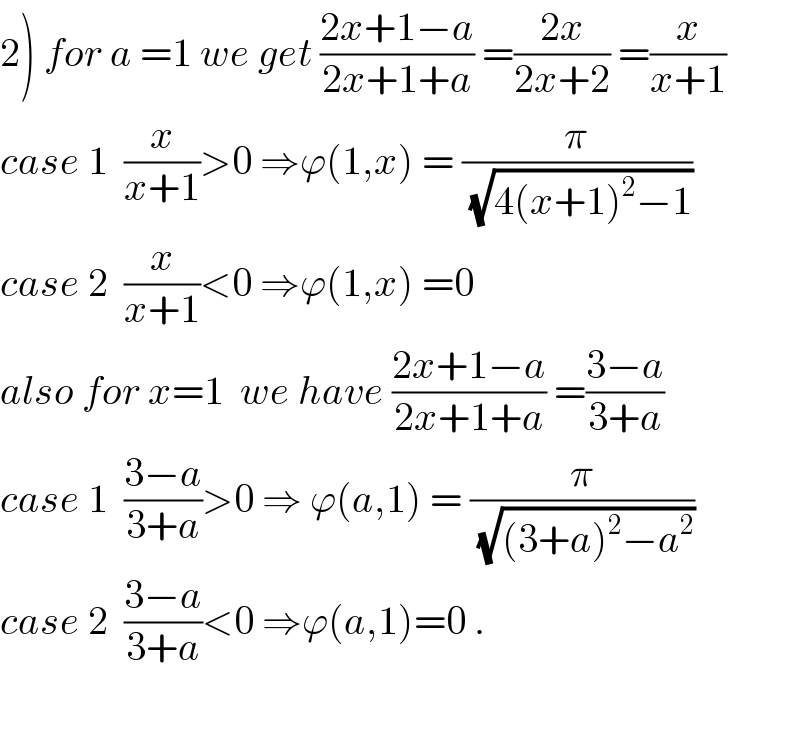
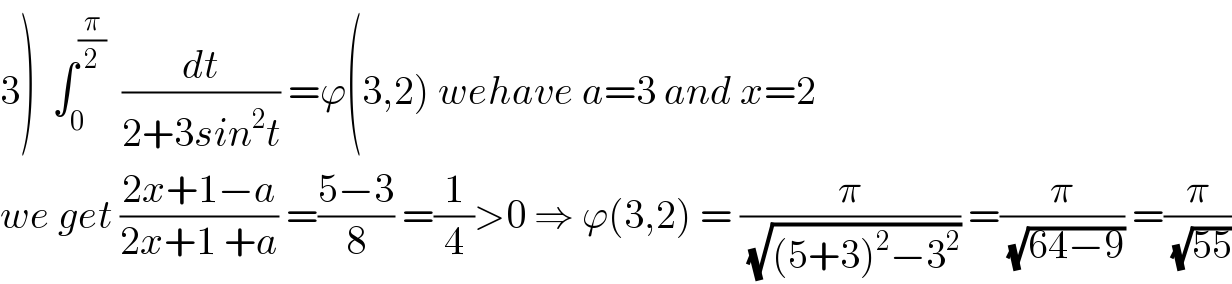
Commented by maxmathsup by imad last updated on 18/Sep/18
$4) we have ϕ(a,x) = ∫_0 ^(π/2) (dt/(x+a sin^2 t)) ⇒ (∂ϕ/∂x)(a,x) =−∫_0 ^(π/2) (dt/((x+asin^2 t)^2 )) ⇒ ∫_0 ^(π/2) (dt/((x +asin^2 t)^2 )) =−(∂ϕ/∂x)(a,x) case 1 ((2x+1−a)/(2x+1+a))>0 ⇒ϕ(a,x) =π{(2x+1+a)^2 −a^2 }^(−(1/2)) ⇒ (∂ϕ/∂x)(a,x) =−(π/2)(4(2x+1+a)){(2x+1+a)^2 −a^2 }^(−(3/2)) = ((2π(2x+1+a))/(((2x+1+a)^2 −a^2 )(√((2x+1+a)^2 −a^2 )))) . case 2 ((zx+1−a)/(2x+1+a))<0 ⇒ϕ(a,x)=0 ⇒ (∂ϕ/∂x)(a,x)=0 .$
$4) w e h a v e φ (a, x) = \int_{0}^{\frac{π}{2}} \frac{d t}{x + a {s i n}^{2} t} \Rightarrow \frac{\partial φ}{\partial x} (a, x) = - \int_{0}^{\frac{π}{2}} \frac{d t}{{(x + {a s i n}^{2} t)}^{2}} \Rightarrow$ $\int_{0}^{\frac{π}{2}} \frac{d t}{{(x + {a s i n}^{2} t)}^{2}} = - \frac{\partial φ}{\partial x} (a, x)$ $c a s e 1 \frac{2 x + 1 - a}{2 x + 1 + a} > 0 \Rightarrow φ (a, x) = π {{(2 x + 1 + a)}^{2} - a^{2}}^{- \frac{1}{2}} \Rightarrow$ $\frac{\partial φ}{\partial x} (a, x) = - \frac{π}{2} (4 (2 x + 1 + a)) {{(2 x + 1 + a)}^{2} - a^{2}}^{- \frac{3}{2}}$ $= \frac{2 π (2 x + 1 + a)}{({(2 x + 1 + a)}^{2} - a^{2}) \sqrt{{(2 x + 1 + a)}^{2} - a^{2}}} .$ $c a s e 2 \frac{z x + 1 - a}{2 x + 1 + a} < 0 \Rightarrow φ (a, x) = 0 \Rightarrow \frac{\partial φ}{\partial x} (a, x) = 0 .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum