
Question and Answers Forum
Question Number 43904 by abdo.msup.com last updated on 17/Sep/18
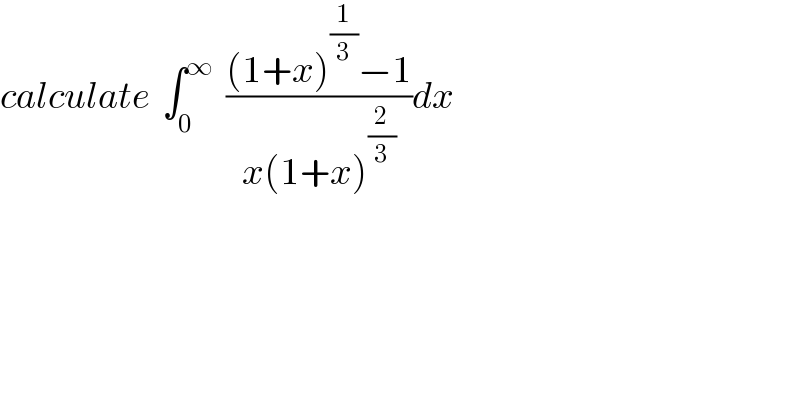
Commented by maxmathsup by imad last updated on 19/Sep/18
![changement (1+x)^(1/3) =t give 1+x =t^3 ⇒ I =∫_1 ^(+∞) ((t−1)/((t^3 −1)t^2 )) (3t^2 )dt = ∫_1 ^(+∞) (3/(t^2 +t +1))dt = ∫_1 ^(+∞) ((3dt)/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (4/3) ∫_(√3) ^(+∞) (3/((1+u^2 )))((√3)/2)du =2(√3) ∫_(√3) ^(+∞) (du/(1+u^2 )) =2(√3)[arctan(u)]_(√3) ^(+∞) =2(√3){(π/2)−(π/3)}=2(√3).(π/6) I = ((π(√3))/3) .](Q43978.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Sep/18

| ||
Question and Answers Forum | ||
Question Number 43904 by abdo.msup.com last updated on 17/Sep/18 | ||
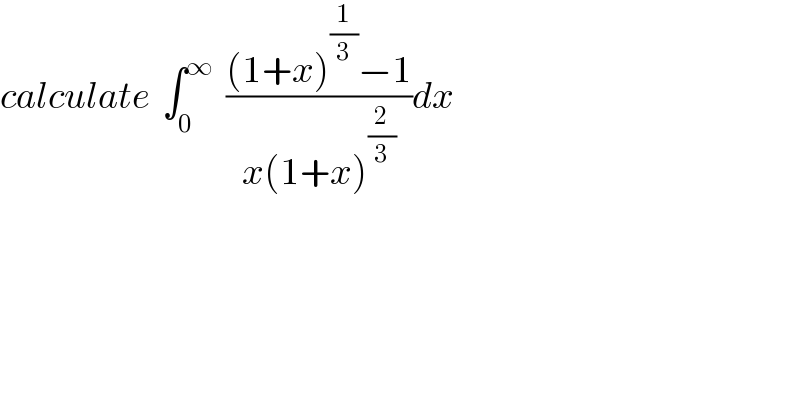 | ||
Commented by maxmathsup by imad last updated on 19/Sep/18 | ||
![changement (1+x)^(1/3) =t give 1+x =t^3 ⇒ I =∫_1 ^(+∞) ((t−1)/((t^3 −1)t^2 )) (3t^2 )dt = ∫_1 ^(+∞) (3/(t^2 +t +1))dt = ∫_1 ^(+∞) ((3dt)/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (4/3) ∫_(√3) ^(+∞) (3/((1+u^2 )))((√3)/2)du =2(√3) ∫_(√3) ^(+∞) (du/(1+u^2 )) =2(√3)[arctan(u)]_(√3) ^(+∞) =2(√3){(π/2)−(π/3)}=2(√3).(π/6) I = ((π(√3))/3) .](Q43978.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Sep/18 | ||
 | ||
| ||