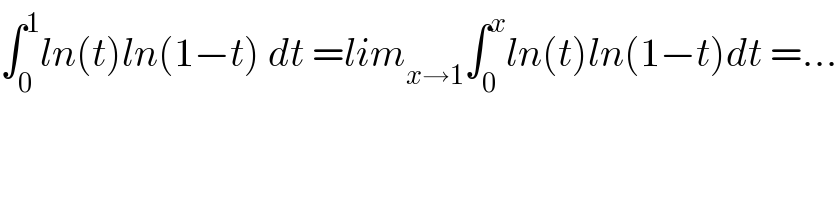1) find f(x) =∫_0 ^x ln(t)ln(1−t)dt with 0≤x≤1 2) find the value of ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 43918 by maxmathsup by imad last updated on 17/Sep/18

$1) f i n d f (x) = \int_{0}^{x} l n (t) l n (1 - t) d t w i t h 0 ⩽ x ⩽ 1$ $2) f i n d t h e v a l u e o f \int_{0}^{1} l n (t) l n (1 - t) d t .$
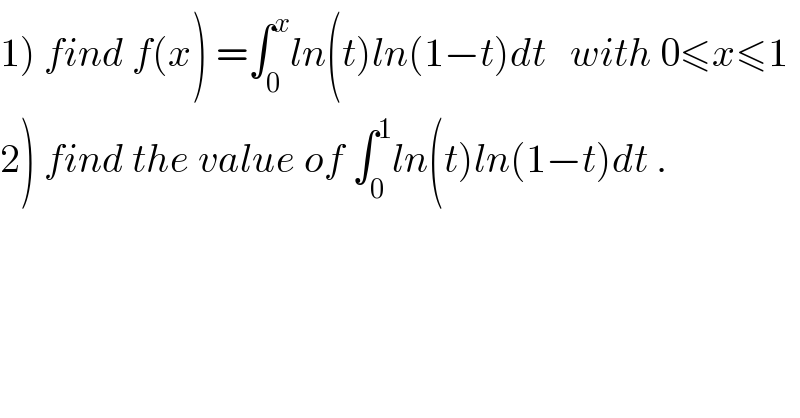
Commented by maxmathsup by imad last updated on 19/Sep/18
$1) we have for 0<t≤x<1 ln^′ (1−t) =−(1/(1−t)) =−Σ_(n=0) ^∞ t^n ⇒ ln(1−t) =−Σ_(n=0) ^∞ (1/(n+1))t^(n+1) =−Σ_(n=1) ^∞ (t^n /n) ⇒ f(x) =−∫_0 ^x ln(t)(Σ_(n=1) ^∞ (t^n /n))dt =−Σ_(n=1) ^∞ (1/n) ∫_0 ^x t^n ln(t) dt by parts A_n (x)= ∫_0 ^x t^n ln(t)dt =[(1/(n+1))t^(n+1) ln(t)]_0 ^x −∫_0 ^x (1/(n+1))t^(n+1) (dt/t) =(1/(n+1)) x^(n+1) ln(x) −(1/(n+1))∫_0 ^x t^n dt = (1/(n+1))x^(n+1) ln(x)−(1/((n+1)^2 )) x^(n+1) ⇒ f(x) =−Σ_(n=1) ^∞ (1/n){ (1/(n+1)) x^(n+1) ln(x)−(1/((n+1)^2 )) x^(n+1) } = −Σ_(n=1) ^∞ (1/(n(n+1))) x^(n+1) ln(x) +Σ_(n=1) ^∞ (1/(n(n+1)^2 )) x^(n+1) =H(x)−K(x) K(x) =ln(x) Σ_(n=1) ^∞ {(1/n)−(1/(n+1))}x^(n+1) =ln(x)Σ_(n=1) ^∞ (x^(n+1) /n) −ln(x)Σ_(n=1) ^∞ (x^(n+1) /(n+1)) =xln(x) Σ_(n=1) ^∞ (x^n /n) −ln(x) Σ_(n=2) ^∞ (x^n /n) =−xln(x)ln(1−x) −ln(x)(−ln∣1−x∣−x) =−xln(x)ln∣1−x∣+ln(x)(ln∣1−x∣ +x) =(1−x)ln(x)ln∣1−x∣ +xln(x) .also we have (d/dx)K(x) =Σ_(n=1) ^∞ (1/(n(n+1))) x^n =Σ_(n=1) ^∞ {(1/n)−(1/(n+1))}x^n =Σ_(n=1) ^∞ (x^n /n) −Σ_(n=1) ^∞ (x^n /(n+1)) =−ln∣1−x∣−Σ_(n=2) ^∞ (x^(n−1) /n) =−ln∣1−x∣ −(1/x) {Σ_(n=1) ^∞ (x^n /n) −x} =−ln∣1−x∣+(1/x)ln∣1−x) +1 =((1/x)−1)ln∣1−x∣ +1 =(((1−x)ln∣1−x∣)/x) +1 ⇒ K(x) = x + ∫ (((1−x)ln∣1−x∣)/x) dx +k ....be continued...$
$1) w e h a v e f o r 0 < t ⩽ x < 1 {l n}^{^{'}} (1 - t) = - \frac{1}{1 - t} = - \sum_{n = 0}^{\infty} t^{n} \Rightarrow$ $l n (1 - t) = - \sum_{n = 0}^{\infty} \frac{1}{n + 1} t^{n + 1} = - \sum_{n = 1}^{\infty} \frac{t^{n}}{n} \Rightarrow$ $f (x) = - \int_{0}^{x} l n (t) (\sum_{n = 1}^{\infty} \frac{t^{n}}{n}) d t = - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{x} t^{n} l n (t) d t$ $b y p a r t s A_{n} (x) = \int_{0}^{x} t^{n} l n (t) d t = {[\frac{1}{n + 1} t^{n + 1} l n (t)]}_{0}^{x} - \int_{0}^{x} \frac{1}{n + 1} t^{n + 1} \frac{d t}{t}$ $= \frac{1}{n + 1} x^{n + 1} l n (x) - \frac{1}{n + 1} \int_{0}^{x} t^{n} d t = \frac{1}{n + 1} x^{n + 1} l n (x) - \frac{1}{{(n + 1)}^{2}} x^{n + 1} \Rightarrow$ $f (x) = - \sum_{n = 1}^{\infty} \frac{1}{n} {\frac{1}{n + 1} x^{n + 1} l n (x) - \frac{1}{{(n + 1)}^{2}} x^{n + 1}}$ $= - \sum_{n = 1}^{\infty} \frac{1}{n (n + 1)} x^{n + 1} l n (x) + \sum_{n = 1}^{\infty} \frac{1}{n {(n + 1)}^{2}} x^{n + 1} = H (x) - K (x)$ $K (x) = l n (x) \sum_{n = 1}^{\infty} {\frac{1}{n} - \frac{1}{n + 1}} x^{n + 1}$ $= l n (x) \sum_{n = 1}^{\infty} \frac{x^{n + 1}}{n} - l n (x) \sum_{n = 1}^{\infty} \frac{x^{n + 1}}{n + 1}$ $= x l n (x) \sum_{n = 1}^{\infty} \frac{x^{n}}{n} - l n (x) \sum_{n = 2}^{\infty} \frac{x^{n}}{n}$ $= - x l n (x) l n (1 - x) - l n (x) (- l n ∣ 1 - x ∣ - x)$ $= - x l n (x) l n ∣ 1 - x ∣ + l n (x) (l n ∣ 1 - x ∣ + x)$ $= (1 - x) l n (x) l n ∣ 1 - x ∣ + x l n (x) . a l s o w e h a v e$ $\frac{d}{d x} K (x) = \sum_{n = 1}^{\infty} \frac{1}{n (n + 1)} x^{n} = \sum_{n = 1}^{\infty} {\frac{1}{n} - \frac{1}{n + 1}} x^{n}$ $= \sum_{n = 1}^{\infty} \frac{x^{n}}{n} - \sum_{n = 1}^{\infty} \frac{x^{n}}{n + 1} = - l n ∣ 1 - x ∣ - \sum_{n = 2}^{\infty} \frac{x^{n - 1}}{n}$ $= - l n ∣ 1 - x ∣ - \frac{1}{x} {\sum_{n = 1}^{\infty} \frac{x^{n}}{n} - x} = - l n ∣ 1 - x ∣ + \frac{1}{x} l n ∣ 1 - x) + 1$ $= (\frac{1}{x} - 1) l n ∣ 1 - x ∣ + 1 = \frac{(1 - x) l n ∣ 1 - x ∣}{x} + 1 \Rightarrow$ $K (x) = x + \int \frac{(1 - x) l n ∣ 1 - x ∣}{x} d x + k . . . . b e c o n t i n u e d . . .$
Commented by maxmathsup by imad last updated on 19/Sep/18
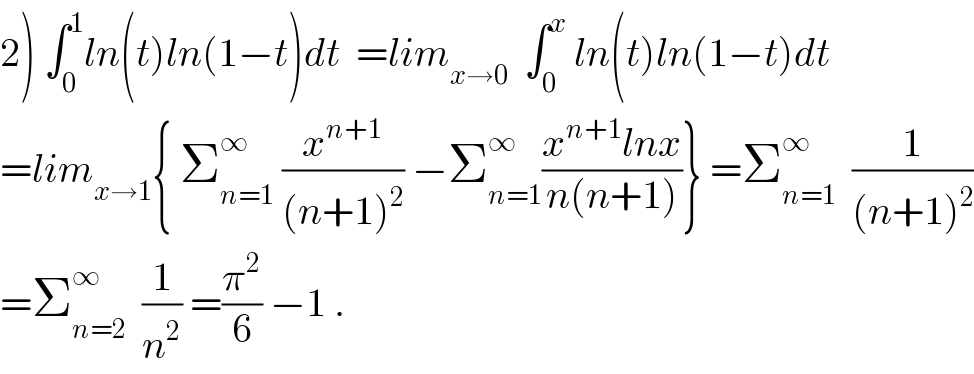
$2) ∫_0 ^1 ln(t)ln(1−t)dt =lim_(x→0) ∫_0 ^x ln(t)ln(1−t)dt =lim_(x→1) { Σ_(n=1) ^∞ (x^(n+1) /((n+1)^2 )) −Σ_(n=1) ^∞ ((x^(n+1) lnx)/(n(n+1)))} =Σ_(n=1) ^∞ (1/((n+1)^2 )) =Σ_(n=2) ^∞ (1/n^2 ) =(π^2 /6) −1 .$
$2) \int_{0}^{1} l n (t) l n (1 - t) d t = {l i m}_{x \to 0} \int_{0}^{x} l n (t) l n (1 - t) d t$ $= {l i m}_{x \to 1} {\sum_{n = 1}^{\infty} \frac{x^{n + 1}}{{(n + 1)}^{2}} - \sum_{n = 1}^{\infty} \frac{x^{n + 1} l n x}{n (n + 1)}} = \sum_{n = 1}^{\infty} \frac{1}{{(n + 1)}^{2}}$ $= \sum_{n = 2}^{\infty} \frac{1}{n^{2}} = \frac{π^{2}}{6} - 1 .$
Commented by maxmathsup by imad last updated on 19/Sep/18

$\int_{0}^{1} l n (t) l n (1 - t) d t = {l i m}_{x \to 1} \int_{0}^{x} l n (t) l n (1 - t) d t = . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum