Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 43934 by abdo.msup.com last updated on 18/Sep/18

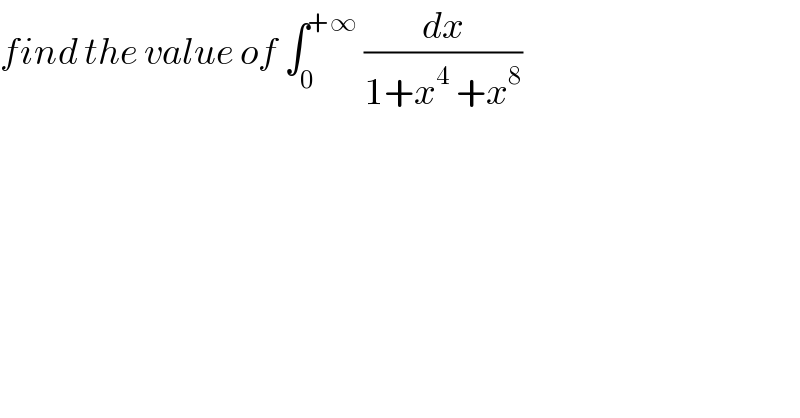
find the value of ∫_0 ^(+∞) (dx/(1+x^4 +x^8 ))

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} \:+{x}^{\mathrm{8}} } \\ $$

Commented by maxmathsup by imad last updated on 19/Sep/18

let I = ∫_0 ^∞ (dx/(1+x^4 +x^8 )) we have 2I =∫_(−∞) ^(+∞) (dx/(1+x^4 +x^8 )) let ϕ(z) =(1/(z^8 +z^4 +1)) .poles of ϕ? z^4 =t ⇒t^2 +t +1=0 ⇒t=j or t=j^− ⇒ z^4 =j ⇒z^4 =e^((i2π)/3) ⇒ϕ(z)= (1/((z^4 −j)(z^4 +j))) =(1/((z^2 −(√j))(z^2 +(√(j)))(z^2 −(√(−j)))(z^2 +(√(−j))))) = (1/((z^2 −e^((iπ)/3) )(z^2 +e^((iπ)/3) )(z^2 −e^(−((iπ)/3)) )(z^2 +e^(−((iπ)/3)) ))) = (1/((z−e^((iπ)/6) )(z+e^((iπ)/6) )(z−ie^((iπ)/6) )(z+i e^((iπ)/6) )(z −e^(−((iπ)/6)) )(z+e^(−((iπ)/6)) )(z−ie^(−((iπ)/6)) )(z+i e^(−((iπ)/6)) ))) the poles of ϕ are +^− e^((iπ)/6) ,+^− i e^((iπ)/6) ,+^− e^(−((iπ)/6)) ,+^− i e^(−((iπ)/6)) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ {Res(ϕ,e^((iπ)/6) ) +Res(ϕ,i e^((iπ)/6) ) +Res(ϕ,−e^(−((iπ)/6)) ) +Res(ϕ,−ie^(−((iπ)/6)) )} we have f(x)=(1/(p(x))) ⇒ Res(ϕ ,z_i )=(1/(p^′ (z_i ))) ⇒ Res(ϕ,e^((iπ)/6) )= (1/(8 (e^((iπ)/6) )^7 +4(e^((iπ)/6) )^3 )) = (1/(8 e^(i((7π)/6)) + 4i)) =(1/(−8 e^((iπ)/6) +4i)) Res(ϕ,i e^((iπ)/6) ) = (1/(8 (i e^((iπ)/6) )^7 +4(i e^((iπ)/6) )^3 )) = (1/(−8i (−e^((iπ)/6) )−4i(i))) =(1/(8i e^((iπ)/6) +4)) Res(ϕ,−e^(−((iπ)/6)) ) = (1/(8(−e^(−((iπ)/6)) )^7 +4(−e^(−((iπ)/6)) )^3 )) = (1/(−8(−1) e^(−((iπ)/6)) −4(−i))) =(1/(8 e^(−((iπ)/6)) +4i)) Res(ϕ,−i e^(−i(π/6)) ) = (1/(8(−i e^(−((iπ)/6)) )^7 +4 (−i e^((iπ)/6) )^3 )) ...be continued...

$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} \:+{x}^{\mathrm{8}} }\:\:{we}\:{have}\:\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} \:+{x}^{\mathrm{8}} }\:\:{let} \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{8}} \:+{z}^{\mathrm{4}} +\mathrm{1}}\:\:.{poles}\:{of}\:\varphi?\:{z}^{\mathrm{4}} ={t}\:\Rightarrow{t}^{\mathrm{2}} +{t}\:+\mathrm{1}=\mathrm{0}\:\Rightarrow{t}={j}\:{or}\:{t}=\overset{−} {{j}}\:\Rightarrow \\ $$$${z}^{\mathrm{4}} ={j}\:\Rightarrow{z}^{\mathrm{4}} ={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left({z}\right)=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{4}} −{j}\right)\left({z}^{\mathrm{4}} \:+{j}\right)}\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −\sqrt{{j}}\right)\left({z}^{\mathrm{2}} +\sqrt{\left.{j}\right)}\left({z}^{\mathrm{2}} −\sqrt{−{j}}\right)\left({z}^{\mathrm{2}} \:+\sqrt{−{j}}\right)\right.} \\ $$$$=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} \:+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} \:−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} \:+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\:\frac{\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}−{ie}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}\:−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}−{ie}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{i}\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)} \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{6}}} ,\overset{−} {+}{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:,\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{6}}} \:,\overset{−} {+}{i}\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\:+{Res}\left(\varphi,{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\:+{Res}\left(\varphi,−{ie}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\right\} \\ $$$${we}\:{have}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{p}\left({x}\right)}\:\Rightarrow\:{Res}\left(\varphi\:,{z}_{{i}} \right)=\frac{\mathrm{1}}{{p}^{'} \left({z}_{{i}} \right)}\:\Rightarrow \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)=\:\frac{\mathrm{1}}{\mathrm{8}\:\left({e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{7}} \:+\mathrm{4}\left({e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}\:{e}^{{i}\frac{\mathrm{7}\pi}{\mathrm{6}}} \:+\:\mathrm{4}{i}}\:=\frac{\mathrm{1}}{−\mathrm{8}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:+\mathrm{4}{i}} \\ $$$${Res}\left(\varphi,{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{8}\:\left({i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{7}} \:+\mathrm{4}\left({i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{−\mathrm{8}{i}\:\left(−{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)−\mathrm{4}{i}\left({i}\right)}\:=\frac{\mathrm{1}}{\mathrm{8}{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:+\mathrm{4}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{8}\left(−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{7}} \:+\mathrm{4}\left(−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{−\mathrm{8}\left(−\mathrm{1}\right)\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \:−\mathrm{4}\left(−{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \:+\mathrm{4}{i}} \\ $$$${Res}\left(\varphi,−{i}\:{e}^{−{i}\frac{\pi}{\mathrm{6}}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{8}\left(−{i}\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{7}} \:+\mathrm{4}\:\left(−{i}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} }\:...{be}\:{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com