
Question and Answers Forum
Question Number 43939 by abdo.msup.com last updated on 18/Sep/18
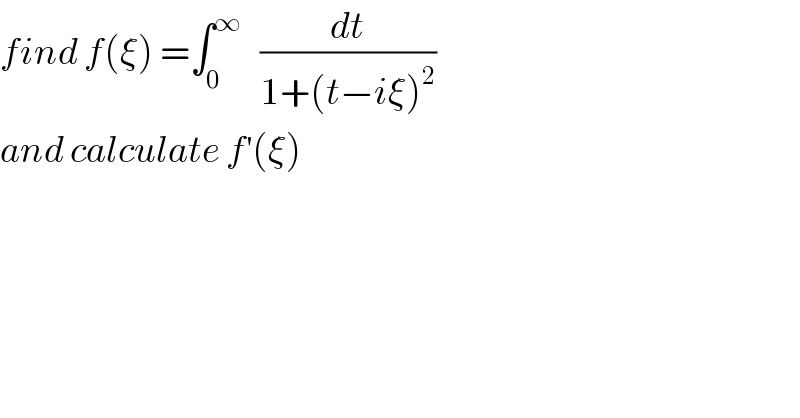
Commented by maxmathsup by imad last updated on 22/Sep/18
![f(ξ) =∫_0 ^∞ (dt/((t−ξ)^2 −i^2 )) =∫_0 ^∞ (dt/(((t−ξ)−i)(t−ξ +i))) =(1/(2i))∫_0 ^∞ { (1/(t−ξ−i)) −(1/(t−ξ +i))}dt ⇒2i f(ξ) =∫_0 ^∞ (dt/(t−ξ−i)) −∫_0 ^∞ (dt/(t−ξ +i)) but ∫ (dt/(t−ξ−i)) =∫ ((t−ξ +i)/((t−ξ)^2 +1)) dt =∫ ((t−ξ)/((t−ξ)^2 +1))dt +i ∫ (dt/((t−ξ)^2 +1)) ∫ ((t−ξ)/((t−ξ)^2 +1))dt =(1/2)ln{ (t−ξ)^2 +1} +c_1 ∫ (dt/((t−ξ)^2 +1)) =_(t−ξ =u) ∫ (du/(1+u^2 )) =arctan(t−ξ) +c_2 ⇒ ∫ (dt/(t−ξ−i)) =(1/2)ln{(t−ξ)^2 +1} +i arctan(t−ξ) +c also ∫ (dt/(t−ξ +i)) = (1/2)ln{(t−ξ)^2 +1}−i arctan(t−ξ) ⇒ 2if(ξ)= 2i [arctan(t−ξ)]_0 ^(+∞) = 2i{ (π/2) +arctan(ξ)} ⇒ f(ξ) =(π/2) +arctan(ξ) and we have f^′ (ξ) = (1/(1+ξ^2 )) .](Q44163.png)
| ||
Question and Answers Forum | ||
Question Number 43939 by abdo.msup.com last updated on 18/Sep/18 | ||
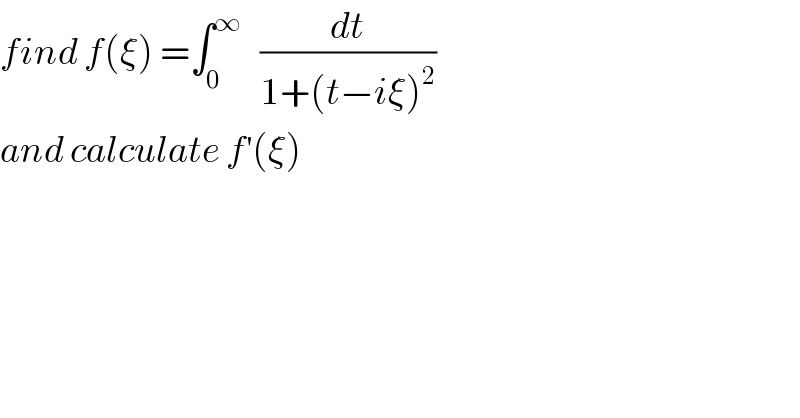 | ||
Commented by maxmathsup by imad last updated on 22/Sep/18 | ||
![f(ξ) =∫_0 ^∞ (dt/((t−ξ)^2 −i^2 )) =∫_0 ^∞ (dt/(((t−ξ)−i)(t−ξ +i))) =(1/(2i))∫_0 ^∞ { (1/(t−ξ−i)) −(1/(t−ξ +i))}dt ⇒2i f(ξ) =∫_0 ^∞ (dt/(t−ξ−i)) −∫_0 ^∞ (dt/(t−ξ +i)) but ∫ (dt/(t−ξ−i)) =∫ ((t−ξ +i)/((t−ξ)^2 +1)) dt =∫ ((t−ξ)/((t−ξ)^2 +1))dt +i ∫ (dt/((t−ξ)^2 +1)) ∫ ((t−ξ)/((t−ξ)^2 +1))dt =(1/2)ln{ (t−ξ)^2 +1} +c_1 ∫ (dt/((t−ξ)^2 +1)) =_(t−ξ =u) ∫ (du/(1+u^2 )) =arctan(t−ξ) +c_2 ⇒ ∫ (dt/(t−ξ−i)) =(1/2)ln{(t−ξ)^2 +1} +i arctan(t−ξ) +c also ∫ (dt/(t−ξ +i)) = (1/2)ln{(t−ξ)^2 +1}−i arctan(t−ξ) ⇒ 2if(ξ)= 2i [arctan(t−ξ)]_0 ^(+∞) = 2i{ (π/2) +arctan(ξ)} ⇒ f(ξ) =(π/2) +arctan(ξ) and we have f^′ (ξ) = (1/(1+ξ^2 )) .](Q44163.png) | ||