
Question and Answers Forum
Question Number 44002 by maxmathsup by imad last updated on 19/Sep/18
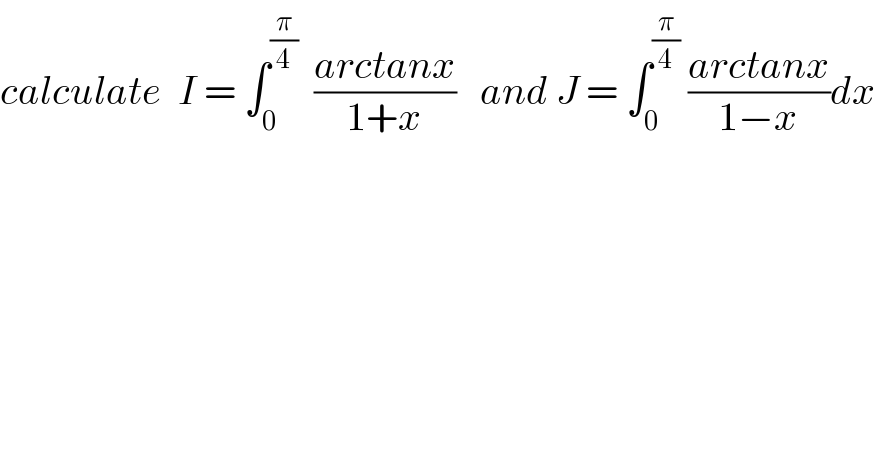
Commented by maxmathsup by imad last updated on 24/Sep/18
![let f(α) =∫_0 ^(π/4) ((arctan(αx))/(1+x))dx ⇒I =f(1) we have f^′ (α) = ∫_0 ^(π/4) ((x dx)/((1+x)(1+α^2 x^2 ))) =_(αx =t) ∫_0 ^((απ)/4) ((tdt)/(α(1+(t/α))(1+t^2 ))) = ∫_0 ^((απ)/4) ((tdt)/((t+α)(t^2 +1))) let decompose F(t) = (t/((t+α)(t^2 +1))) F(t) = (a/(t+α)) +((bt +c)/(t^2 +1)) we have a=lim_(t→−α) (t+α)F(t)=((−α)/(1+α^2 )) lim_(t→+∞) t F(t) =0 =a+b ⇒b =(α/(1+α^2 )) ⇒F(t)=−(α/((1+α^2 )(t+α))) +(((α/(1+α^2 ))t +c)/(1+t^2 )) F(0)=0 = −(α/((1+α^2 )α)) +c ⇒c =(1/(1+α^2 )) ⇒ F(t) = −(α/((1+α^2 )(t+α))) +(1/(1+α^2 )) ((αt +1)/(t^2 +1)) ⇒ f^′ (α) =((−α)/(1+α^2 )) ∫_0 ^((απ)/4) (dt/(t+α)) +(1/(1+α^2 )) ∫_0 ^((απ)/4) ((αt +1)/(t^(2 ) +1))dt but ∫_0 ^((απ)/4) (dt/(t+α)) =[ln∣t+α∣]_0 ^((απ)/4) =ln∣((απ)/4)+α∣−ln∣α∣ =ln∣1+(π/4)∣ ∫_0 ^((απ)/4) ((αt +1)/(t^2 +1)) dt =(α/2)[ln(t^2 +1)]_0 ^((απ)/4) +arctan(((απ)/4)) =(α/2)ln(1+((α^2 π^2 )/(16))) +arctan(((απ)/4)) ⇒ f^′ (α) =((−α)/(1+α^2 ))ln(1+(π/4)) + (α/(2(1+α^2 )))ln(1+((α^2 π^2 )/(16))) +(1/(1+α^2 ))arctan(((απ)/4)) ⇒ f(α) =−ln(1+(π/4)) ∫_0 ^α (x/(1+x^2 ))dx +(1/2) ∫_0 ^α (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^α (1/(1+x^2 ))arctan(((πx)/4))dx +c ( c=f(0)=0) ⇒ f(1) =−ln(1+(π/4)) ∫_0 ^1 (x/(1+x^2 ))dx +(1/2) ∫_0 ^1 (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^1 ((arctan(((πx)/4)))/(1+x^2 ))dx ....be continued...](Q44246.png)
| ||
Question and Answers Forum | ||
Question Number 44002 by maxmathsup by imad last updated on 19/Sep/18 | ||
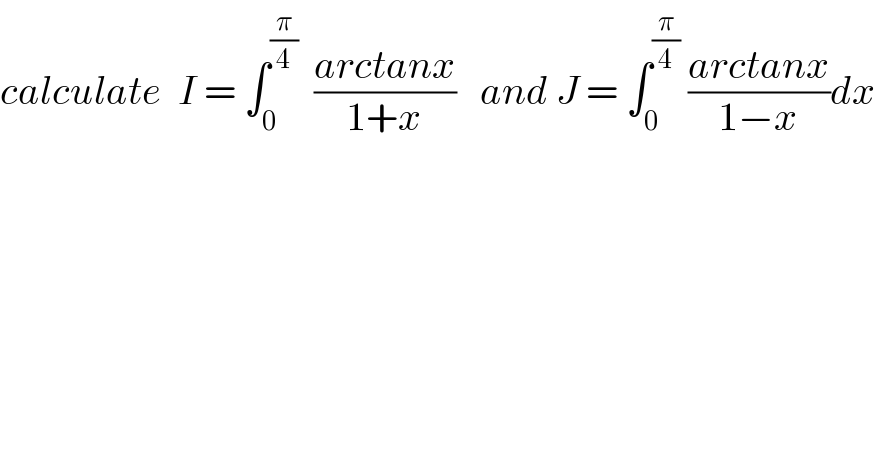 | ||
Commented by maxmathsup by imad last updated on 24/Sep/18 | ||
![let f(α) =∫_0 ^(π/4) ((arctan(αx))/(1+x))dx ⇒I =f(1) we have f^′ (α) = ∫_0 ^(π/4) ((x dx)/((1+x)(1+α^2 x^2 ))) =_(αx =t) ∫_0 ^((απ)/4) ((tdt)/(α(1+(t/α))(1+t^2 ))) = ∫_0 ^((απ)/4) ((tdt)/((t+α)(t^2 +1))) let decompose F(t) = (t/((t+α)(t^2 +1))) F(t) = (a/(t+α)) +((bt +c)/(t^2 +1)) we have a=lim_(t→−α) (t+α)F(t)=((−α)/(1+α^2 )) lim_(t→+∞) t F(t) =0 =a+b ⇒b =(α/(1+α^2 )) ⇒F(t)=−(α/((1+α^2 )(t+α))) +(((α/(1+α^2 ))t +c)/(1+t^2 )) F(0)=0 = −(α/((1+α^2 )α)) +c ⇒c =(1/(1+α^2 )) ⇒ F(t) = −(α/((1+α^2 )(t+α))) +(1/(1+α^2 )) ((αt +1)/(t^2 +1)) ⇒ f^′ (α) =((−α)/(1+α^2 )) ∫_0 ^((απ)/4) (dt/(t+α)) +(1/(1+α^2 )) ∫_0 ^((απ)/4) ((αt +1)/(t^(2 ) +1))dt but ∫_0 ^((απ)/4) (dt/(t+α)) =[ln∣t+α∣]_0 ^((απ)/4) =ln∣((απ)/4)+α∣−ln∣α∣ =ln∣1+(π/4)∣ ∫_0 ^((απ)/4) ((αt +1)/(t^2 +1)) dt =(α/2)[ln(t^2 +1)]_0 ^((απ)/4) +arctan(((απ)/4)) =(α/2)ln(1+((α^2 π^2 )/(16))) +arctan(((απ)/4)) ⇒ f^′ (α) =((−α)/(1+α^2 ))ln(1+(π/4)) + (α/(2(1+α^2 )))ln(1+((α^2 π^2 )/(16))) +(1/(1+α^2 ))arctan(((απ)/4)) ⇒ f(α) =−ln(1+(π/4)) ∫_0 ^α (x/(1+x^2 ))dx +(1/2) ∫_0 ^α (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^α (1/(1+x^2 ))arctan(((πx)/4))dx +c ( c=f(0)=0) ⇒ f(1) =−ln(1+(π/4)) ∫_0 ^1 (x/(1+x^2 ))dx +(1/2) ∫_0 ^1 (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^1 ((arctan(((πx)/4)))/(1+x^2 ))dx ....be continued...](Q44246.png) | ||